�u���ʉ��v
�@���ϗʉ�͂́u�d��A���́v�u���ʕ��́v�u�听�����́v���́A�ʓI�f�[�^���������͕��@�ł��邪�A�����ʓI�f�[�^�̌`�ŕW�{����Ƃ͌���Ȃ��B�����ŁA����ꂽ���I�f�[�^�ɓK���Ȑ��ʂ�^���A���I�f�[�^�𐔗ʉ����邱�Ƃɂ�葽�ϗʉ�͂��s����悤�ɂ��邱�Ƃ��u���ʉ��v�Ƃ����B
�@���v�ň����f�[�^�ɂ́A�u�ʓI�f�[�^�v�Ɓu���I�f�[�^�v������A�ʓI�f�[�^�͐��l�̊Ԋu�ɈӖ������f�[�^�ł��邪�A���I�f�[�^�͂��̊Ԋu�ɈӖ��͂����Ȃ����̂��̂Ƌ�ʂ�����A�������������肷��f�[�^�ł���B
![]()
![]() �ʓI�f�[�^ �@�@
�Ԋu�ړx�c��Ό��_�������Ȃ��ړx�f�[�^
�ʓI�f�[�^ �@�@
�Ԋu�ړx�c��Ό��_�������Ȃ��ړx�f�[�^
�@�@�@�@�@�@�@�@�@�@�@�@���ړx�c��Ό��_�����ړx�f�[�^
![]() �@�@�@���I�f�[�^�@�@�@�@���`�ړx�c���ނ������f�[�^�ő召�W�ɈӖ��͎����Ȃ�
�@�@�@���I�f�[�^�@�@�@�@���`�ړx�c���ނ������f�[�^�ő召�W�ɈӖ��͎����Ȃ�
�@�@�@�@�@�@�@�@�@�@�@�@�����ړx�c�����W�̑召�ɈӖ������f�[�^
�@�ʏ펿�I�f�[�^�͌v�Z���邱�Ƃ��ł��Ȃ��̂ŁA���̂܂ܓ��v���͂����邱�Ƃ͂ł��Ȃ��B�����ŁA���I�f�[�^��ړI�ɍ����悤�ɍœK�Ȑ��l�ɒu�������Đ��ʉ����邱�Ƃɂ��A���ϗʓI�ȉ�͂��ł���悤�ɂ���̂����ʉ��ł���A�u�d��A���́v�u���ʕ��́v�u�听�����́v�ɑΉ�����̂��A�u���ʉ��T�ށv�u���ʉ��U�ށv�u���ʉ��V�ށv�ł���B
�X�D�@���ʉ��T��
���ʉ��T�ނ́A�ʓI�f�[�^�͂���d��A���͂ɑΉ����鎿�I�f�[�^�͂�����@�Ł@�@�@����B�d��A���͂ł́A�ʓI�f�[�^�ł�������ϗʂ���A�ʓI�f�[�^�ł���ړI�ϗʂ�\�������B����ɑ����ʉ��T�ނł́A�A�C�e���E�J�f�S���ƌĂ�鎿�I�f�[�^�āA���̒l����ʓI�f�[�^�ł���O�I��i�ړI�ϗʂɑΉ�����j����@�ł���B
�A�C�e���i���ځj�Ƃ͎��⎖���̂悤�Ȃ��̂ł���A�J�e�S���Ƃ͂��̉̂悤�Ȃ��̂ł���B
�@�A�C�e���́A�Ⴆ�u�M���͉p�ꂪ�D���ł����H�v�̂悤�ɃA���P�[�g�̎��⎖���̂悤�ɗ^�����A�J�e�S���́u�͂��^�������v�̂悤�ɕ��ނŗ^������B���̎��I�f�[�^�ł���J�e�S������O�I��ƌĂ��ʓI�f�[�^��\������̂����ʉ��T�ނƂ������͕��@�ł���B
�X�D�P�@�\�����`�������߂�B
9.1.1�A�C�e�����P�A�J�e�S�����Q�̏ꍇ���l����B
|
�W�{�m�� |
�O�I� |
�A�@�C�@�e�@�� |
|
|
�J�e�S���P |
�J�e�S���Q |
||
|
�P �Q �c �� |
��1 ��2 �c ��n |
��11 ��12 �c ��1n |
��21 ��22 �c ��2n |
���܁A�O�I��Ƃ��ĉp��̓_���i�P�O�_���_�j�A�A�C�e���Ƃ��āu�p��͍D���ł����H�v�Ƃ������⎖���A�J�e�S���Ƃ��āu�͂��^�������v�Ƃ���B
|
�W�{�m�� |
�O�I� |
�p��͍D���ł����H |
|
|
�͂� |
������ |
||
|
�P �Q �R �S �T �U �V �W |
�Q �S �T �V �W �U �T �R |
� � � � |
� � � � |
�A���P�[�g���Ƃ������ʁA�Y������J�e�S����ڈ�����āA��̂悤�ȕ\���Ƃ���B
���ɁA�J�e�S���ɂ����āA�Y��������uځv���������A���̂܂܂ł͌v�Z���邱�Ƃ��ł��Ȃ��̂Łu�Y���L��c�P�v�u�Y�������c�O�v�ƒu��������B���̒u��������ϐ��̂��Ƃ��u�_�~�[�ϐ��v�ƌ����B
![]() �@�@�@�@�@�@�P�c�A�C�e��(i)�A�J�e�S��(j)�ŊY���L��
�@�@�@�@�@�@�P�c�A�C�e��(i)�A�J�e�S��(j)�ŊY���L��
�@ �_�~�[�ϐ��i��ij�j
�@�@�@�@�@�@�O�c�A�C�e��(i)�A�J�e�S��(j)�ŊY���Ȃ�
���̃_�~�[�ϐ����g�p���āA��قǂ̕\�𐔗ʉ����Ă݂��
|
�W�{�m�� |
�O�I� �� |
�p��͍D���ł����H |
|
|
�͂� (��1) |
������(��2) |
||
|
�P �Q �R �S �T �U �V �W |
�Q �S �T �V �W �U �T �R |
�O �O �P �P �P �P �O �O |
�P �P �O �O �O �O �P �P |
�A�C�e���E�J�e�S���̌��ʂ���A�O�I������߂�\�����x���l����B
�x����1���1�{��2���1 �Ƃ����
![]() �\���l�� �x1����1��O�{��2��P
�\���l�� �x1����1��O�{��2��P
�@�@�@�@�@�@
�x2����1��O�{��2��P
�@�@�@�@�@�@
�x3����1��P�{��2��O
�@�@�@�@�@�@
�x4����1��P�{��2��O
�@�@�@�@�@�@ �x5����1��P�{��2��O
�@�@�@�@�@�@�x6����1��P�{��2��O
�@�@�@�@�@�@ �x7����1��O�{��2��P
�@�@�@�@�@�@�x8����1��O�{��2��P
�\���l�xi�Ǝ����l��i �Ƃ̂�����������������̂ŁA�ŏ��Q��@���g����
�@�@���i��i�|�xi�j2 ���ŏ��ɂ��邱�Ƃ��l����B
�@�@���i��i�|�xi�j2 =(2�|a2)2+(4�|a2)2�{(5�|a1)2�{(7�|a1)2�{(8�|a1)2�{(6�|a1)2�{(5�|a2)2�{(3�|a2)2
= 4a12 �{ 4a22 �| 52a1 �| 28a2 �{ 228 ���f�Ƃ���
�@�@���̂f����1��2 �ŕΔ������O�Ƃ����āA���K���������
![]() ����āA�\�����x�́A�x��6.5���11 �{ 3.5��12 �ƂȂ�B
����āA�\�����x�́A�x��6.5���11 �{ 3.5��12 �ƂȂ�B
���̎����g�p���邱�Ƃɂ��A�A���P�|�g���ʂ���O�I��ł���p��̓_����\�����邱�@�@�Ƃ��ł���B
9.1.2�@�A�C�e�����Q�A�J�e�S�����Q�̎�
�i�P�j�A�C�e�����P�̎��Ɠ����悤�ɍŏ��Q��@�ŗ\���������߂�B
�@�@�@���x�̓A�C�e�����Q�A�p��Ɛ��w�B�J�e�S�����Q�A�D���ƌ����̏ꍇ���l����B
|
�W�{No |
�p��̓_�� �� |
�p�@�� |
���@�w |
||
|
�D�� ��11 |
���� ��12 |
�D�� ��21 |
���� ��22 |
||
|
�P �Q �R �S �T �U �V �W |
�Q �S �T �V �W �U �T �R |
� � � � |
� � � � |
� � � � |
� � � � |
������_�~�[�ϐ����g�p���ď�����
|
�W�{No |
�p��̓_�� |
�p�@�� |
���@�w |
||
|
�D�� |
���� |
�D�� |
���� |
||
|
�P �Q �R �S �T �U �V �W |
�Q �S �T �V �W �U �T �R |
�O �O �P �P �P �O �P �O |
�P �P �O �O �O �P �O �P |
�O �P �P �O �P �P �O �O |
�P �O �O �P �O �O �P �P |
�����ŗ\�����x��
�@�@�@�x����11���11�{��12���12�{��21���21�{��22���22 �Ƃ���B
�A�C�e�����P�̎��Ɠ��l�ɂ���
���i��i�|�xi�j2 ���f�Ƃ��āA���̎�����11���12���21���22 �ŕΔ������ĂO�Ƃ����A���K��������B
�f��(2�|��12�|��22)2 �{ (4�|��12�|��21)2 �{
�c
�{ (3�|��12�|��22)2
��228�|50��11�|30��12�|46��21�|34��22�{4��11���21�{4��11���22�{4��12���21�{4��12���22�{4��112�{4��122�{4��212�{4��222
�@�@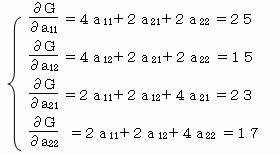
�_�~�|�ϐ��ԂŁA��11�{��12���P ��21�{��22���P �ƂȂ��Ă��邽�߂ɁA���̂܂܂ł�
�@�@��ij �����߂邱�Ƃ͂ł��Ȃ��B�A�C�e�����P�̎��ɂ͂��̖��͂Ȃ��������A�A�C�e���@�@���Q�ȏ�ɂȂ�ƁA���̖��͕K����������B���̂��߁A�ʏ��Q�A�C�e���ȍ~�̑�P�J�e�S�����O�Ƃ��Čv�Z����B
�����@��i1���O�@�ii���Q�C3�@�c�j
�Ƃ��Ă�ij�����߂�B
��21���O �Ƃ����
![]() �@ �S��11�{�Q��22 ���Q�T
�@ �S��11�{�Q��22 ���Q�T
�@ �S��12�{�Q��22 ���P�T
�@ �Q��11�{�Q��12 ���Q�R�@
�@ �Q��11�{�Q��12�{�S��22 ���P�V
�����������
�@�@�@�@�@�@ ��11 = 7�@�@��12 = 4.5
��22 = �|1.5
����ė\������
�@�@�@�@�@�@�@�x = 7���11 �{ 4.5���12 �| 1.5���22 �Ƌ��߂���B
9.1.3�@�s����g�p���āA�\���������߂�B
�i�P�j���܁A�e�J�e�S���ɂ��čs����쐬���A�c�Ƃ����
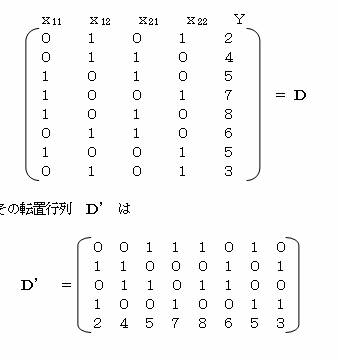
���ɁA�c�f�E�c�����߂�B
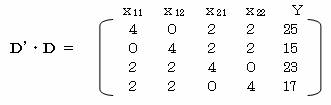
������݂�ƁA�e�s�����̂܂ܐ��K�������̌W���ɂȂ��Ă��邱�Ƃ�������B���ꂩ��
![]()
�S��11�{�Q��21�{�Q��22 ���Q�T
�@ �S��12�{�Q��21�{�Q��22 ���P�T
�@ �Q��11�{�Q��12�{�S��21 ���Q�R
�@ �Q��11�{�Q��12�{�S��22 ���P�V
�̕������āA��21���O�Ƃ��āA��ij�邱�Ƃ��ł���B
�i�Q�j�_�~�[�s����g�p���āA�\���������߂�B
�@�i�P�j�̕��@�ł́A�s�琳�K�������Ă�21���O�Ƃ��āA���������������̌W����ij�����߂����A�ŏ��ɍs��̂�21��������菜�����_�~�[�s����l���āA���ڂ�ij��
���߂�B
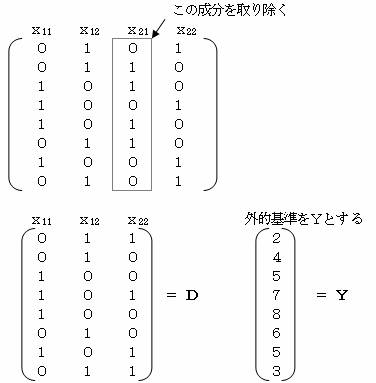
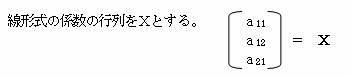
���̎��A�w
�́A �w���i�c�f��c�j-1��c�f��x �ŋ��߂邱�Ƃ��ł���B
��ʂ̏ꍇ�ł��A��Q�A�C�e���ȍ~�̑�P�J�e�S�����������s��A���`�\�����̌W�������߂邱�Ƃ��ł���B
�X�D�Q�@�J�e�S�����ʂ̊��
�ʏ���`�\���������߂�ɂ�����A��Q�A�C�e���ȍ~�̑�P�J�e�S���ɑΉ����鐔��
��i1 ���O�ii=2,3�c�j�Ƃ��ċ��߂Ă���̂ŁA��Q�A�C�e���ȍ~�̑�P�J�e�S�� �W���͏�ɂO�ƂȂ�B�����Ŋe�A�C�e�����̃J�e�S�����ʂ��O�ɂȂ�悤�ɃJ�e�S�����ʂ�ϊ�����B������J�e�S�����ʂ̊���Ƃ����B��������ƁA��Q�A�C�e���ȍ~�̑�P�J�e�S���̌W���𑼂̂��̂Ɠ����悤�ɓ��邱�Ƃ��ł���B
|
�W�{No |
�p�@�� |
���@�w |
�����l(��) �p��̓_�� |
�\���l(�x) �p��̓_�� |
||
|
�D�� |
���� |
�D�� |
���� |
|||
|
�P �Q �R �S �T �U �V �W |
�O �O �P �P �P �O �P �O |
�P �P �O �O �O �P �O �P |
�O �P �P �O �P �P �O �O |
�P �O �O �P �O �O �P �P |
�Q �S �T �V �W �U �T �R |
�R�D�O �S�D�T �V�D�O �T�D�T �V�D�O �S�D�T �T�D�T �R�D�O |
�\���l
�x �͗\�����@�x = 7���11 �{ 4.5���12 �| 1.5���22 ���狁�߂��l�B��̕\�ŁA�e�J�e�S���ɂ��Ă�ij���ij�����߂Ă�����
|
�W�{No |
�p�@�� |
���@�w |
�����l(��)�p��̓_�� |
�\���l(�x) �p��̓_�� |
||
|
��11 |
��12 |
��21 |
��22 |
|||
|
�P �Q �R �S �T �U �V �W |
0 0 7 7 7 0 7 0 |
4.5 4.5 0 0 0 4.5 0 4.5 |
0 0 0 0 0 0 0 0 |
�|1.5 0 0 �|1.5 0 0 �|1.5 �|1.5 |
2 4 5 7 8 6 5 3 |
3.0 4.5 7.0 5.5 7.0 4.5 5.5 3.0 |
|
���v |
28 |
18 |
0 |
�|6 |
40 |
40 |
|
���v |
46 |
�|6 |
40 |
40 |
||
|
���� |
5.75 |
�|0.75 |
5 |
5 |
||
��P�A�C�e�����̃J�e�S�����ρF5.75�A��Q�A�C�e�����̃J�e�S�����ρF�|0.75
�O�I��̕��ρF5 �ȏォ��A�e�A�C�e�����̕��ϒl���O����A ��������\���l
�x�f�́A�@
�x�f�| 5= (7�|5.75)���11 �{ (4.5�|5.75)���12 �| (0�{0.75)���21 �{ (�|1.5�{0.75)���22 �ƂȂ�B���ꂩ��
�x�f= 1.25���11 �| 1.25���12 �{ 0.75���21 �| 0.75���22 �{ 5 ����������Ƃ��̐��`�\�����ƂȂ�B ����������`�\���������߂�ɂ́A�e�W�����炻�̕��ς������ċ��߂��
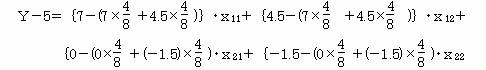
�x �� 1.25���11 �| 1.25���12 �{ 0.75���21 �| 0.75���22 �{ 5 ��������B
�X�D�R�@�d���W���ƕΑ��W��
�@�d��A���͂Ɠ��l�ɁA�����l���Ɛ��`�\�������狁�߂��\���l�x�Ƃ̑��W�����d���W���Ƃ����B�d���W�������Ƃ����
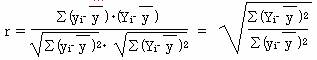
�d���W���̂Q��́A����W���i�q2 �j�ɓ������̂ŁA����W���ɂ�苁�߂����`�\�����̐��x�ׂ邱�Ƃ��ł���B�܂��A�e�A�C�e���̒P���W������d���W�������߂邱�Ƃ��ł���B
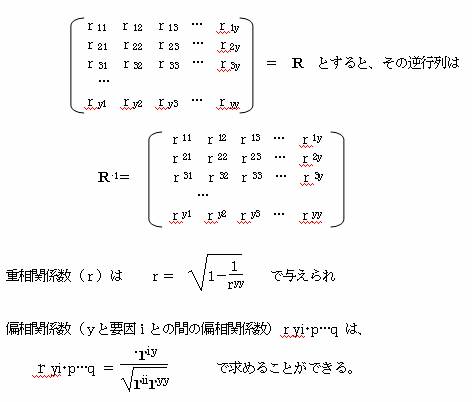
���܁A�A�C�e���P�C�Q�C�c�Ȃ�тɎ����l��������Ƃ��A���̒P���֍s���
|
�W�{No |
�A�C�e���P |
�A�C�e���Q |
�����l(��) �p��̓_�� |
||
|
��11 |
��12 |
��21 |
��22 |
||
|
�P �Q �R �S �T �U �V �W |
0 0 7 7 7 0 7 0 |
4.5 4.5 0 0 0 4.5 0 4.5 |
0 0 0 0 0 0 0 0 |
�|1.5 0 0 �|1.5 0 0 �|1.5 �|1.5 |
2 4 5 7 8 6 5 3 |
|
���� |
5.75 |
�|0.75 |
5 |
||
��̕\����A�A�C�e���P�E�A�C�e���Q�E�����l�i���j�Ԃ̒P���W���s������߂��

�ȏォ��A���̐��`�\�����ɂ��A�����l�̖�U�O������������Ă���A�A�C�e���P�Ǝ����l�Ƃ̕Α��W�����O�D�V�Q�X�A�A�C�e���Q�Ǝ����l�Ƃ̕Α��W�����O�D�T�R�X�ŃA�C�e���P�̕��������l�ɗ^����e���͑傫���̂ŁA���d�v�ȗv���ł���B
�X�D�S�@���`�\�����̕]���ɂ���
���߂����`�\�������A���Ƃ̃f�[�^���ǂꂭ�炢���m�ɗ\�����Ă���̂��A���̐��x��]������B
�@����W���i�q2�j���݂�B
�@����W���q2�́A�d���W���i���j�̂Q��Ɉ�v���Ă���A�O���q2���P�̒l�������B
�q2���P�ɋ߂��قǁA�����l��i�Ɨ\���l�xi�̑��ւ������A�悢�\���l�ł���Ƃ�����B
�A�͈́i�����W�j�ׂ�B
�@ �e�A�C�e�����̊e�J�e�S���ɗ^����������ꂽ���ʂ͈̔́i���ʂ̍ő�l�|���ʂ̍ŏ��l�j�������W�Ƃ����B�����W�̑傫���قNJO�I��ɗ^����e�����傫���̂ŁA���d�v�ȃJ�e�S���ł���B�A�C�e���P��1.25�|(�|1.25)=2.5 �A�C�e���Q��0.75�|(�|0.75)=1.5 �A�C�e���P�̕��������W�i�͈́j���傫���̂ŁA�A�C�e���P�̕����O�I��ɗ^����e���͑傫���B
�B�Α��W���ׂ�B
�e�A�C�e���ƊO�I��Ƃ̕Α��W����iy�ׁA��iy�̒l���傫���قNJO�I��ɗ^����e�����傫���̂ŁA���d�v�ȃA�C�e���ł���B
��y1.2��0.729
��y2.1��0.539 �ł��邩��A�A�C�e���P�̕����O�I��ɗ^����e���͑傫���B
���ʉ�1�ޗ��
�@�d��A���̗͂��́A�X���[���x�E����ʐρE���i�[���x�Ȃǂ��ʓI�f�[�^�ł������B��������܁A6�_�ȏ���u�ǂ��v�A5�_�ȉ����u�����v�Ǝ��I�f�[�^�ɂ��āA���ʉ�1�ނ̕��͂��s���B�d��A���̗͂������������Ɖ��̂悤�ȕ\�ƂȂ�B���̕\�����ɂ��ĕ��͂����{�B�Y������F�P�@�Y���Ȃ��F�O�@�Ƃ���B
|
�m�n |
�A�C�e��1 �X���[���x |
�A�C�e��2 �����ʐ� |
�A�C�e��3 ���i�[���x |
���㍂ �i�P�ʁF�S���~�j |
|||
|
�ǂ�a11 |
���� a12 |
�ǂ�a21 |
����a22 |
�ǂ� a31 |
���� a32 |
Y |
|
|
�P �Q �R �S �T �U �V �W |
�P �P �O �O �P �O �O �P |
�O �O �P �P �O �P �P �O |
�O �P �P �O �P �O �P �P |
�P �O �O �P �O �P �O �O |
�P �P �P �O �P �O �P �P |
�O �O �O �P �O �P �O �O |
�P�W �P�Q �P�S �U �P�Q �W �P�O �P�U |
�P�D�\���������߂�
1.1�@���K�������āA�\���������߂�B
�e�J�e�S���ɂ��čs���쐬���AD�Ƃ���B

D'�����߂�B
��TRANSPOSE(�͈́j�ɂ��AD�̓]�u�s��D'�����߂�B
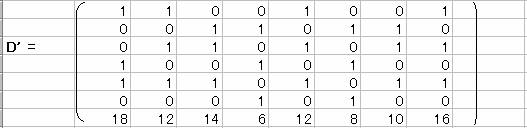
D'D�����߂�B
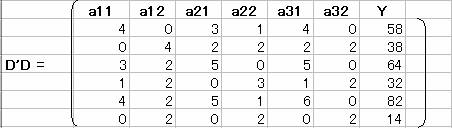
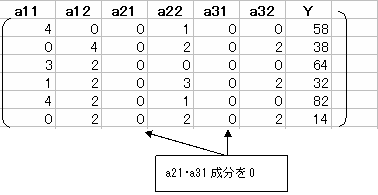 ����a21�Ea31���O�ɂ���B
����a21�Ea31���O�ɂ���B
�ȏォ�牺�̂悤�Ȑ��K��������B
![]() 4a11
+ a22 = 58
4a11
+ a22 = 58
4a12 + 2a22 + 2a32 =38
3a11 +2a12 =64
a11 + 2a12 + 3a22 + 2a32 =32
4a11 + 2a12 + a22 =82
2a12 + 2a22 + 2a32 = 14
����������ƁA
�@�@�@a11 = 13.33 a12 = 12 a21 = 0 a22 = 4.667 a31 = 0 a32 = �|9.667
1.2�@����a21�a31����菜�����s����g�p���ė\������B
����a21�a31����菜�����s���D�Ƃ����
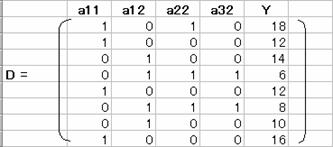
���̓]�u�s��D'�́A��TRANSPOSE(�͈́j�ɂ��AD�̓]�u�s��D'�����߂�B
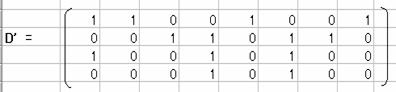
D'D�����߂�

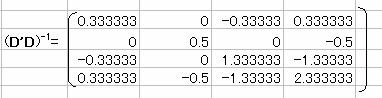
�iD'D)-1�����߂�
�iD'D)-1�D'�����߂�

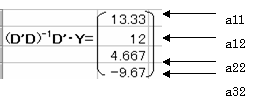 D'D)-1�D'�Y�����߂�
D'D)-1�D'�Y�����߂�
�ȏォ��
�@�@�@a11 = 13.33 a12 = 12 a21 = 0 a22 = 4.667 a31 = 0 a32 = �|9.667
�\�����́AY = 13.33X11 + 12X12 + 4.667X22 �| 9.667X32
1.3�@�\�����@Y = 13.33X11 + 12X12 + 4.667X22 �| 9.667X32�ŗ\���l�����߂�B
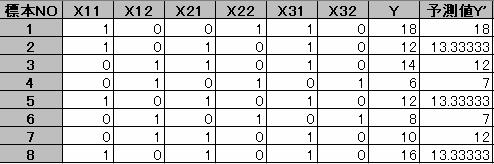
1.4�@�J�e�S�����ʂ̊�����s���B
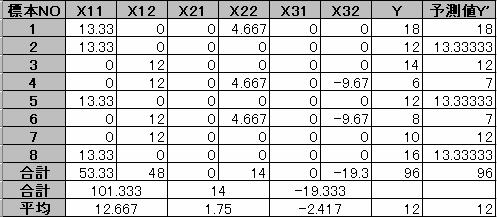
��1�A�C�e�����̃J�e�S�����ρF12.667�@��2�A�C�e�����̃J�e�S�����ρF1.75
��R�A�C�e�����̃J�e�S�����ρF�|2.417�@�O�I��̕��ρF12
�ȏォ��
��������\����Y'��
Y'�|12��(13.33�|12.667)X11+(12�|12.667)X12+(0�|1.75)X21+(4.667�|1.75)X22+(0�|(�|2.417))X31+(�| 9.667�|(�|2.417))X32
Y '= 0.667X11�|0.667X12�|1.75X21�{2.917X22�{2.41X31�|7.25X32�{12
���̊�������\�������g�p���ė\���l�����߂Ă������\���l�邱�Ƃ��ł���B
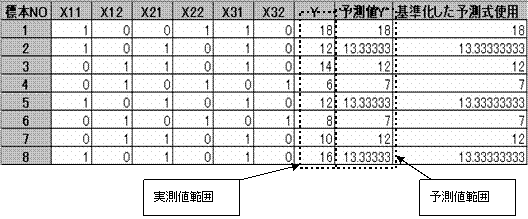
�Q�D�d���W���ƕΑ��W�������߂�B
2.1�@�����l�Ɨ\���l����d���W�����߂�B
�d���W���́A�����l�Ɨ\���l�̑��W���ł��邩��A��CORREL(�͈�1�C�͈�2)����d���W�������߂�B
�@�@�@�@R��CORREL(�����l�͈́A�\���l�͈́j��0.903037
2.2�@������ꂽ�J�e�S���f�[�^����d���W�������߂�B
aij�Xij�Ŋe�J�e�S�������߂�B
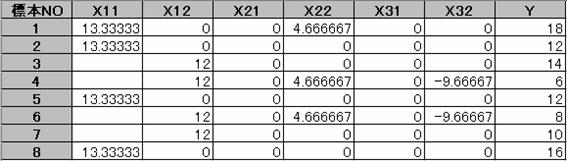
��̃f�[�^�ɂ����āA���ꂼ��̃A�C�e���̊e�J�e�S�������v����B
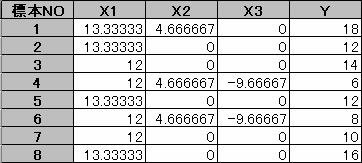
���̐V�����\��p���āA�����g�p���A�e�A�C�e���Ԃ̒P���W�������߂�B
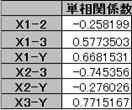
�P���W���s���R�Ƃ���
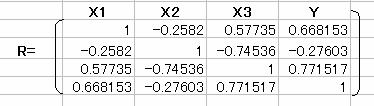
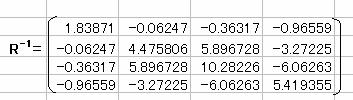 �P���W��R�̋t�s��R-1�����߂�B
�P���W��R�̋t�s��R-1�����߂�B

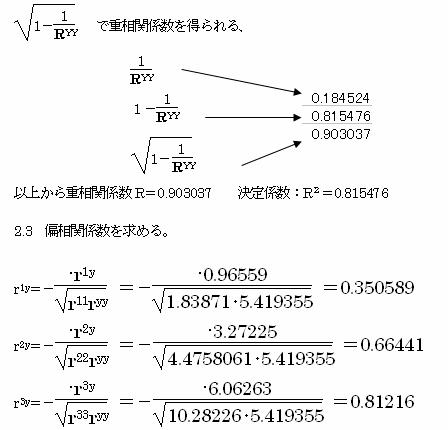
�ȏォ�狁�߂�ꂽ���`�\�����ɂ��A�����l�̖�81.5%����������Ă���A�A�C�e��3�̕Α��W������ԑ傫���̂ŁA�A�C�e��3�������Ƃ��d�v�ȗv���ł���Ƃ�����B
2.4�@�e�A�C�e���͈̔́i�����W�j�ׂ�B
�e�A�C�e���̃����W�͊�����ꂽ�J�e�S���f�[�^�̍ő�l�|�ŏ��l�ŋ��߂���B
![]() �@�@�@�A�C�e��1�F13.333�|12��1.333
�@�@�@�A�C�e��1�F13.333�|12��1.333
�@�@�@�A�C�e���Q�F4.667�|�O��4.667
�@�@�@�A�C�e���R�F0�|(�|9.667)��9.667
�A�C�e���R�̃����W����ԑ傫���A����ăA�C�e���R���O�I��ɗ^����e���������Ƃ��傫���̂ŁA�A�C�e���R����ԏd�v�ȗv���ł���B