10. 数量化Ⅱ類
説明変数が質的データで与えられ、この質的データから、質的データである外的基準を求める方法。説明変数が量的データで与えられているときには、判別分析があるが、説明変数が質的データで与えられるときに、いくつかの群に判別する方法が数量化Ⅱ類である。
6人の生徒について、英語と数学(アイテム)の好き・嫌い(カテゴリ)のアンケートをとり、そのアンケートの結果と入学試験に合格したか不合格であったかの結果が下の表のようになったとする。
|
標本No |
英語 |
数学 |
合否 |
||
|
好き |
嫌い |
好き |
嫌い |
||
|
1 2 3 4 5 6 |
レ レ レ レ |
レ レ |
レ レ |
レ レ レ レ |
合 合 合 否 否 否 |
10.1 判別式を求める。
数量化Ⅰ類同様に、各アイテムの各カテゴリについて、該当有りは1、該当無しは0の 数量を与える。
![]() ダミー変数として
ダミー変数として
1…該当有り
xi(jk) =
0…該当なし
|
標本No |
アイテム1 英語 |
アイテム2 数学 |
合否 (外的基準) |
||
|
x11 |
x12 |
x21 |
x22 |
||
|
1 2 3 4 5 6 |
1 1 1 0 0 1 |
0 0 0 1 1 0 |
1 1 0 0 0 0 |
0 0 1 1 1 1 |
合 合 合 否 否 否 |
説明変数は、数量化により質的データに量的データを与える。結果の合否は、質的データ(区分データ)である。量的データと質的データの関係を表すものとして相関比(η)がある。相関比(η)は、級間変動÷全変動で与えられる。
いま、各カテゴリをx11・x12・x21・x22とし、これらのカテゴリから求められる合成変量(以下判別得点と呼ぶことにする)をYとすると、Y=a11・x11+a12・x12+a21・x21+a22・x22
この式を使用して、実際に各標本の判別得点を求めると次のような表になる。
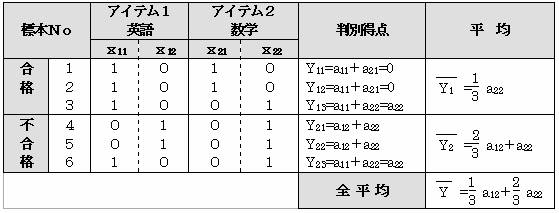
数量化Ⅰ類と同様にダミー変数間に、xi(11)+xi(21)=xi(21)+xi(22)=1の関係があるので、このままではaij を求めることができない。このために数量化Ⅱ類では、通常ai1=0とする。(a11=a21=0)
判別得点から相関比を求め、相関比が最大になるようなaij を求める。相関比が最大になれば、2群が最もよく区分されているといえる。相関比(η)は、全変動をST、級間変動をSB とすると η2 =ST÷SB で与えられる。
①全変動を求める。
全変動は、各データが全平均からどれくらいバラついているかである。
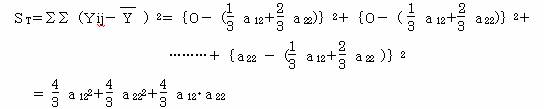
②級間変動を求める。
級間変動は、1群の平均が全平均からどれくらいバラついているかと、2群の平均が全平均からどれくらいバラついているかの合計である。
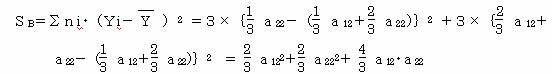
③相関比を求める。

相関比をtで偏微分し、0とおいて相関比を最大にするtを求める。

この判別式から判別得点を求めると、下の表のようになる。
|
群 |
標本No |
アイテム1 |
アイテム2 |
判別得点 Y |
平 均 |
||
|
英語 |
数学 |
||||||
|
x11 |
x12 |
x21 |
x22 |
||||
|
合 格 |
1 2 3 |
1 1 1 |
0 0 0 |
1 1 0 |
0 0 1 |
0 0 0.707 |
0.2356 |
|
不 合 格 |
4 5 6 |
0 0 1 |
1 1 0 |
0 0 0 |
1 1 1 |
1.414 1.414 0.707 |
1.178 |
|
|
全 平 均 |
0.707 |
|||||
この時相関比は
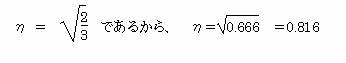
10.2 行列を使用して判別式を求める。
相関比をηとすると
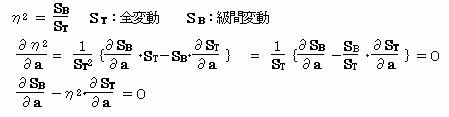
例題のような2群の判別の時を考える
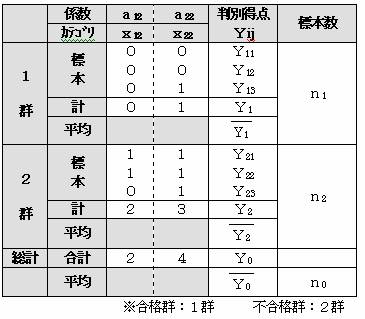
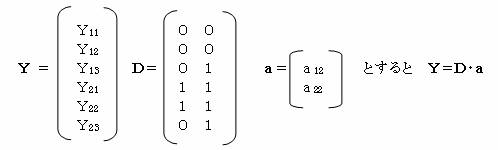
1群の計を(0,1)=c、2群の計を(2,3)=d、総計を(2,4)=bとすると
1群の判別得点の合計は、Y1=c・a 2群の判別得点の合計は、Y2=d・a
判別得点の総計は、Y0=b・a
全分散ST、級間分散をSBは

行列T、Bはともに対称行列
![]()
|2B・a-2η2・T・a|=0 2|B-η2・T|・a=0 |B-η2・T|=0
|T-1・B-η2・E|=0 これより、相関比を得る。
例題について、説明変数を行列で表すと
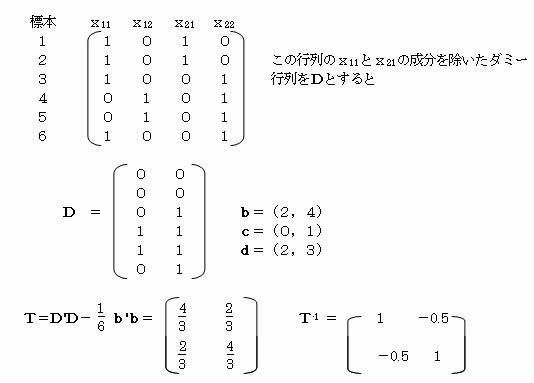

![]() 0.333a12+0.333a22=0.666a12
0.333a12+0.333a22=0.666a12
0.333a12+0.333a22=0.666a22
a122+a222 = 1
![]()
10.3 カテゴリ数量の基準化
数量化Ⅱ類では、判別式を得るにあたり、第1カテゴリに対応する数量をai1=0(i=1,2…)として求めているので、この結果a11=0、a21=0
となるので、各アイテム内のカテゴリ数量の平均が0になるように基準化を行う。
最初に求めた判別式は、Y=0.707・x12+0.707・x22 であるから、これを基準化する。
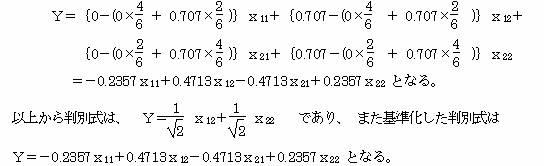
この基準化した判別式を用いて、それぞれの標本の判別得点を求めて表にすると
|
群 |
標本No |
アイテム1(英語) |
アイテム2(数学) |
判別得点 Y |
平均 |
||
|
x11 |
x12 |
x21 |
x22 |
||||
|
合 格 |
1 2 3 |
-0.2357 -0.2357 -0.2357 |
0 0 0 |
-0.4713 -0.4713 0 |
0 0 0.2357 |
-0.707 -0.707 0 |
-0.471 |
|
不 合 格 |
4 5 6 |
0 0 -0.2357 |
0.4713 0.4713 0 |
0 0 0 |
0.2357 0.2357 0.2357 |
0.707 0.707 0 |
0.471 |
|
|
合計 |
-0.943 |
0.943 |
-0.943 |
0.943 |
|
|
|
合計 |
0 |
0 |
|||||
|
平均 |
0 |
0 |
|||||
10.4 外的基準に与えるアイテムの影響力について
どのアイテムが一番外的基準に影響を与えているかを調べるには、レンジ(範囲)・単相関係数・偏相関係数をみるようにする。外的基準に与える影響力の大きいアイテムほど重要なアイテムであるといえる。
(1)レンジ(範囲)を調べる。
数量化Ⅰ類と同様に、各アイテム内の基準化されたカテゴリ数量の「最大値-最小値」をレンジ(範囲)という。レンジの大きいアイテムほど外的基準に与える影響が大きいといえる。
|
標本No |
アイテム1(英語) |
アイテム2(数学) |
|
1 2 3 |
-0.2357 -0.2357 -0.2357 |
-0.4713 -0.4713 0.2357 |
|
4 5 6 |
0.4713 0.4713 -0.2357 |
0.2357 0.2357 0.2357 |
|
レンジ |
0.707 |
0.707 |
レンジを求めると
アイテム1… 0.4713-(-0.2357)=0.707
アイテム2… 0.2357-(-0.4713)=0.707
アイテム1・アイテム2ともにレンジは 0.707 であり、アイテム1・アイテム2ともにレンジからみると外的基準に与える影響力差はないといえる。
(2)各アイテムと外的基準との間の単相関係数を調べる。
外的基準は、「合格」「不合格」といった質的データであるから、この外的基準に対して数量を与える。外的基準が2群であれば、よく2群を区別できるように「合格」に対して「-1」を与え、また「不合格」に対して「1」を与えると次のような表となる。
|
標本No |
アイテム1(英語) x1 |
アイテム2(数学) x2 |
外的基準 y |
|
1 2 3 4 5 6 |
-0.2357 -0.2357 -0.2357 0.4713 0.4713 -0.2357 |
-0.4713 -0.4713 0.2357 0.2357 0.2357 0.2357 |
-1(合格) -1(合格) -1(合格) 1(不合) 1(不合) 1(不合) |
アイテム1をx1、アイテム2をx2、外的基準をy、またアイテム1と外的基準との単相関係数をr1y、アイテム2と外的基準との単相関係数をr2yとすると、それぞれの単相関係数は
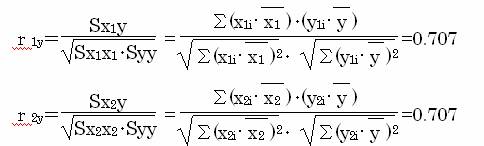
それぞれの説明変量と外的基準との単相関係数についても、アイテム1とアイテム2は同じであり、同等の影響を与えている。
なお、説明変量間でお互いに高い相関が認められるときには、多重共線性を示すので、その時にはどちらか一方の説明変量を落として判別式を求めるようにする必要がある。
いまアイテム1とアイテム2の間の相関係数を求めると、r12=0.5であり、それほど高い相関はないと認められるので、多重共線性はないといえる。
(3)各アイテムと外的基準との偏相関係数を調べる。
数量化Ⅰ類と同様にして、各説明変量と外的基準との偏相関係数を求める。

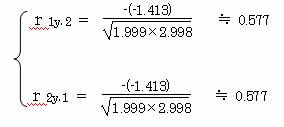
偏相関係数についても、外的基準に与える2つのアイテムの影響力は同じであるといえる。
数量化2類例題
判別分析の例題は、説明変量が量的データであり、目的変量が質的データであった。この表を元にして、説明変量において、6点以上を該当あり、5点以下を該当無しとして新しい表を作成する。この新しく作成された表はすべて質的データであるから、数量化2類の分析を実施する。
判別分析で使用した表
|
NO |
X1 礼儀 |
X2 積極性 |
X3 強調性 |
X4 業界区分 |
|
1 2 3 4 5 6 7 8 |
3 8 6 8 7 4 6 7 |
8 2 7 6 3 7 3 5 |
4 6 6 4 5 3 6 8 |
A B A A B A B B |
1. 数量化2類分析用に質的データの表にする。
6点以上を該当有り:「1」 5点以下を該当無し:「0」 A業界:「1」 B業界:「2」とする。
|
NO |
X1 礼儀 |
X2 積極性 |
X3 強調性 |
Y 業界区分 |
|||
|
|
有り |
無し |
有り |
無し |
有り |
無し |
|
|
1 2 3 4 5 6 7 8 |
0 1 1 1 1 0 1 1 |
1 0 0 0 0 1 0 0 |
1 0 1 1 0 1 0 0 |
0 1 0 0 1 0 1 1 |
0 1 1 0 0 0 1 1 |
1 0 0 1 1 1 0 0 |
1 2 1 1 2 1 2 2 |
新しく作成した表を見ると、説明変量X2と目的変量Yが1対1で対応状態となっている。このままでは変量X2さえあれば、他の変量はいらないということになるので、X2の変量を削除する。説明変量X1・X3と目的変量Yの表
|
|
礼儀: |
X1 |
協調性: |
X3 |
業界区分 |
|
|
有り |
無し |
有り |
無し |
|
|
標本 |
X11 |
X12 |
X31 |
X32 |
Y |
|
1 |
0 |
1 |
0 |
1 |
1 |
|
2 |
1 |
0 |
1 |
0 |
2 |
|
3 |
1 |
0 |
1 |
0 |
1 |
|
4 |
1 |
0 |
0 |
1 |
1 |
|
5 |
1 |
0 |
0 |
1 |
2 |
|
6 |
0 |
1 |
0 |
1 |
1 |
|
7 |
1 |
0 |
1 |
0 |
2 |
|
8 |
1 |
0 |
1 |
0 |
2 |
上の表のデータを元にして数量化2類の分析を実施する。
X11・X31の成分を取り除き、業界区分をキーとして昇順にソートし、2群に分ける。
さらに各群の小計と2群の合計を求めると以下の様な表になる。
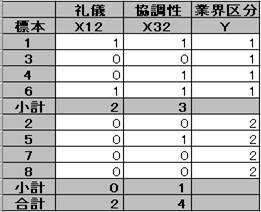
2. 上の表を元に線形判別式を求める。
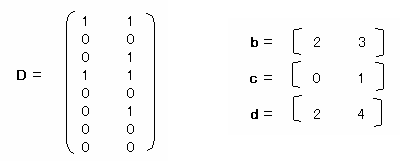
とすると

(0.25-η2 )・(0.125-η2)-0.25×0.125=0
η2= 0,0.375
分散比(η2)は0で最小となり、0.375で最大となる。

![]() 0.25a12+025 a32=0.375a12
0.25a12+025 a32=0.375a12
0.125 a12+0.125 a32=0.375a32
a122+a322=1
以上から a12 = 0.894 a32 = 0.447
線形判別式は、Y= 0.894X12 + 0.447X32
この式を基準化すると、Y= -0.2235X11+0.6705X12-0.2235X31+0.2235X32
この判別式を使用して予測値(Y')を求める。さらに求めた予測値の標準偏差を求め、各予測値を割って標準化(平均:0 標準偏差:1)する。さらに標準化された予測値の各群の平均値を求める。
|
|
礼儀 |
|
協調性 |
|
業界区分 |
|
|
|
|
|
有り |
無し |
有り |
無し |
|
予測値 |
標準化 |
|
|
標本 |
X11 |
X12 |
X31 |
X32 |
Y |
Y' |
Y' |
各群平均 |
|
1 |
0 |
1 |
0 |
1 |
1 |
0.894 |
1.52753 |
|
|
3 |
1 |
0 |
1 |
0 |
1 |
-0.447 |
-0.7638 |
|
|
4 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
|
6 |
0 |
1 |
0 |
1 |
1 |
0.894 |
1.52753 |
0.5728 |
|
2 |
1 |
0 |
1 |
0 |
2 |
-0.447 |
-0.7638 |
|
|
5 |
1 |
0 |
0 |
1 |
2 |
0 |
0 |
|
|
7 |
1 |
0 |
1 |
0 |
2 |
-0.447 |
-0.7638 |
|
|
8 |
1 |
0 |
1 |
0 |
2 |
-0.447 |
-0.7638 |
-0.573 |
|
|
|
|
|
|
平均 |
0 |
0 |
|
|
|
|
|
|
|
標準偏差 |
0.58526 |
1 |
|
以上から1群(A社)の重心:0.573 2群(B社)の重心:-0.573 である。
3.レンジ(範囲)を調べる。
各アイテムの各カテゴリを基準化して、最大値-最小値からレンジを求める。
|
|
礼儀 |
|
協調性 |
|
業界区分 |
|
|
有り |
無し |
有り |
無し |
|
|
標本 |
X11 |
X12 |
X31 |
X32 |
Y |
|
1 |
0 |
0.6705 |
0 |
0.2235 |
1 |
|
3 |
-0.2235 |
0 |
-0.2235 |
0 |
1 |
|
4 |
-0.2235 |
0 |
0 |
0.2235 |
1 |
|
6 |
0 |
0.6705 |
0 |
0.2235 |
1 |
|
2 |
-0.2235 |
0 |
-0.2235 |
0 |
2 |
|
5 |
-0.2235 |
0 |
0 |
0.2235 |
2 |
|
7 |
-0.2235 |
0 |
-0.2235 |
0 |
2 |
|
8 |
-0.2235 |
0 |
-0.2235 |
0 |
2 |
|
合計 |
-1.341 |
1.341 |
-0.894 |
0.894 |
|
![]() アイテム1:0.6705-(-0.2235)=0.894
アイテム1:0.6705-(-0.2235)=0.894
アイテム2:0.2235-(-0.2235)=0.447
アイテム1(礼儀)の方がレンジが大きい。よってアイテム1の方が外的基準に与える影響は大きい。
4.各アイテムと外的基準間の単相関係数を調べる。
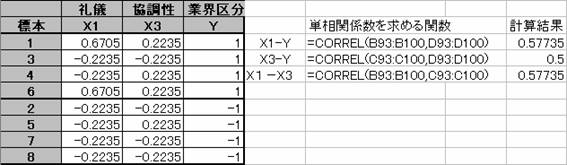
B業界区分に数量-1を与える。
X1(礼儀)とYの単相関係数:0.57735 X2とYの単相関係数:0.5
X1の単相関係数が大きい。X1(礼儀)の方が外的基準に与える影響は大きい。
またX1-X3の単相関係数:0.57735であり、X1-X3間の多重共線性はないと考えられる。
5.偏相関係数を調べる。
相関係数行列を作成し、その逆行列を求める。
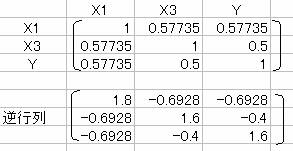
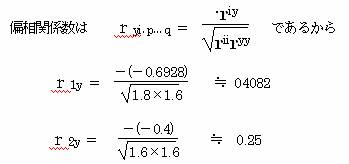
各アイテムと外的基準との偏相関係数も、X1-Yの方が大きい。X1(礼儀)の外的基準に与える影響の方が大きい。