11. 数量化Ⅲ類
数量化Ⅰ類およびⅡ類では求めるべき外的基準があったが、数量化Ⅲ類では求めるべき外的基準がなく、与えられた質的データについて、そのデータの類似性について調べる方法である。項目(カテゴリ)と被験者(サンプル)について、両方同時に数量化を行い、項目と被験者の相互の関連をより明らかにする方法である。パターン類似法とも呼ばれている。量的データの分析である主成分分析に似た質的データの分析方法である。
項目(カテゴリ)と被験者(サンプル)について、質的データが与えられているとき、同一の項目に反応した被験者は類似性が高く、また同一の被験者に反応した項目は類似性が高いと仮定する。お互いに類似性の高い項目・被験者が近くにくるように並べかえると反応したものが対角線の周辺に集まってくる。このようにして、その類似性を調べようとするのであるが、項目と被験者を並べかえる代わりに、項目と被験者の相関係数を最大にすることにより実施する。
いま、4人の被験者について、野球とすもうのどのスポーツが好きかを調べたところ、下のような表な結果を得た。この結果から被験者の類似性や項目間の類似性を調べる。
好きなスポーツ項目に「レ」をつける。
|
|
カテゴリ(項目) |
|||
|
被 験 者 |
サ ン プ ル |
No |
野球 |
すもう |
|
1 2 3 4 |
レ レ レ |
レ レ |
||
上の表について、「該当有り」には「1」を、「該当無し」には「0」の数量を与えると
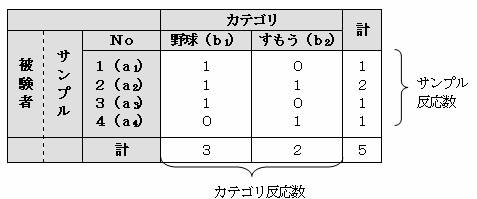
11.1 サンプルスコア・カテゴリスコアを求める。
サンプルデータの分散をVaa、カテゴリデータの分散をVbb、サンプルデータとカテゴリデータの共分散をVabとすると
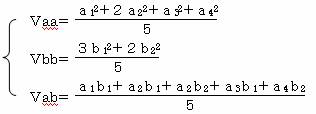

![]()
この式をa1・a2・a3・a4 とb1・b2 で偏微分し0とおくことにより、相関係数Rを最大にするai・bjを求める。
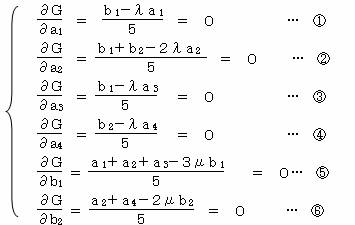
①×a1+②×a2+③×a3+④×a4を求めると
a1b1+a2b1+a2b2+a3b1+a4b2-λ(a12+2a22+a32+a42)
=
a1b1+a2b1+a2b2+a3b1+a4b2-λ
⑤×b1+⑥×b2を求めると
a1b1+a2b1+a2b2+a3b1+a4b2-μ(3b12+2b22)
=
a1b1+a2b1+a2b2+a3b1+a4b2-μ
これから λ=μ
①②③④から
![]()
これを⑤⑥に代入して
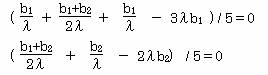
よって 5b1+b2-6λ2b1=0
… ⑦
b1+3b2-4λ2b2=0
… ⑧
⑦⑧を変形して
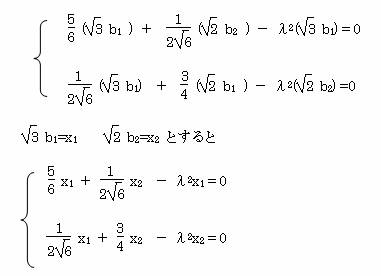
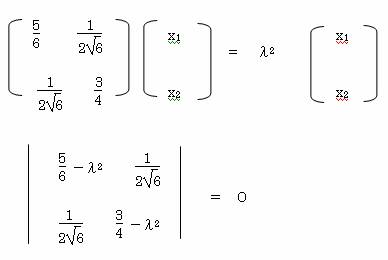
この式から
λ2 =1 ,0.583
数量化Ⅲ類では、得られた固有方程式を解くと、固有値の1つとして必ず1が得られるが、この解の1は採用しないで(全部同じ値となり意味がない)、2番目以降の固有値から採用する ようにする。λ2=0.583を採用し、固有ベクトルb1・b2 を求める。

以上をまとめると
[カテゴリスコア]
|
カテゴリ |
カテゴリスコア |
|
野球(b1) すもう(b2) |
0.365 -0.548 |
[サンプルスコア]
|
サンプル |
サンプルスコア |
|
1(a1) 2(a2) 3(a3) 4(a4) |
0.478 -0.120 0.478 -0.718 |
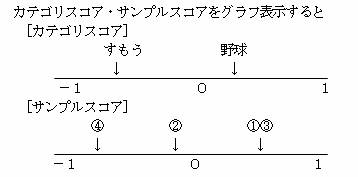
カテゴリ数・サンプル数が少ないためにそれぞれの類似性がはっきりしないが、サンプルス コアを見ると、①と③の被験者の嗜好が同じであり、②と④の被験者の嗜好が近いといえる。 一般にカテゴリ数がn個あると、固有値もn個求められるが、数量化Ⅲ類では、固有値の中で最大の固有値は、常に1となるのでこれを除いたn-1個の固有値を採用する。
11.2 行列を使用して、サンプルスコア・カテゴリスコアを求める。
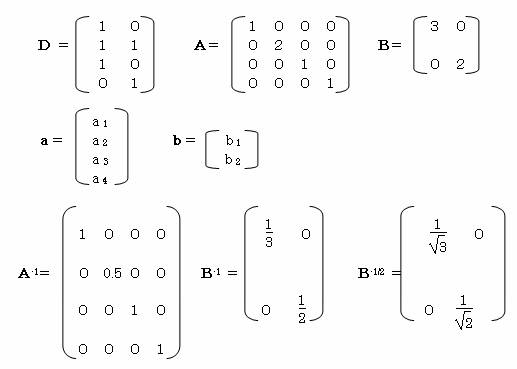
カテゴリ数やサンプル数が増えてくると計算が非常に大変になる。そこで、同様の計算を行 列を用いて実施する。各行列を下のようにする。
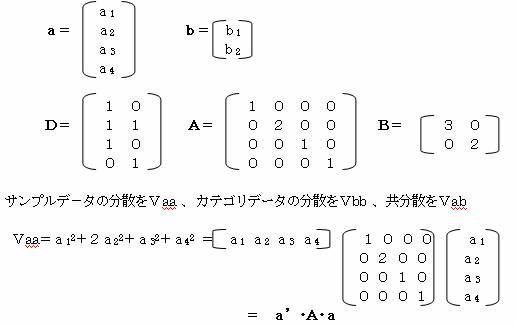

これを変形すると
B-1/2・D’・A-1・D・B-1/2・x-λ2・x=0
ただし B1/2・b=xとする
(B-1/2・D’・A-1・D・B-1/2-λ2)x=0
|B-1/2・ D’・A-1・D・B-1/2
-λ2E|=0 よりλ2を得る。
実際に行列を使用して、カテゴリスコア・サンプルスコアを求める。
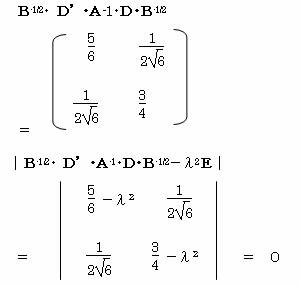
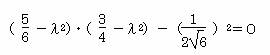
λ2 =1
,0.583
固有値λ2=1を除いて、λ2=0.583を採用する。
λ2=0.583に属する固有ベクトルbを求める。
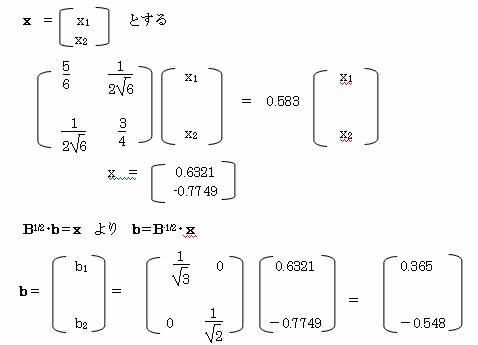
これより、b1=0.365 b2=-0.548
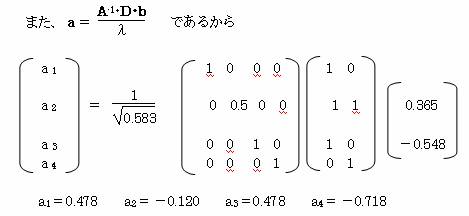
11.3 アイテム・カテゴリ方式
いままで行ってきた数量化Ⅲ類の方法は、1つの項目について「好き」「嫌い」のように2者択一的に選択するという方法をとったが、1つの項目について「好き」「普通」「嫌い」のように選択支が2つ以上ある時には、このような方法は使用できない。選択支がつ以上ある時には、アイテム・カテゴリ方式で求める必要がある。
前の表をアイテム・カテゴリ方式で新しく表を作成すると、下のようになる。
|
N0 |
野 球 |
すもう |
||
|
好き(b1) |
嫌い(b2) |
好き(b3) |
嫌い(b4) |
|
|
1 2 3 4 |
○ ○ ○ × |
× × × ○ |
× ○ × ○ |
○ × ○ × |
該当するカテゴリは1、該当しないときは0の数量を与える。
該当するカテゴリは1、該当しない時には0の数量を与える。
|
N0 |
野 球 |
すもう |
計 |
||
|
好き(b1) |
嫌い(b2) |
好き(b3) |
嫌い(b4) |
||
|
1(a1) 2(a2) 3(a3) 4(a4) |
1 1 1 0 |
0 0 0 1 |
0 1 0 1 |
1 0 1 0 |
2 2 2 2 |
|
計 |
3 |
1 |
2 |
2 |
8 |
①サンプルスコア・カテゴリスコアを求める。
前回の方法と同様にして計算し、それぞれの得点を求める。
サンプルデ-タの分散Vaa、カテゴリデータの分散Vbb、共分散Vabを求めると
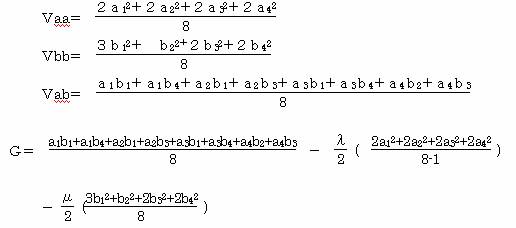

前回と同様にλ=μとなるので
①②③④から
a1= a2= a3= a4=
これを、それぞれ⑤⑥⑦⑧に代入すると
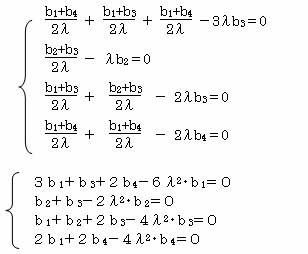
この式から固有値を求めると、λ2=1 , 0 , 0.789 , 0.211
λ2=1 , 0 は無意味なので λ2=0.789 , 0.211 を採用する。
λ2= 0.789 , 0.211 を採用し、それぞれに属する固有ベクトルを求める。
①λ2=0.789 の時
3b1+b3+2b4-6×0.789・b1=0
b2+b3-2×0.789・b2=0
b1+b2+2b3-4×0.789・b3=0
2b1+2b4-4×0.789・b4=0
以上から、b1=-0.57・b3 b2=1.73・b3 b4=-b3
b3=1 とすると、b1=-0.57 b2=1.73 b4=-1
また標準化すると
b1=-0.188 b2=0.577 b3=0.33 b4=-0.33
サンプルスコアを求めると
![]()
a1=-0.88 a2=0.24 a3=-0.88 a4=1.53
②同様にして、λ2 =0.211 の時のカテゴリスコア・サンプルスコアを求めると
b1=0.577 b2=-1.73 b3=1
b4=-1
a1=-0.46
a2=1.72 a3=-0.46
a4=-0.79
[カテゴリスコア]
|
λ2 |
野 球 |
すもう |
||
|
好(b1) |
嫌(b2) |
好(b3) |
嫌(b4) |
|
|
0.789 0.211 |
-0.57 0.57 |
1.73 -1.73 |
1 1 |
-1 -1 |
λ12= 0.789 を横軸に,λ22= 0.211 を縦軸にとりカテゴリスコアをグラフに描くと
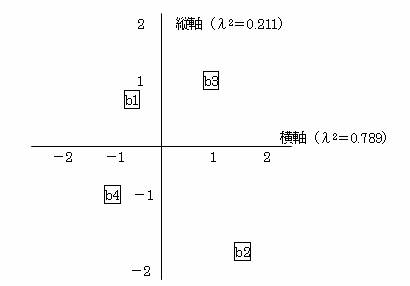
グラフを見ると横軸の+方向は、個人戦のスポーツが好き、-方向は団体戦のスポーツが好きな傾向と考えられる。また縦軸の+方向は全般的にスポーツが好きな傾向、-方向は全般的にスポーツが嫌いな傾向を示すと考えられる。
[サンプルスコア]
|
被験者 |
固有値 |
|
|
λ12:0.211 |
λ22:0.789 |
|
|
a1 a2 a3 a4 |
-0.88 0.24 -0.88 1.53 |
-0.46 1.72 -0.46 -0.79 |
サンプルスコアをみると、被験者の嗜好の類似性を見ることができる。
λ12= 0.789 を横軸に,λ22= 0.211 を縦軸にとりサンプルスコアをグラフに描くと
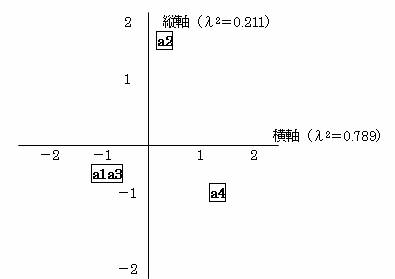
数量化3類例題
主成分分析の例題を使用し、数量化3類の分析を実施する。ビジネスのカテゴリを削除し、それぞれのカテゴリで、該当あり:1 該当なし:0 の数量を与える。またカテゴリ反応数、アイテム反応数を求めておく。
|
|
ニュース |
スポーツ |
|
||
|
|
充実 |
不充実 |
充実 |
不充実 |
カテゴリ |
|
NO |
X11 |
X12 |
X31 |
X32 |
反応数 |
|
1 |
1 |
0 |
0 |
1 |
2 |
|
2 |
0 |
1 |
1 |
0 |
2 |
|
3 |
1 |
0 |
1 |
0 |
2 |
|
4 |
0 |
1 |
0 |
1 |
2 |
|
5 |
1 |
0 |
1 |
0 |
2 |
|
6 |
0 |
1 |
0 |
1 |
2 |
|
7 |
0 |
1 |
1 |
0 |
2 |
|
8 |
1 |
0 |
0 |
1 |
2 |
|
9 |
0 |
1 |
0 |
1 |
2 |
|
10 |
1 |
0 |
1 |
0 |
2 |
|
サンプル反応数 |
5 |
5 |
5 |
5 |
|
1. カテゴリスコア・サンプルスコアを求める。

とする。
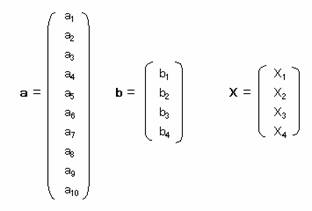 また
また
とする。aはサンプルスコア、bはカテゴリスコア、Xは固有ベクトルを求めるため行列である。
![]()
![]() 以上から B-1/2・D'・A-1・D・B-1/2 を求める。
以上から B-1/2・D'・A-1・D・B-1/2 を求める。
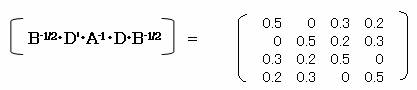

1.1.1 カテゴリスコアを求める。
b = B-1/2・Xより

求められたカテゴリスコアを更にその標準偏差で割って基準化すると
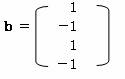
1.1.2 サンプルスコアを求める。
a = A-1・D・bより
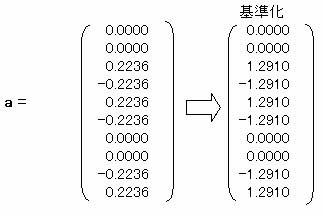
1.2 λ2=0.4 の時
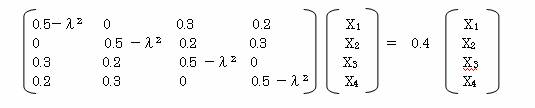
X1=0.5 X2=-0.5 X3=-0.5 X4=0.5
1.2.1 カテゴリスコアを求める。
b = B-1/2・Xより

求められたカテゴリスコアを更にその標準偏差で割って基準化すると
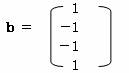
1.2.2 サンプルスコアを求める。
a = A-1・D・bより
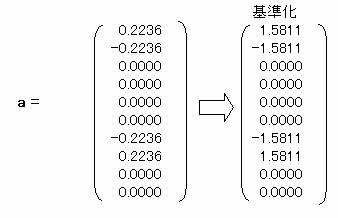
以上をまとめると
カテゴリスコア
|
λ2 |
ニュース |
スポーツ |
||
|
充実 |
不充実 |
充実 |
不充実 |
|
|
b11 |
b12 |
b31 |
b32 |
|
|
0.6 |
0.5 |
-0.5 |
0.5 |
-0.5 |
|
0.4 |
0.5 |
-0.5 |
-0.5 |
0.5 |
カテゴリスコアをグラフ化する
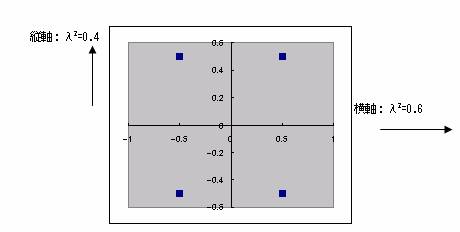
λ2=0.6を横軸に、λ2=0.4を縦軸にとりカテゴリスコアをグラフ化する。
これを見ると、横軸の+方向に紙面の充実度の程度、縦軸+方向に専門紙指向、-方向に大衆紙指向の度合いと考えられる。
次にサンプルスコアを同様にグラフ化する。
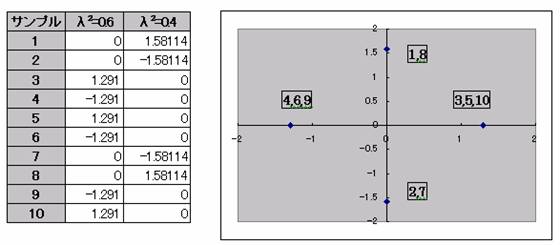
λ2=0.6を横軸に、λ2=0.4を縦軸にとりサンプルをグラフ化する。
横軸の+方向に紙面の充実度の程度、縦軸+方向に専門紙指向、-方向に大衆紙指向の度合いと考えられるので、紙面の充実度の高いのは、3,5,10の3紙であり、不充実の紙は4,6,9の3紙である。専門紙志向が強いのは、1,8の2紙であり、大衆紙志向の強いのは、2,7の2紙である。