EXCEL多変量分析ホームページへ戻る

１．回帰分析

　何名かの体重と身長の値が分かっているとき、体重の値は分かっているが、身長が不明の人がいるとする。このようなとき、すでに得ているデータから身長と体重の関係を調べ、その相関を求め、身長不明の人の身長を予測する。この様な分析方法を回帰分析という。

求めるものは身長であり、これを目的変量と呼ぶ。身長の値を予測するのは、体重からであるので、この体重のことを説明変量と呼ぶ。説明変量が１つの時を単回帰分析といい、説明変量が２つ以上の時を多重回帰分析という。

回帰分析では、説明変量は量的データであり、また目的変量も量的データである。

なお、回帰式で予測をするときには、説明変量の範囲内で予測することが望ましい。説明変量の範囲を大きく越えたところで予測すると誤差が大きくなり実用に適さなくなる。

１．１　単回帰分析

　正規母集団から抽出して得られた標本データｘ・ｙが下表のようにあり、ｘ・ｙ間にある関係があるものとする。

標　本	説明変量ｘ	目的変量ｙ
１ ２ … ｎ	ｘ1 ｘ2 … ｘn	ｙ1 ｙ2 … ｙn

以上の標本データをＸＹグラフで描くいて、下のようになったとする

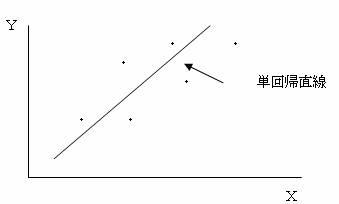
標本データｘ・ｙの間には右上がりの関係がありそうなので、ｘとｙの関係を表す適当な直線を考える。 目的変量ｙと説明変量ｘとの間に相関があるとき、

　Ｙ＝ｂ₁･ｘ＋ｂ₀　なる直線を１本考え、実データとこの直線上の値との差をεとする。

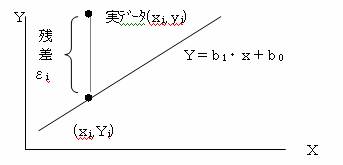
Ｙ＝ｂ₁･ｘ＋ｂ₀　なる直線は全ての標本データについて、

その残差が最小になるようにひく必要がある。この直線から各標本データとのズレ具合いを計るために、各残差の平方和をとり、この平方和を最小にするようにする。このような方法を最小２乗法という。

　標本データは、直線Ｙ＝ｂ₁･ｘ＋ｂ₀ から残差（ε）分ずれているので、標本データは

ｙ＝ｂ₁･ｘ＋ｂ₀ ＋εと表す。

　このことから線形回帰モデルを

　ｙ_i＝β₁･ｘ_i＋β₀＋ε_i　（i＝1,2…ｎ）とすると

残差εについて、

　　�@ε_iとε_jはお互いに独立であり、正規分布　Ｎ（０，σ²）に従う。

　　�Aε_iの平均値（期待値）は０である。

　　�Bε_iの分散は一定である。　

このような仮定下で単回帰式を Ｙ＝ｂ₁･ｘ＋ｂ₀ とする。

いま、残差εに注目すると　ε_i＝ｙ_i−Ｙ_i　ε_i＝ｙ_i−ｂ₁･ｘ_i−ｂ₀　である。

この残差を全ての標本データについて合計し、その合計値を最小にするようなｂ₀・ｂ₁ を求め、この単回帰式を得る。

�買ﾃ_i² ＝�煤iｙ_i−ｂ₁･ｘ_i−ｂ₀）² であるから

　ｆ＝�煤iｙ_i−ｂ₁･ｘ_i−ｂ₀）²とすると

この式をｂ⁰，ｂ₁で偏微分して、０とおくことにより、正規方程式を得て、式ｆを最小 にするｂ₀・ｂ₁を得ることができる。

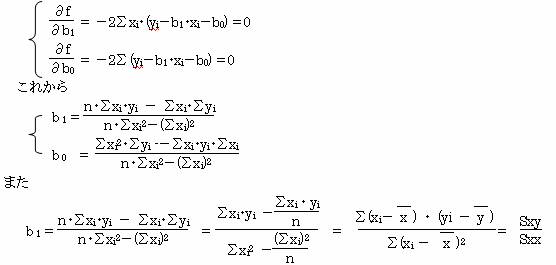
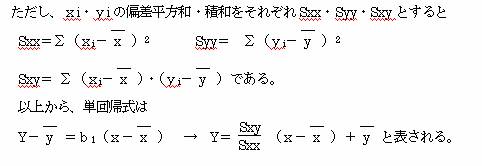
またｘとｙの相関係数をR_xyとすると

１．２　重回帰分析

それでは次に説明変量がｘ₁･ｘ₂の２変量になったときの回帰式を求める。

標　本	説明変量ｘ1	説明変量ｘ2	目的変量ｙ
１ ２ … ｎ	ｘ11 ｘ12 … ｘ1n	ｘ21 ｘ22 … ｘ2n	ｙ1 ｙ2 … ｙn

説明変量が２変量あるので、単純に説明２変量（ｘ₁とｘ₂）の平均値をとって、その値と目的変量（ｙ）との相関を求めても、平均値をとる段階で失う情報量が大きいので正しい回帰式を得ることができない。

このように説明変量が２つ以上ある時の回帰分析を重回帰分析という。

1.2.1　重回帰式を求める。

　２説明変量が次のようになっているときの重回帰直線を求める。

この関係を図で表すと

　　　　　　　　

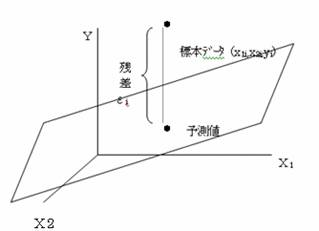
説明変量（ｘ₁，ｘ₂）と目的変量（ｙ）との間に相関関係があるとき

　　　　Ｙ＝ｂ₁･ｘ₁＋ｂ₂･ｘ₂＋ｂ₀

なる平面を考え、実際の標本データからこのこの平面上への残差をεとすると

説明変量が２つある時の重回帰式は

　　　　ｙ_i＝ｂ₁･ｘ_1i＋ｂ₂･ｘ_2i＋ｂ₀＋ε_i　と表される。

残差εに注目すると ε_i＝ｙ_i−Ｙ_i

ε_i＝ｙ_i−（ｂ₁･ｘ_1i＋ｂ₂･ｘ_2i＋ｂ₀）であるから

この残差平方和を求め、残差平方和が最小にするようなｂ₀・ｂ₁・ｂ₂ を求めると、重回帰式を得ることができる。

一般に説明変量がｐ個ある時の線形重回帰モデルは

　　　　ｙ_i＝β₁･ｘ_1i＋β₂･ｘ_2i＋…＋β_p･ｘ_pi＋β₀＋ε_i （i＝1,2 …ｎ）

と表される。この時単回帰分析と同様に

残差εについて、

　　�@ε_iとε_jはお互いに独立であり、正規分布　Ｎ（０，σ²）に従う。

　　�Aε_iの平均値（期待値）は０である。

　　�Bε_iの分散は一定である。　

との仮定下で重回帰予測式を

　Ｙ_i＝ｂ₁･ｘ_1i＋ｂ₂･ｘ_2i＋…＋ｂ_p･ｘ_pi＋ｂ₀ とする。

　ｂ₁･ｂ₂…ｂ_pを偏回帰係数といい、 β₁･β₂…β_p を母偏回帰係数という。

［残差平方和�煤iε_i）² を最小にするようなｂ₀･ｂ₁･ｂ₂ を求める。］

�煤iε_i）² ＝�煤oｙ_i−（ｂ₁･ｘ_1i＋ｂ₂･ｘ_2i＋ｂ₀）｝² を最小にするｂ₀･ｂ₁･ｂ₂ を 求める。

ｆ＝�煤iｙ_i−ｂ₁･ｘ_1i−ｂ₂･ｘ_2i−ｂ₀）² とし、この式をｂ₀･ｂ₁･ｂ₂で偏微分する。

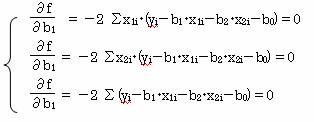
これより

　�狽�_1i･（ｙ_i−ｂ₁･ｘ_1i−ｂ₂･ｘ_2i−ｂ₀）＝０ …�@

　�狽�_2i･（ｙ_i−ｂ₁･ｘ_1i−ｂ₂･ｘ_2i−ｂ₀）＝０ …�A

　 �煤iｙ_i−ｂ₁･ｘ_1i−ｂ₂･ｘ_2i−ｂ₀）＝０　　　　 …�B

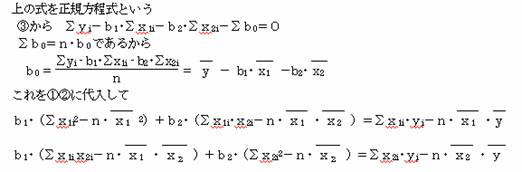
これよりｂ₀･ｂ₁･ｂ₂ を求めると、重回帰式の係数を得ることができる。

1.2.2　偏差平方和・積和から重回帰式を求める

　(1)説明変量が２個の時

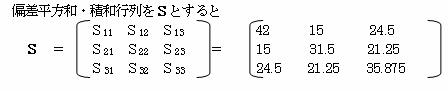
説明変量ｘ₁･ｘ₂ の偏差平方和それぞれＳ₁₁・Ｓ₂₂、偏差積和をＳ₁₂とすると

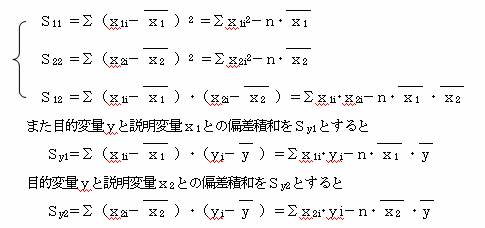
以上から前の式は

　　　　Ｓ₁₁･ｂ₁＋Ｓ₁₂･ｂ₂＝Ｓ_y1

　　　　Ｓ₁₂･ｂ₁＋Ｓ₂₂･ｂ₂＝Ｓ_y2

　　となるので、これから係数ｂ₀･ｂ₁･ｂ₂を求める。

　　　

(2)説明変量がｐ個ある時

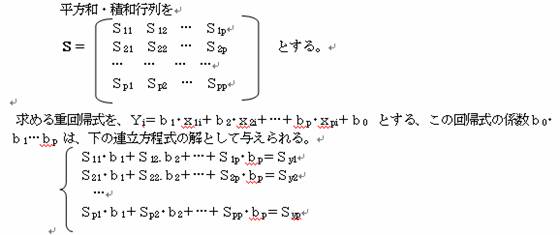
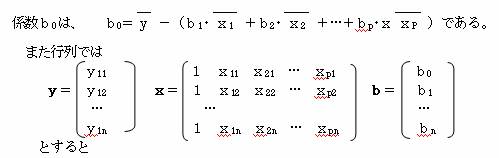
係数ｂは、 ｂ＝（ｘ’･ｘ）⁻¹･ｘ’･ｙ で求めることができる。

１．３　標準偏回帰係数

　説明変量がどれくらい目的変量に影響を与えているか（寄与しているか）を見るには、求めた重回帰式の偏回帰係数を見ればよい。通常、偏回帰係数が大きいほど目的変量に与える影響が大きいので多く寄与しているといえる。しかし、説明変量間で単位が異なるときには、単位の影響を受けるので、単純に偏回帰係数の大小比較して決めることはできない。単位の影響を除くには、標本データを標準化する。データを標準化することにより、平均＝０・分散＝１となり単位の影響を受けなくなるので、標準化したデータから偏回帰 係数を求めるようにする。このように標準化したデータから得られた偏回帰係数を、標準 偏回帰係数という。

標準偏回帰係数の大きいほど、目的変量に与える影響が大きく、寄与の大きい変量である といえる。

通常説明変量が２つの時の重回帰式は

１．４　相関係数と決定係数

1.4.1　単回帰式における相関係数と決定係数

説明変量ｘの変化に従って目的変量ｙが変化する（相関関係にある）ときｘとｙの間の相関係数をRとすると

いま説明変量ｘと実測値ｙとの関係がｒである時、これから求めた単回帰式を

　　　　Ｙ＝ｂ₁･ｘ＋ｂ₀ とすると

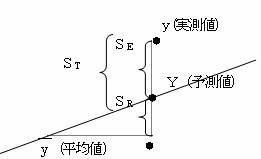
実測値ｙは、単回帰直線の付近にばらついて散在している。このばらつきの小さいほど単回　　帰式のあてはまりがよい（精度が高い）直線といえる。また説明変量ｘの目的変量に与える影響が大きいといえる。つまり決定力が大きいといえる。

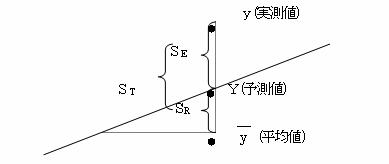
分散状況を見ると、全分散（Ｓ_T）は、実測値ｙ_iが平均値ｙからどれ位分散しているかであるので、回帰で説明可能な部分の分散（Ｓ_R）、つまり予測値が平均値からどれ位分散しているかは、回帰で説明できない残差部分の分散（Ｓ_E）つまり実測値が予測値からどれ位分散しているかは、�煤iｙ_i−Ｙ_i）²である。

　　これらの変動の間には、

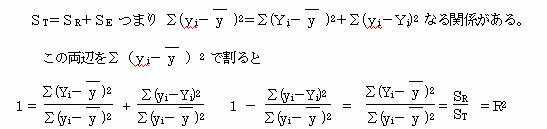このＲ² のことを決定係数という。この決定係数は　０≦Ｒ²≦１の値をとる。

また、この決定係数Ｒ²は相関係数Rの２乗に等しい。

1.4.2　重回帰式における相関係数と決定係数

（１）重相関係数と決定係数

重相関係数Rは、実測値データｙと重回帰式から求めた予測値データＹとの相関係数である。

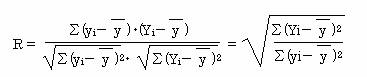
また単回帰のときと同様に、相関係数の２乗を決定係数と呼び、やはり０≦Ｒ²≦１の値をと　 る。Ｒ² が１に近いほど重回帰式の精度が高いといえる。

［重相関係数の検定］

標本から得られた重相関係数について、その母重相関係数（ρ）が無相関かどうかの検定を　　行う。標本から得られた重相関係数をRとする時、その母相関係数（ρ）についてρ＝０の仮説につき、検定統計量をＦとすると

は、自由度ｐ，ｎ−ｐ−１のＦ分布に従うことを利用して検定を行う。

検定をおこなう

　　(1)仮説をたてる

　　　 仮　　説　Ｈ₀：ρ＝０ （母重相関係数は無相関である）

　　　 対立仮説　Ｈ₁：ρ≠０ （母重相関係数は無相関ではない）

(2)検定統計量Ｆは自由度ｐ，ｎ−ｐ−１のＦ分布に従う。

　　(3)有為水準αで検定を実行する。

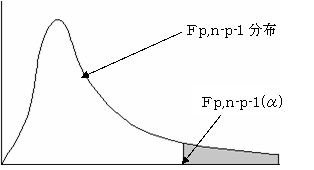
Ｆ≧Ｆp,n−p−1(α)であれば、仮説を棄却する。つまり、母重相関係数は有効であり、実測値と予測値の間には相関があるといえる。

重相関係数は、実測値ｙと予測値Ｙとの相関係数である。これに対して単純に２変量間の相関係数を単相関係数という。多変量データにおいて、２変量間の相関係数が本当に正しい相関を示すとは限らない。多変量においては２変量間の相関係数を求めても、その２変量以外の変量がこの２変量に影響を与えるからである。よって、多変量間における２変量の正しい相関係数を求めるには、相関係数を求める２変量以外の変量の影響を取り除いて（一定にして）相関係数を求める必要がある。このようにして求めた相関係数を偏相関係数という。

（２）偏相関係数

多変量データにおいて、任意の２変量間の単純な相関係数を単相関係数というが、これは相関をとる２変量以外の変量が、その２変量に影響を与えている相関係数である。これに対し、相関を求める２変量以外の他の変量の影響を取り除いた２変量間の相関係数を偏相関係数という。

いまＰ変量の任意の２変量間の単相関係数をｒ_ijとする。

	ｘ1 ｘ2 … ｘp
ｘ1 ｘ2 … ｘp	ｒ11 ｒ21 … ｒp1 ｒ21 ｒ22 … ｒp2 … ｒp1 ｒ2p … ｒpp

（３）自由度調整済み決定係数

　決定係数や重相関係数は、説明変量の数を増やすと単純に増加する傾向がある。

そこで、単純に説明変量の数を増やしても、決定係数が単純に増加しないように調整した自由度調整済み決定係数という。通常標本数がｎ個、説明変量がｎ−１個のものは分析することができない。必ず説明変量がｎ−２個以下にする必要がある。

自由度調整済み決定係数をＲ’² とすると

１．５　回帰式の信頼性

　回帰式を使用して説明変量から目的変量の値を予測する時、その予測値がどのくらい信頼性があるのかを検定する方法に、分散分析を用いる方法と相関係数を用いる方法がある。

1.5.1　分散分析を用いる場合

（１）単回帰のとき

　　　説明変量ｘと実測値ｙと単回帰式から求めた予測値Ｙが下表のようである時

標　本	説明変量ｘ	実測値ｙ	予測値Ｙ
１ ２ … ｎ	ｘ1 ｘ2 … ｘn	ｙ1 ｙ2 … ｙn	Ｙ1 Ｙ2 … Ｙn

予測値Ｙiは、Ｙ＝ｂ₁･ｘ＋ｂ₀の回帰式から求めた値

以上のデータをもとに、分散分析表を作成し回帰式の信頼性を検定する。

　全体の変動（Ｓ_T）を、回帰による変動（Ｓ_R）と残差による変動（Ｓ_E）とに分け、回帰による変動が残差による変動よりも小さいようであれば、回帰直線で求めた予測値は残差による影響の方が大きいので予測には役立たないと考える。

実測値の変動（Ｓ_T）＝回帰による変動（Ｓ_R）＋残差による変動（Ｓ_E）

　 残差が小さいほど｢実測値の変動｣≒｢回帰による変動｣となり、よい予測値を得られる。

　　

(1)変動を求める

　�@実測値の全変動（Ｓ_T）…実測値の各値ｙ_iが、実測値の平均からどれ位ばらついているかである。　

右片側検定を行い、Ｖ_RがＶ_Eより大きいかどうか検定する。Ｖ_R＞Ｖ_Eであれば、回帰による変動が残差による変動よりも全変動に与える影響が大きいので、回帰直線は予測に役立つといえる。

(5)検定を行う

　(1)仮説をたてる

仮　　説 Ｈ₀：回帰直線は予測に役立たない（Ｖ_R≒Ｖ_E）

対立仮説 Ｈ₁：回帰直線は予測に役立つ（Ｖ_R＞Ｖ_E）

(2)検定統計量Ｆを求める

は自由度１，ｎ−２のＦ分布に従う

(3)有為水準αで右片側検定を行う

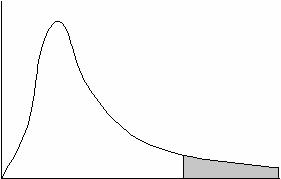
Ｆ1,n-2 分布

↑

Ｆ1,n-2 (α)

Ｆ≧Ｆ1,n-2 (α)であれば、仮説Ｈ₀を棄却し、対立仮説Ｈ₁：回帰直線は予測に役立つを採択する。つまり、この回帰直線は予測に役立つとする。

以上をまとめて分散分析表を作成する。

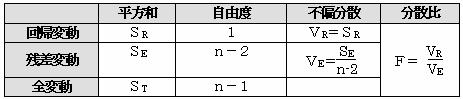
分散比Ｆは自由度１，ｎ−２のＦ分布に従う

（２）重回帰のとき

　説明変量がＰ個ある時の多変量データが下のようになっているとする

予測値はＹ＝ｂ₁･ｘ_1i＋ｂ_2･ｘ_2i＋…＋ｂ_p･ｘ_pi＋ｂ₀ から得た値

　　　　　ｎ：標本数　　ｐ：説明変量の個数

単回帰同様に、全体の変動を回帰による変動と残差による変動とに分け、分散分析表を作成し重回帰式の信頼性を検定する。

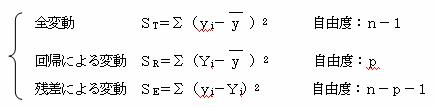
変動の関係 Ｓ_T＝Ｓ_R＋Ｓ_E

以上をまとめて、分散分析表を作成すると

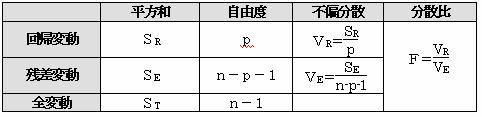
分散比Ｆは、自由度ｐ，ｎ−ｐ−１のＦ分布に従うので、これを利用して単回帰の場合と同様に回帰式の信頼性を検定することができる。

分散分析では、回帰式の信頼性を検定することはできるが、どれ位信頼できるかについては不明である。

1.5.2　相関係数を用いる場合

　相関係数Rの２乗は決定係数と呼ばれているが、この決定係数を利用して回帰式の信頼性を見る。

　

となり、分散分析のＦ値が重相関係数の検定の検定統計量と一致する。

１．６　標準誤差（ＳＥ：Standard Error）

　標準誤差とは、推定値の標準偏差（ＳＤ）をいう。

　　いま、標本ｎ₁個から得られた回帰式を　Ｙ₁＝ｂ₁₁･ｘ₁₁＋ｂ₂₁･ｘ₂₁＋…＋ｂ_p1･ｘ_p1

　　次の標本ｎ₂個から得られた回帰式を　　Ｙ₂＝ｂ₁₂･ｘ₁₂＋ｂ₂₂･ｘ₂₂＋…＋ｂ_p2･ｘ_p2

以下同様にしてこれを何回か繰り返すと係数ｂ₁ は正規分布に従うことが分かっている。同様にｂ₂…ｂ_pについてもそれぞれ正規分布に従う。この時の標準偏差を標準誤差という。

1.6.1　標準誤差を求める

（１）単回帰の時

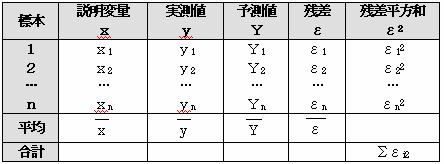
（２）重回帰の時

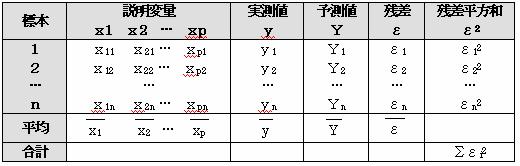
重回帰式をＹ_i＝ｂ₁･ｘ_1i＋ｂ₂･ｘ_2i＋…＋ｂ_p･ｘpi＋ｂ₀　とすると

残差はε_i＝ｙ_i−Ｙ_iで、残差平方和（Ｓ_E）は �買ﾃ_i²＝�煤iｙ_i−Ｙ_i ）²

自由度は、ｎ−ｐ−１

不偏分散は Ｖ_E＝Ｓ_E／（ｎ−ｐ−１）

説明変量の偏差平方和積和行列をＳであらわすと

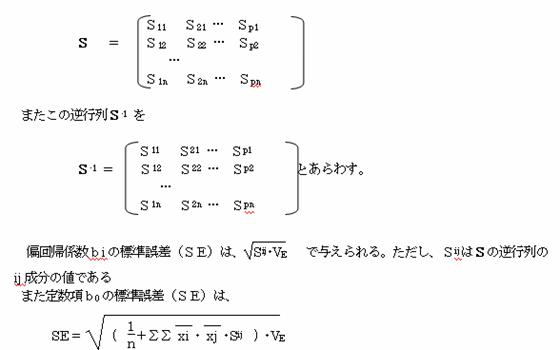
１．７　偏回帰係数の検定

標本から得られた回帰式の信頼性については、分散分析を行うことにより検定することができる。回帰式が予測に役立つとしたとき、次に偏回帰係数が有効かどうか検定し、有効でない偏回帰係数は予測結果に影響を与えていないので、使用しなくてもよい係数ということになる。

いま、重回帰モデルを、ｙ_i＝β₁･ｘ_1i＋β₂･ｘ_2i＋…＋β_p･ｘ_pi＋β₀＋ε_i （i＝1,2 …ｎ）とするとき

残差εについて、

　�@εiとεjはお互いに独立であり、正規分布　Ｎ（０，σ²）に従う。

　 �Aεiの平均値（期待値）は０である。

　 �Bεiの分散は一定である。　

との仮定下で重回帰予測式を

Ｙ_i＝ｂ₁･ｘ_1i＋ｂ₂･ｘ_2i＋…＋ｂ_p･ｘ_pi＋ｂ₀ とする。

母偏回帰係数β_i＝０を検定することにより、その偏回帰係数が予測結果に影響を与えうる係数かどうかの検定を行う。

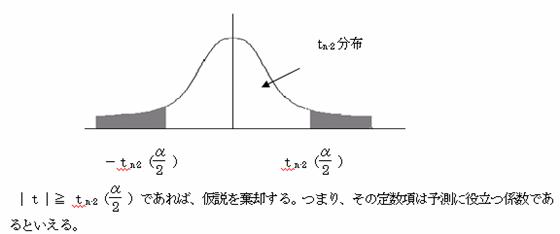
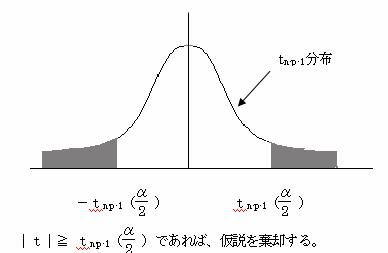
1.7.1　単回帰における回帰係数および定数項の検定

　　単回帰式を　Ｙ＝ｂ₁･ｘ＋ｂ₀ とする。

（１）回帰係数ｂ1の検定

　

(1)仮説をたてる

　 　 帰無仮説 Ｈ₀：β₁＝０ （説明変量ｘの母回帰係数は０である）

　　 対立仮説 Ｈ₁：β₁≠０ （説明変量ｘの母回帰係数は０でない）

(2)検定統計量ｔを求める

　 (3)有為水準αで両側検定を行う

(1)仮説をたてる

　 帰無仮説 Ｈ₀：β₀＝０

　 対立仮説 Ｈ₁：β₀≠０

(2)検定統計量ｔは、自由度ｎ−２のｔ分布に従う

(3)有為水準αで両側検定を行う

1.7.2　重回帰における偏回帰係数および定数項の検定

　　　重回帰式をＹ_i＝ｂ₁･ｘ_1i＋ｂ₂･ｘ_2i＋…＋ｂ_p･ｘ_pi＋ｂ₀ とする

（�T）偏回帰係数ｂ_iの検定

検定統計量をｔとする

　　

　ただし、ＳＥ：偏回帰係数ｂiの標準誤差

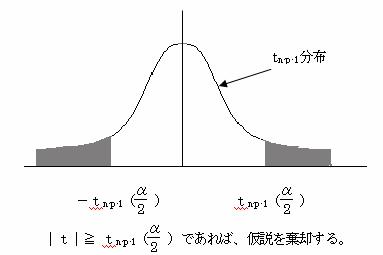
(1)仮説をたてる

帰無仮説 Ｈ₀：β_i＝０　（説明変量ｘ_iは予測に役立たない）

対立仮説 Ｈ₁：β_i≠０　（説明変量ｘiは予測に役立つ）

(2)検定統計量ｔは自由度ｎ−ｐ−１のｔ分布に従う

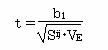
(3)有為水準αで両側検定を行う

（２）定数項ｂ₀の検定

検定統計量をｔとする

　　　　　

(1)仮説をたてる

帰無仮説 Ｈ₀：β₀＝０　（定数項は予測に役立たない）

対立仮説 Ｈ₁：β₀≠０　（定数項は予測に役立つ）

(2)検定統計量ｔは自由度ｎ−ｐ−１のｔ分布に従う

(3)有為水準αで両側検定を行う

１．８　多重共線性について

説明変量間においてお互いに高い相関がある時、偏回帰係数を求めることができないという現象を引き起こす。これを多重共線性という。説明変量間でお互いに高い相関があるということは、どちらも同じことを説明している変数なのでどちらか一方の変量があればよいといえる。重回帰式を求めるにあたり、多重共線性があるときにはどちらかの説明変量を落として求める必要がある。　

多重共線性の有無については、

(1)説明変量間の単相関係数を求め、単相関係数が１または−１に近いものがあれば多重共線性がある。

(2)多重共線性が認められるときには、偏回帰係数を求められないとか、偏回帰係数の符号と、説明変量と目的変量の単相関係数の符号が一致しない等の現象を起こす。

多重共線性の例(1)

標本	説 明 変 量			目的変量
	ｘ1	ｘ2	ｘ3	ｙ
１ ２ ３ ４ ５ ６	5 5 7 5 8 12	4 4 5.6 4 6.4 9.6	8 5 6 2 7 14	32 36 48 44 52 70

上記表から、説明変量間の相関行列を作成すると

ｘ₁−ｘ₂の相関係数が１であり、偏回帰係数を求めることができない。

　 ｘ₂＝ｘ₁×0.8 となっており、ｘ2変量は目的変量ｙに何の寄与もしていないので不用な変量であるといえる。ｘ₁変量を使うとき、ｘ₂変量を落として回帰式を求めなければならない。

１．９　良い重回帰式を作成する

　重回帰式は、いくつかの説明変量から目的変量の値を予測するが、説明変量をむやみに多くしても無駄なことが多い。理想的な重回帰式は、なるべく少ない説明変量でなおかつ誤差の小さな目的変量を得られるような式である。このためには説明変量を調べ、回帰式に必要な変量であるかを検討する必要がある。

（１）説明変量の選択基準

(1)目的変量に与える影響の大きい説明変量を選ぶ。各説明変量と目的変量間の単相関係数を求め、各説明変量の目的変数に与える影響の大きさを調べる。

(2)説明変量間で高い相関が認められるときには、どちらか一方の変量を落として重回帰式を作成する。一般に説明変量間の単相関係数が０．９以上ある時にはどちらか一方の説明変量を落とす。特に説明変量間で単相関係数≒１の時には偏回帰係数を求めることができない。

(3)偏回帰係数≒０となるような説明変量は、役にたたない変量であるから落とすようにする。

（２）重回帰式の良さを評価する方法

　いくつかの説明変量を使用して何種類かの重回帰式を作成したとき、それらの重回帰式の中で、どの重回帰式が一番よい回帰式であるかを判断する基準としてＡＩＣ（赤池の情報量基準）がある。ＡＩＣは

ＡＩＣ＝ｎ･（ｌｏｇ_e２π＋１）＋ｎ･ｌｏｇe･ ＋２･（ｐ＋２）

で与えられる。

　但しｎ：標本数　ｐ：説明変量の個数　Ｓ_E（残差平方和）：�煤iｙ_i−Ｙ_i）²

　ＡＩＣの値は小さいほど当てはまりがよいとされているが、絶対的基準を与えるものでは　　　ないので、どの値以下が良いとはいえない。あくまでの、いくつかの説明変量を組み合わせて作成した回帰式のそれぞれのＡＩＣ値を求め、それらの回帰式の中でＡＩＣ値が最も小さいものが一番良い回帰式であると判断する。

１．１０　変数選択法

　説明変量がいくつかある時、どの変量を使用すれば最良の重回帰式を得ることができるかを解決するために、変数選択法がある。

（１）総あたり法

　説明変量がＰ個あるとき、このＰ個の全ての組合せ（２P−１通り）について回帰式を作成し、回帰式の検討する方法。この方法では説明変量の個数が増えると作成する回帰式が膨大になり、実用的ではない。

（２）逐次選択法（ステップワイズ法）

�@変数増加法…変数０から出発し、順次変数を増やしていく方法

�A変数減少法…全説明変量使用した回帰式から出発し、順次変数を減少させていく方法

　�B変数増減法…変数０から出発し、順次変数を増やしていくが、一度取り込んだ変数でもある基準を満たさなくなったときには落としてしまう方法

�C変数減増法…全説明変量使用した回帰式から出発し、順次変数を減少させていくが、一度落とした変量についてもある基準を満たすときには再度採用する方法

［偏回帰係数のＦ値を使用したステップワイズ法］

（１）変数増加法

　�@変数０から出発する。

　�A目的変量ｙと各説明変量ｘ₁…ｘ_pとの単相関係数を求め、この中で最も相関係数の大きい変数を取り込む。

または、単相関係数を求める代わりに、ｙ−ｘ₁　…　ｙ−ｘ_pと２変量ずつの回帰式を　　　　作成し、それぞれの偏回帰係数をみて、そのＦ値が最も大きく、なおかつＦ値が２以上（自由度に関係なく）の変数を取り込む。なお、全偏回帰係数のＦ値が２以下の時には取り込むべき変数はないとする。

いま、ｘ₁を採用するとするとＹ＝ｂ₁･ｘ₁＋ｂ₀の式ができる。

�B次に�Aで採用した変量以外の変量を１つ追加して回帰式を作成する。

　それぞれの回帰式について、その偏回帰係数のＦ値を求め、最大のＦ値を与えかつ自由度に関係なくその値が２以上のものがあれば、２番目の変量として採用する。

以下全変量についてこれを繰り返し実行する。

寄与率Ｒ² をそれぞれ求めて寄与率が最も大きいものを採用してもよいが、寄与率は、使用する変量の個数が増えると単純に増加する傾向があるので、寄与率が余り向上しないときには採用しない方がよい。

�C変数増加の打ち切り

　全ての変数について実行が終了し、もう取り込むべき変量がなくなったとき。

　または、最初に決めた打ち切りの決定値（Ｒ²）以下になったとき。

（２）変数減少法

�@最初全ての説明変量を使用した回帰式を作成し、それぞれの偏回帰係数のＦ値を求め、最小のＦ値でなおかつ２．０以下のものがあれば、その変量を削除する。

�A�@から１つ変量を減らした回帰式を作成し、それぞれの偏回帰式のＦ値を求め、最小のＦ値でなおかつ２．０以下のものがあれば、その変量を削除する。これを繰り返す。

　 または、寄与率Ｒ²を見ていき、その変量を削除しても余り寄与率の減少がみられないときには、その変量はなくてもよい変量なので削除する。

�B変数減少の打ち切り

　 全ての変量について実行が終了し、もう削除すべき変量がなくなったとき。

　　または、あらかじめ決めた決定値（Ｒ²）に達したとき。

（３）変数増減法

　　　変数増加法と似ているが、一度取り込んだ変数についても、その偏回帰係数のＦ値が２．０以下になるときには、回帰式から削除する。

（４）変数減増法

変数減少法に似ているが、一度削除した変数についても、再度取り込んでその偏回帰係数を調べその値が２．０以上になるときには再度取り込むようにする。

以上偏回帰係数を調べて変量の増加減少を行ってきたが、ＡＩＣ量を見ながら変量の増減をしていく方法がある。

偏回帰係数のＦ値と同様に、ＡＩＣ量を調べながら、�@変数増加法　�A変数減少法　�B変数増減法　�C変数減増法　がある。

　ＡＩＣ量を見ながらこれらの方法を行うときには、採否の基準とする偏回帰係数のＦ値は、自由度に関係なく

Ｆ＝（ｎ−ｐ−１）･（ｅ^2/n −１）　　を使用する。

ｎ：標本数　ｐ：説明変量の個数

１．１１　残差εについて

　回帰式において、残差εをみると

　残差εについての仮定は

　　　�@εi･εj はお互いに独立で、正規分布Ｎ（０，σ²）に従う。

　　　�Aεの期待値は０である。

　�Bεの分散は一定である。

　　以上の仮定下で線形重回帰モデルは

　　　　ｙ_i＝β₁･ｘ_1i＋β₂･ｘ_2i＋…＋β_p･ｘ_pi＋β₀＋ε_i （i＝1,2 …ｎ）とするとき残差εの分布は、ランダムでありかつ正規分布にしたがう。

いま、データが系時的に変化するとき、残差εは系時的に変化する。この残差の系時的変化を見ることにより、残差εのランダム性を調べることができる。

　残差εのランダム性を調べるには、下の２つの方法がある。

　　�@残差の系時的プロット図を作成し、その図から読み取る方法

　　�Aダービン･ワトソン比を求め調べる方法

1.11.1　残差プロットを見る方法

　　データが系時的に変化しているとき、その回帰式を求め、回帰式からのずれであるεを時系列に表示する。

　残差をみて、全体的傾向・＋−の出現状況・連の長さと数等を調べ、ランダム性を検討する。

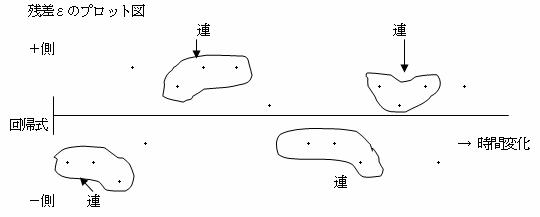
連…＋データ・−データが連続して現れるとき、それを連という。

　上のサンプルでの出現状況は、＋側：−側＝９：９＝１：１となっている。

（１）残差εの分布が＋側の分布と−側の分布が同様に分布しているかどうか調べるには、符号検定を行う。

標本	説明変量 ｘ1 ｘ2 … ｘp	実測値 ｙ	予測値 Ｙ	残差 ε	残差の符号 ＋・−
１ ２ … ｎ	ｘ11 ｘ21 … ｘp1 ｘ12 ｘ22 … ｘp2 … ｘ1n ｘ2n … ｘpn	ｙ1 ｙ2 … ｙn	Ｙ1 Ｙ2 … Ｙn	ε1 ε2 … εn

残差ε_i＝ｙ_i−Ｙ_iである。

「符号検定の実施」

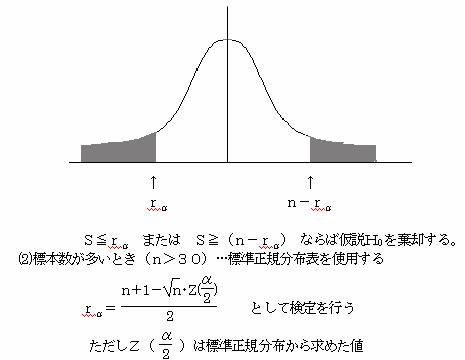
残差εを求める。この時ε＝０のものがｎ₀個あれば、標本数をｎ−ｎ₀個とする。

検定統計量Ｓは＋の符号の数とする。

(1)標本数が少ないとき（ｎ≦３０）…符号検定表を使用する

　�@仮説をたてる

　　仮　　説　Ｈ₀：μ₁＝μ₂ （２つの分布は等しい）

　　対立仮説　Ｈ₁：μ₁≠μ₂ （２つの分布は等しくない）

�A検定統計量Ｓは

　　 Ｓ＝残差の符号が＋の数

　�B有為水準＝αで両側検定を行う（符号検定表より上限・下限を求める）

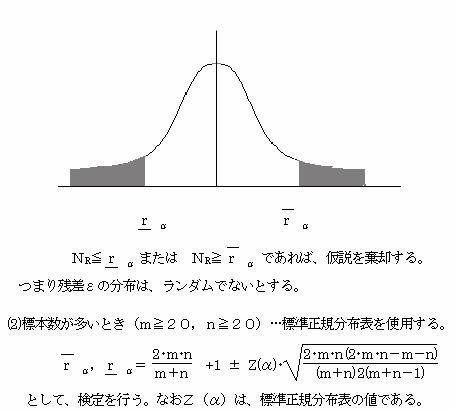
（２）残差εの分布が、ランダムに分布しているかの検定には、「連の数」による検定がある。

残差の「ある符号」の数をｍとし、「反対の符号の数」をｎとする。ｍ＋ｎ＝Ｎとする。

この時「＋の連」、「−の連」を合わせた全体の「連の数」をＮ_Rとする。

　　　　　　Ｎ_R＝「＋の連の個数」＋「−の連の個数」

(1)標本数が少ないとき（ｍ＜２０，ｎ＜２０）…連の数の検定表使用する。

�@仮説をたてる

　 仮　　説　Ｈ₀：残差εの分布はランダムである

　 対立仮説　Ｈ₁：残差εの分布はランダムでない

�A検定統計量Ｎ_Rは全体の連の数である

�B有為水準αで検定を行う（連の数の検定表から上限・下限を求める）

1.11.2　ダービン・ワトソン比を用いる方法

　　残差の連なりがランダムであるかどうかを検定するには、ダービン・ワトソン比を用いる方法がある。ダービン・ワトソン比をｄとすると

ダービン・ワトソン比とランダム性との関係は

�@残差が全くランダムである時…ｄ≒２

　�A残差に正の自己相関がある時…ｄ→０に近づく

　�B残差に負の自己相関がある時…ｄ→４に近づく

という性質を持っている。

自己相関とは、系時的残差変化間の相関をいう

残差εの自己相関を検定する

（１）正の自己相関があるか　

(1)仮説

帰無仮説 Ｈ₀：ρ＝０　（自己相関はない）

　　対立仮説　Ｈ₁：ρ＞０ （正の自己相関がある）

(2)検定統計量はｄ比である。

(3)有為水準αで検定を行う

　　　　 ｄ＜ｄ_Lならば、仮説Ｈ0：ρ＝０を棄却する。ρ＞０を採択。

　　　　　　ｄ＞ｄ_Uならば、仮説Ｈ1：ρ＝０を採択する。

ｄ_U＜ｄ＜ｄ_Lならば、ρ＝０　ρ＞０のどちらともいえない。

（２）負の自己相関があるか

　　負の自己相関を検定するときには、ｄの代わりに４−ｄとして検定を行う。

　(1)仮説

帰無仮説 Ｈ₀：ρ＝０　（自己相関はない）

　　　対立仮説　Ｈ₁：ρ＜０ （負の自己相関がある）

(2)検定統計量はｄ比である。

　 (3)有為水準αで検定を行う

　　 ｄ＞４−ｄ_Lならば、仮説Ｈ0：ρ＝０を棄却する。ρ＜０を採択。

　　 ｄ＜４−ｄ_Uならば、仮説Ｈ1：ρ＝０を採択する。

４−ｄ_U＜ｄ＜４−ｄ_Lならば、ρ＝０　ρ＞０のどちらともいえない。

（３）正・負どちらか不明の時

(1)仮説

帰無仮説 Ｈ₀：ρ＝０　（自己相関はない）

　　対立仮説　Ｈ₁：ρ≠０ （自己相関はない）

(2)検定統計量はｄ比である。

　 (3)有為水準αで検定を行う

　　ｄ≦ｄ_Lまたはｄ＞４−ｄ_Lなら仮説ρ＝０を棄却する。（ρ≠０を採択）

ｄ_U＜ｄ＜４−ｄ_Uなら仮説ρ＝０を採択する。

その他は不明

２．　重回帰分析例題

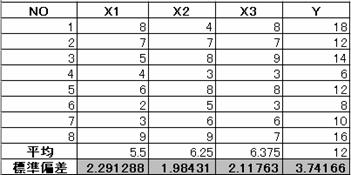
　ある会社の８店舗について、その店舗ごとの店員の充実度（Ｘ₁）・売り場面積（Ｘ₂）・商品充実度（Ｘ₃）を１０点評価で調査し、またそれぞれの店の月平均売上高について調べて表にしたものが下の表である。

ＮＯ	店員充実度	売り場面積	商品充実度	売上高（百万円）
	Ｘ1	Ｘ2	Ｘ3	Y
１ ２ ３ ４ ５ ６ ７ ８	８ ７ ５ ４ ６ ２ ３ ９	４ ７ ８ ３ ８ ５ ６ ９	８ ７ ９ ３ ８ ３ ６ ７	１８ １２ １４ ６ １２ ８ １０ １６

以上の表をもとにして、Ｘ₁〜Ｘ₃の３要素と売上高（Y）との間に何らかの関係があるかを重回帰分析を実行し調べる。

　重回帰分析を実行するには、まず分析用のデータをシートに入力しておく。データを入力後、重回帰分析を実行する。

　目的変量は売上高（Y）であり、説明変量はＸ₁〜Ｘ₃の３変量である。

２．１　重回帰式を求める。

重回帰式を、Ｙ＝ｂ₁･ｘ₁＋ｂ₂･ｘ₂＋ｂ₃･ｘ₃＋ｂ₀ とする。

2.1.1　偏差平方和・偏差積和を求める

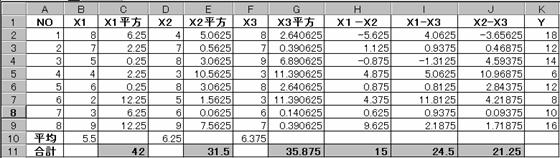
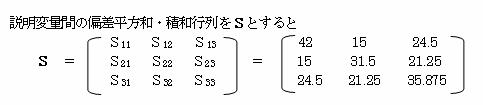
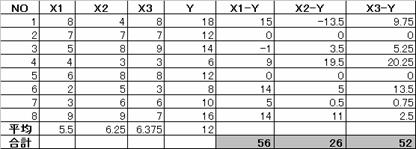
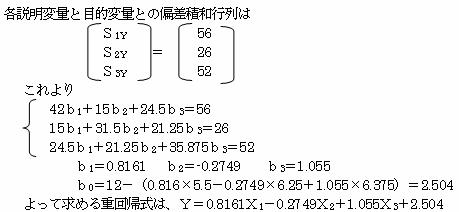
2.1.2 標準偏回帰係数を求める。

母集団に対する標準偏差を、関数　＝STDEVP(範囲)で求める。

＝STDEVP(範囲)で求めた標準偏差

　標準偏回帰係数の値から、目的変量に与える影響は変量Ｘ₃が最も大きく、次に変量Ｘ₁である。

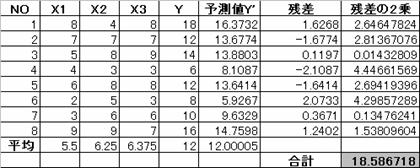
2. 1.3 予測値と残差を求める。

　　予測式は、Ｙ＝0.8161Ｘ₁−0.2749Ｘ₂＋1.055Ｘ₃＋2.504

2.1.4　偏回帰係数の標準誤差（ＳＥ）を求める。

残差平方和（Ｓ_E）は、Ｓ_E＝18.587 また不偏分散Ｖ_E＝18.587÷4＝4.647

その逆行列Ｓ^-1 を求める。

(1)＝MINVERSE(範囲)関数で、先頭の値を求める。

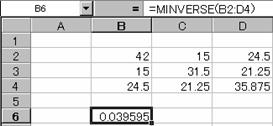
(2)求めた先頭の値を展開する。

2.1.6 重相関係数の値を見ると非常に正の相関が高そうである。そこで母相関係数をρとして、無相関の検定を行う。

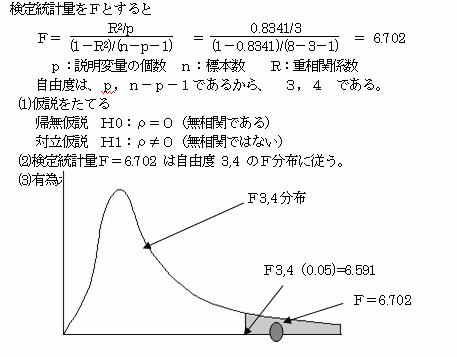
Ｆ＝6.702＞Ｆ3,4（0.05)=6.591 であり棄却域にはいる。よって帰無仮説Ｈ₀：ρ＝０を棄却する。母相関係数≠０であり、相関があるといえる。

２．７　自由度調整済重相関係数を求める。

　　

２．８ 求めた重回帰式の信頼性を検定する。

　　　　全変動（Ｓ_T）＝112　　 自由度：8-1=7

回帰による変動（Ｓ_R）＝93.4163 自由度：3

残差による変動（Ｓ_E）＝18.5867 自由度：8-3-1=4

以上から分散分析表を作成すると

	平方和	自由度	不偏分散	分散比
回帰変動	93.4163	3	31.1388	Ｆ＝6.701
残差変動	18.5867	4	4.6467
全変動	112	7

無相関の検定と同様の結果を得られる。求めた重回帰式は予測に役立つといえる。

2.8.1 偏回帰係数の信頼性を検定する

求めら重回帰式は信頼性があると検定で明らかになったので、次に重回帰式の偏回帰係数の有効性を検定する。偏回帰係数ｂiを検定する。

　検定統計量をＦとすると

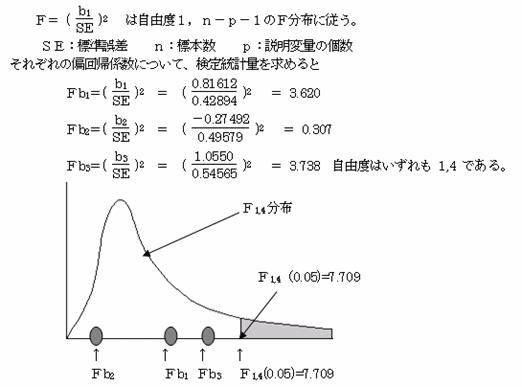
いずれも棄却域に入いらない。帰無仮説（母偏回帰係数β₁･β₂･β₃＝０）を棄却できない。

　　重回帰式は信頼性があるが、それぞれの偏回帰係数の有効性があるといえない。

2.8.2 偏相関係数を求める

　　偏相関係数は、説明変量Ｘiと目的変量との相関係数であり、他の説明変量の影響を取り除いたものである。どの説明変量が、目的変量と一番関係が深いかを知ることができる。　

　説明変量Ｘiと目的変量との偏相関係数を求める。

単相関係数行列をＲとすると

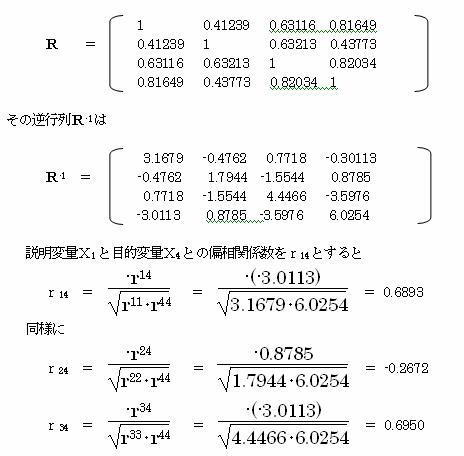
偏相関係数を見ると、ｒ₃₄＝0.6950 であり、変量Ｘ₃ と目的変量の関係が一番深いことが分かる。

２．９　回帰分析ツールの使用

2.9.1　Excelには、分析用ツールとして回帰分析ツールが備わっている。この回帰分析ツールを使用すえると、分析したいデータの入力されている範囲を指定するだけで、回帰分析を実施してくれる。

(1)データ入力後 → ツール → 分析ツール → 回帰分析をクリックして選択

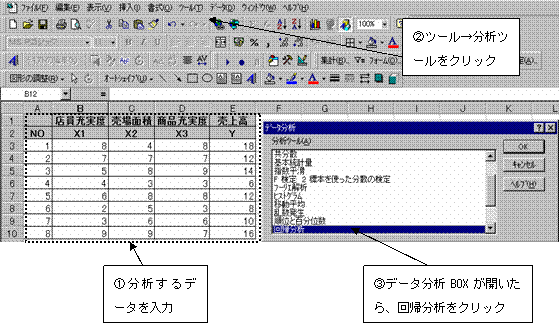
(2)分析するデータの範囲を指定

　入力Yは目的変量のデータ範囲を指定（常に1列データ範囲）、入力Xは説明変量範囲（連続した列の範囲）先頭行をラベルとして使用する時は、ラベルの項目をクリック。分析結果を表示する位置を指定する。また何の分析を実施するかをクリックしてチェックする。すべての指定が終了したら、OKボタンをクリック。

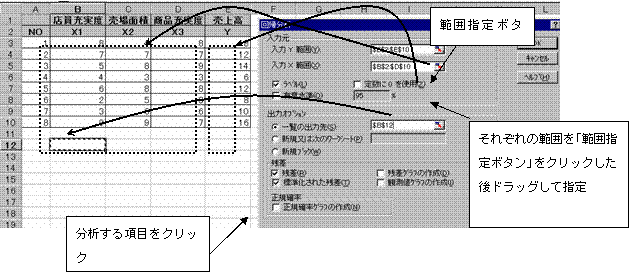
(3)一覧の出力先として指定したセル（B12)以降に分析結果が表示される。

概要
回帰統計
重相関 R	0.91326
重決定 R2	0.83405
補正 R2	0.70958
標準誤差	2.15562
観測数	8
分散分析表
	自由度	変動	分散	観測された分散比	有意 F
回帰	3	93.413	31.138	6.701077754	0.04869
残差	4	18.587	4.6467
合計	7	112
	係数	標準誤差	t	P-値	下限 95%	上限 95%	下限 95.0%	上限 95.0%
切片	2.50414	2.7503	0.9105	0.41406029	-5.1319	10.1401	-5.1319	10.1401
X1	0.81612	0.4289	1.9027	0.129839733	-0.3748	2.00704	-0.3748	2.00704
X2	-0.2749	0.4958	-0.555	0.6087767	-1.6515	1.10163	-1.6515	1.10163
X3	1.05497	0.5457	1.9334	0.125323541	-0.46	2.56996	-0.46	2.56996
残差出力
観測値	予測値: Y	残差	標準残差
1	16.3732	1.6268	0.9984
2	13.6773	-1.677	-1.029
3	13.8801	0.1199	0.0736
4	8.10878	-2.109	-1.294
5	13.6413	-1.641	-1.007
6	5.9267	2.0733	1.2724
7	9.63282	0.3672	0.2253
8	14.7597	1.2403	0.7611

上記分析結果から重回帰分析の結果を検討するようにする。

2.9.2　標準偏回帰係数を求める

　分析するデータを標準化して、その標準化されたデータについて回帰分析を実施すると、標準偏回帰係数を求めることができる。

(1)分析するデータを標準化する。

データを標準化するには、（X - )/δ　δ:標準偏差　で各データを標準化する。

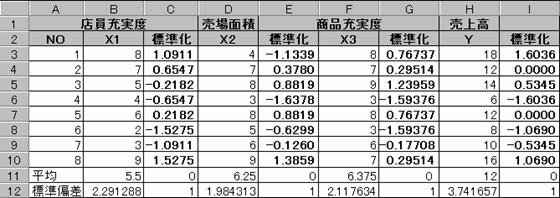
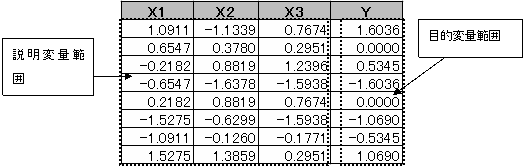
(2)標準化されたデータのみ、値複写で新しい表を作成する。

　元の表で標準化されたデータを、形式指定複写の値複写で標準化データのみの新しい表を作成する。

(3)標準化されたデータの表を使用して、回帰分析を実施

概要
回帰統計
重相関 R	0.91326
重決定 R2	0.83405
補正 R2	0.70958
標準誤差	0.57611
観測数	8
分散分析表
	自由度	変動	分散	観測された分散比	有意 F
回帰	3	6.672377	2.224126	6.701078	0.048686
残差	4	1.327623	0.331906
合計	7	8
	係数	標準誤差	t	P-値	下限 95%	上限 95%	下限 95.0%	上限 95.0%
切片	2.7E-18	0.203687	1.33E-17	1	-0.56553	0.565526	-0.56553	0.565526
X 値 1	0.49977	0.262668	1.902661	0.12984	-0.22952	1.229053	-0.22952	1.229053
X 値 2	-0.1458	0.262934	-0.5545	0.608777	-0.87582	0.584226	-0.87582	0.584226
X 値 3	0.59707	0.30882	1.933406	0.125324	-0.26035	1.454496	-0.26035	1.454496

　標準化されたデータを使用して、回帰分析を実施すると標準偏回帰係数が求められる。この係数を使用すると、目的変量の値も求めることができる。標準偏回帰係数を見ると、X₃の係数が最も大きく、目的変量に与える影響が一番大きい係数であることが分かる。もっとも元のデータにおいて、説明変量間の単位が同じであるから、標準偏回帰係数を求めなくても通常の偏回帰係数を見るだけで、どの説明変量が目的変量に与える影響が一番大きいかが分かる。

残差出力
標準偏回帰係数を使用した、予測値が求められる 観測値	予測値: Y	残差	標準残差
1	1.16878	0.434783	0.998353
2	0.44829	-0.44829	-1.02937
3	0.50249	0.032035	0.073559
4	-1.04	-0.56359	-1.29413
5	0.43865	-0.43865	-1.00723
6	-1.6232	0.554112	1.272357
7	-0.6327	0.098133	0.225334
8	0.73757	0.331472	0.761129

標準偏回帰係数を使用した予測式は、　Y = 0.49977 X₁ - 0.1458X₂ + 0.59707X₃ である。

この予測式を用いて予測値が計算されて求められる。

(4) 求められた予測値を更に標準化する。

NO	X1	X2	X3	Y	予測値: Y	標準化
1	1.0911	-1.1339	0.7674	1.6036	1.168784	1.27979
2	0.6547	0.3780	0.2951	0.0000	0.448290	0.49087
3	-0.2182	0.8819	1.2396	0.5345	0.502487	0.55021
4	-0.6547	-1.6378	-1.5938	-1.6036	-1.039973	-1.13875
5	0.2182	0.8819	0.7674	0.0000	0.438651	0.48031
6	-1.5275	-0.6299	-1.5938	-1.0690	-1.623157	-1.77732
7	-1.0911	-0.1260	-0.1771	-0.5345	-0.632656	-0.69274
8	1.5275	1.3859	0.2951	1.0690	0.737573	0.80762
平均	0.0000	0.0000	0.0000	0.0000	0.0000	0.00000
標準偏差	1	1	1	1	0.9132618	1.00000

2.9.3　重回帰分析に関する関数を使用して、重回帰分析を実施

(1)各変量の係数とY切片および重回帰式の検定を実施する関数：＝＝LINEST関数

＝LINEST関数：＝＝LINEST(既知目的変量Yの範囲、既知説明変量Xの範囲,,TRUE)

�@＝LINEST関数で、説明変量の商品充実度(X₃変量)の係数を求める。

　関数を使用するセル位置をクリックした後、関数のアイコンをクリックし、LINEST関数をクリック指定する。

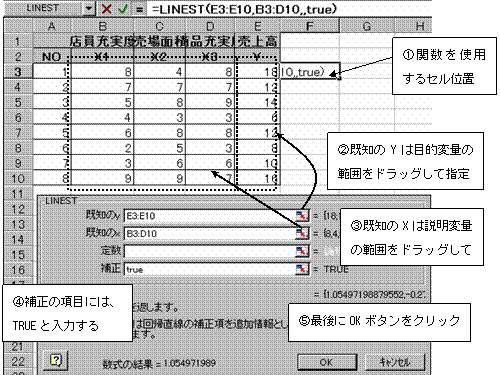
�A先頭のX₃の係数が求まったら、配列式を作成

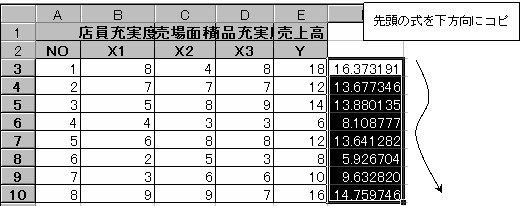
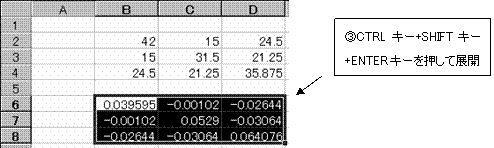
　現在分析に使用する説明変量は３つ、よって係数は説明変量分の３つとY切片の計4つの係数が必要であるから、配列指定は先頭のセルから横方向に4列分、また縦方向には常に5行分の範囲が必要である。よって先頭セルから横方向に4列・縦方向に5行分の範囲をドラッグして指定する。次に数式バーをクリックしアクティブにした後、CTRLキー+SHIFTキー+ENTERキーを押して配列式を完成する

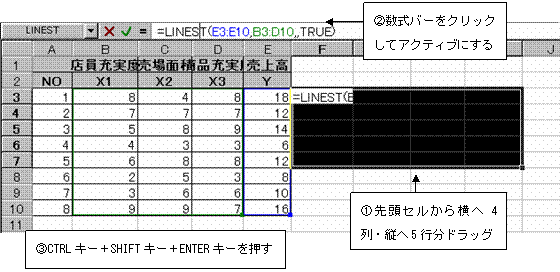
配列式が表示される

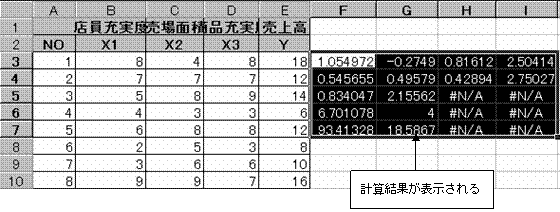
配列式に表示されているデータの意味

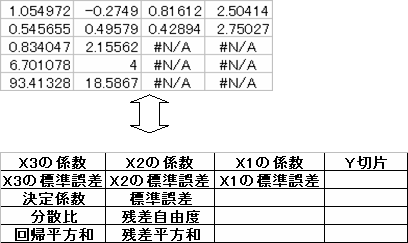
　これより、重回帰式は　Y=0.81612X₁−0.2749X₂＋1.054972X₃＋2.50414 である。

またこの重回帰式の信頼性は、分散比（F値)＝6.701078　であり、この値を使用して確率を求める関数で　＝FDIST(6.701078,3,4)=0.048686297　となり、求めた重回帰式は予測に役立たないという帰無仮説が棄却される。

(2)予測値を求める関数：＝TREND関数

　TREND関数を使用すると、重回帰式を使用して予測値を求めることができる。

TREND関数：＝TREND(既知目的変量Y範囲,既知説明変量X範囲,新しいX範囲)である。

�@既知目的変量Yの範囲および既知説明変量Xの範囲はドラッグして範囲指定後、F4キーを押して絶対座標にする。また新しいX範囲は、予測値を求めたいX₁･X₂･X₃の範囲をドラッグして指定する。こちらは相対座標のままでよい。このようにして式を作成すれば、下方向にコピーして一度に予測値を求めることができる。

関数を使用するセル位置をクリックした後、関数のアイコンをクリックし、TREND関数をクリック指定する。

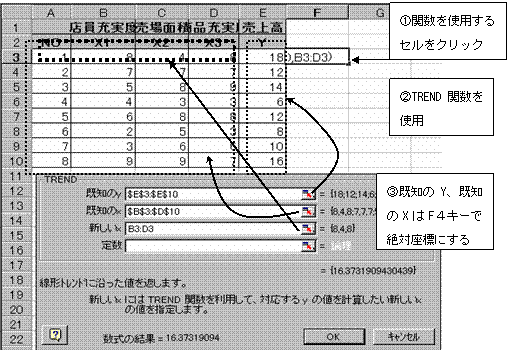
�A先頭の式が作成できたら、下方向にコピーして他の予測値を求める。

EXCEL多変量分析ホームページへ戻る