1.2. Magnus Effect

When you throw a ball with applying spin, the ball flies in an arc. This is because air flow changes by spin, the force acts in the direction perpendicular to the flight direction. The acting force is proportional to the cross product of the spin vector and velocity vector. This effect is called the Magnus effect taking the name of the discoverer. In the figures the magnitude of a spin is expressed by Magnus.

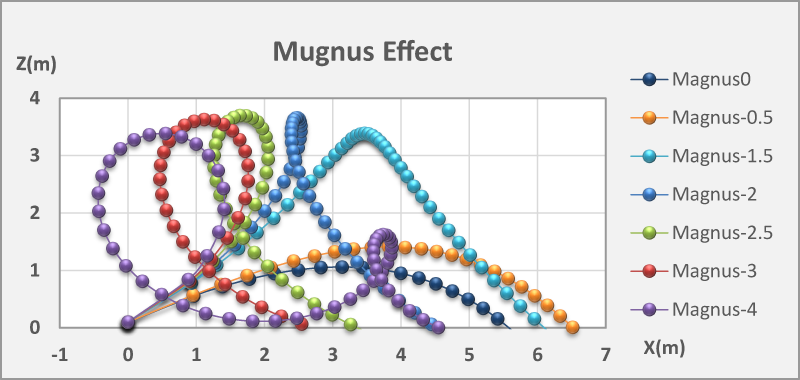
The left figure is the flight simulation results using the ball of table tennis. These flight trajectories are compared changing the speed of backspin, but the initial velocity is all the same. "Magnus -0" indicates the ball flight trajectory at the zero spin, it steps up to the speed "Magnus -4".

I remember that I was very surprised. The team coach I was a member launched it over with backspin on the ball. The ball was just flying like the "Magnus -4". And the ball rised again against the gravity.

Let's return to talking about the general motion of the ball.

We say non spin ball a knuckle. This flight is very unstable. Increasing the ball speed, their flight distance become more longer. However, the force adjustment to put in the coat becomes more difficult.
The knuckle has less spin momentum, so the ball will have less repulsion from the opponent racket when the opponent receives it.

Topspin is called Drive. If you apply top spin, the ball will bend downward. By this fact, even if the ball fly fast, you will be able to enter the ball into the coat easily.

The ball stays longer in the air when you give a backspin. If you do not care, the ball will jump off from the table end. Players for the chop swing use this spin in the hitting from a distance.

The following figure shows these relationships. Each flight trajectories is the same initial velocity.

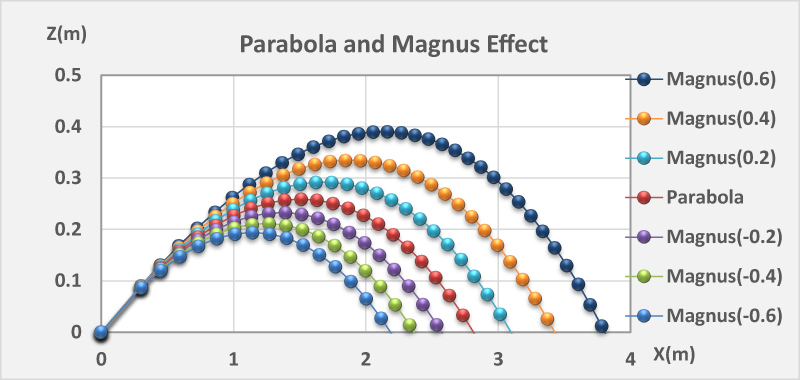
ωy = 0, the flight trajectory of none spin.
ωy = -0.2 ~ -0.6, the flight trajectories of drive spin.
ωx = 0.2 ~ 0.6, the flight trajectories of cut spin.

Let us show the height of the ping-pong table size and net for reference, since it is necessary to access those information in some articles also from hereafter.

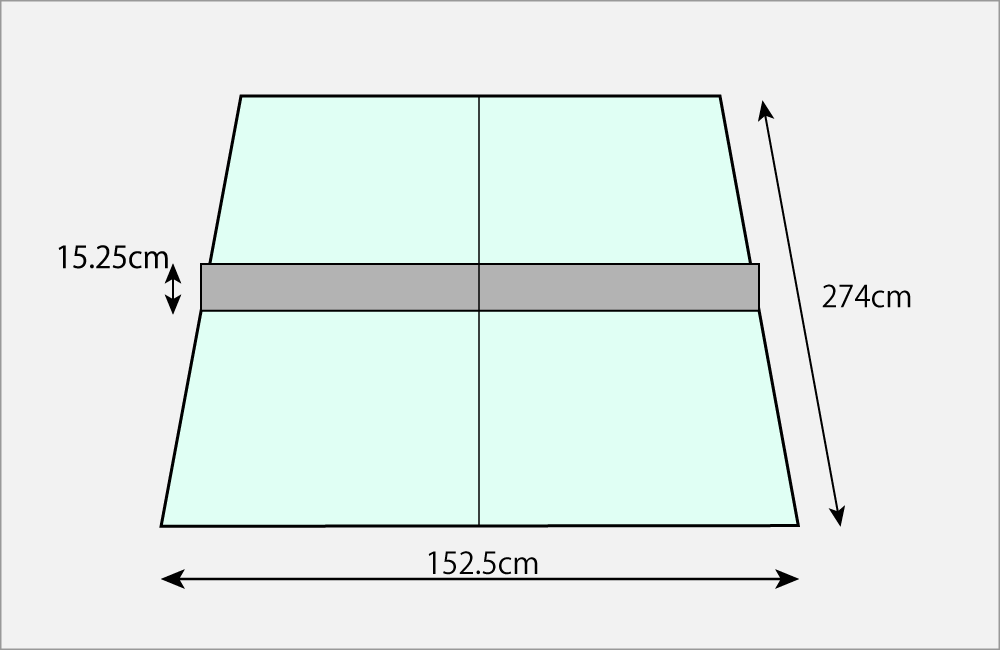
Lateral size of the table is 10 times the net height. On the other hand, the longitudinal size which is the table edge from the net is 9 times the net height. It is 18 times in the total size. The longitudinal size is longer than which from your eye level.