1.2 マグナス効果

球に回転をかけながら投げると曲がる。これは回転によって空気の流れが変化し、 飛びの方向と直角方向に力が作用するためだ。回転をω(オメガ)とすると、作用する力は、 回転ベクトルと速度ベクトルの外積に比例する。 この効果を、発見者の名前をとってマグナスの効果と呼ばれている。

Fig-1.2.1

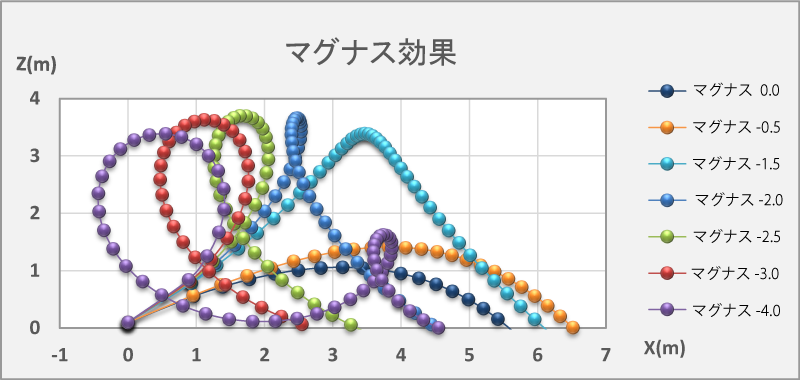
左の図は同じ初速なのだが、下回転の速度を変えたときの卓球の球のシミｭレーション結果である。 マグナス０が無回転の時の球の軌道を示し、マグナス－４まで下回転速度を上げている。
私が所属していたチームのコーチが球に下回転を掛けて打ち上げたとき、 ちょうど下図のマグナス－４の様に、重力に逆らい球が再上昇したので、大変、驚いたことを覚えている。

普通の卓球の球の運動に戻ろう。

回転していない球をナックルという。球が回転してないと球の飛びは不安定だ。 速度を上げると、その分、遠くへ飛んでいくが、コートに入れる手加減が難しい。
ナックルは回転の運動量が少ないので、レシーブをした時に弾みが悪いのが特徴だ。

上回転の球をドライブという。上回転をさせると、球は下方に曲がる。 これによって、飛びの速い球でも、容易にコートに入るのだ。

下回転させると、球は上に長く留まろうとする。 注意しないと球はコートエンドから飛び出してしまう。 カット打ちの人は遠くから、この回転を利用した打ち方をしている。

この関係を示したのが次の図である。飛びの初速度はいずれも同じだ。

Fig-1.2.2

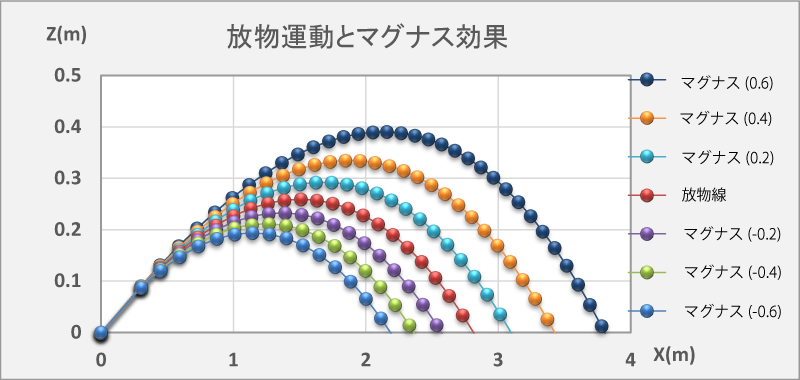
ωｙ＝０が無回転の球の軌跡で放物線を描く。
ωｙ＝－０．２～－０．６がドライブの球の軌跡。
ｗｘ＝０．２～０．６が下回転の球の軌跡だ。

これから先の記事でも必要になるので、参考までに卓球台の大きさとネットの高さをしめしておこう。

Fig-1.2.3

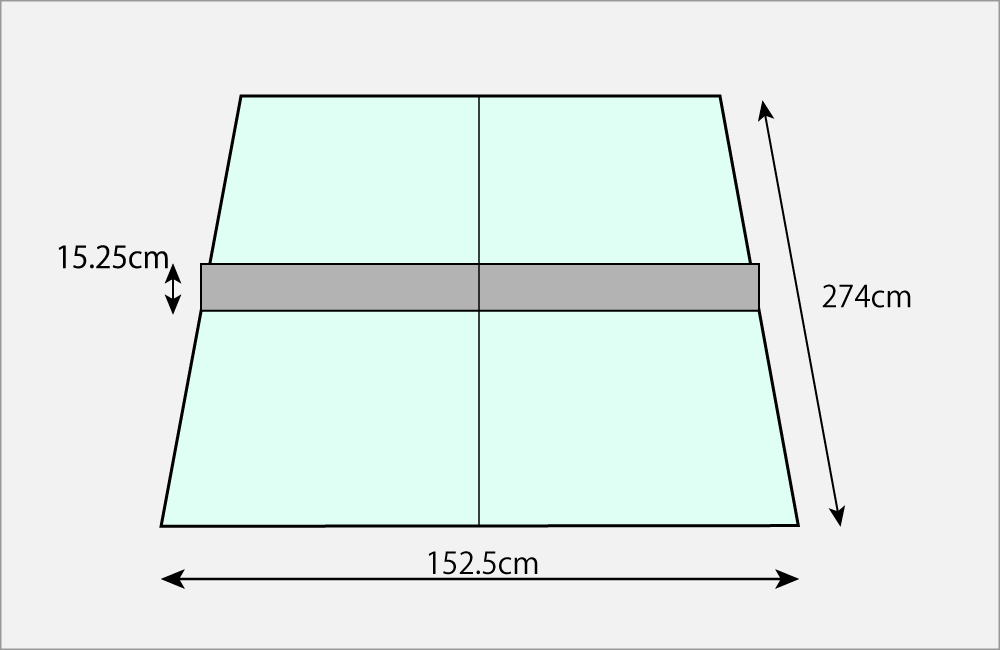
台の大きさはネットの高さに対して、横方向は１０倍であり、縦方向は、ネットからテーブルエンドまでは９倍であり、全体で１８倍だ。 目線で見たより縦に長い。