1.9. Relation of Swing and Ball
The force of swinging the racket is transmitted to the ball, and the ball flies and the ball rotates. The swing radius of the racket is the main factor of the power of the racket. The momentum that represents the momentum of a ball that receives power from a racket includes flight momentum and rotation momentum.
1.9.1. Relation between racket swing and flight distance
When playing table tennis, there are times when you really want to control the flight distance of the ball. It is essential to use short balls or long balls to make a good service. In addition, it is not enough to hit the ball fast even in defense and attack, and it is required to hit the ball short aiming at the side.
Since to the ball can be transmitted force through the racket, it is necessary to understand the relation between the swing of the arm and the momentum of the racket.
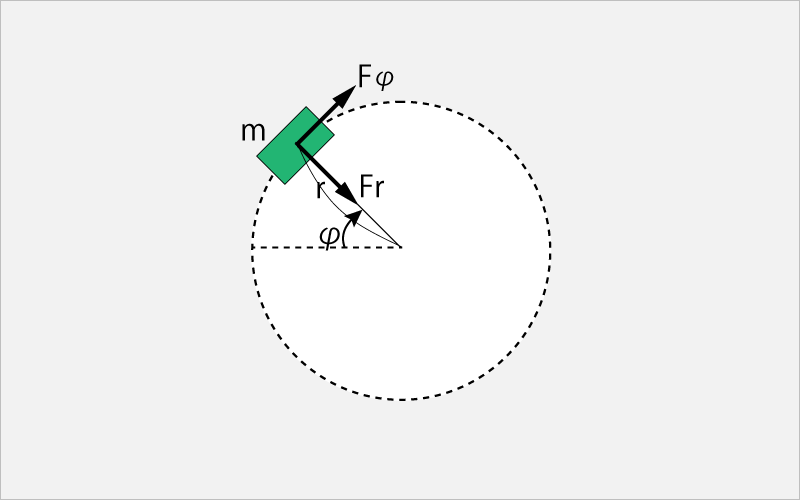
There is an equation representing the tangential force component in the equation of motion of circular motion.
Explaining in the following figure, if an object with mass m moves with a radius r and an angular acceleration φ'', and the tangential component Fφ and the direction component Fr of the force applied to the object, the equation of motion in the tangential direction Is as follows.
mrφ'' = Fφ
That is,
Mass x Radius of rotation x Angular acceleration of object = Tangential force component.
Applying this to the racket swing,
Racket mass x Swing radius x Swing angular acceleration = Tangential force component
The circular motion equation shows that the tangentia force component Fφ is proportional to the swing-out radius of the racket.
To control the force component by swinging the racket, adjusting the swing-out radius of the racket is much easier than adjusting the angular acceleration of the swing.
The radius of swing in this case refers to the XY plane, that is, the radius projected on the table.
The swing radius can be set by standing the racket or the elbow, or also rotating it around the midpoint between the wrist and arm joints.
It should be noted that the force in the radial direction Fr does not need to be considered here because it is naturally applied when the arm is rotated.
<Specific example>
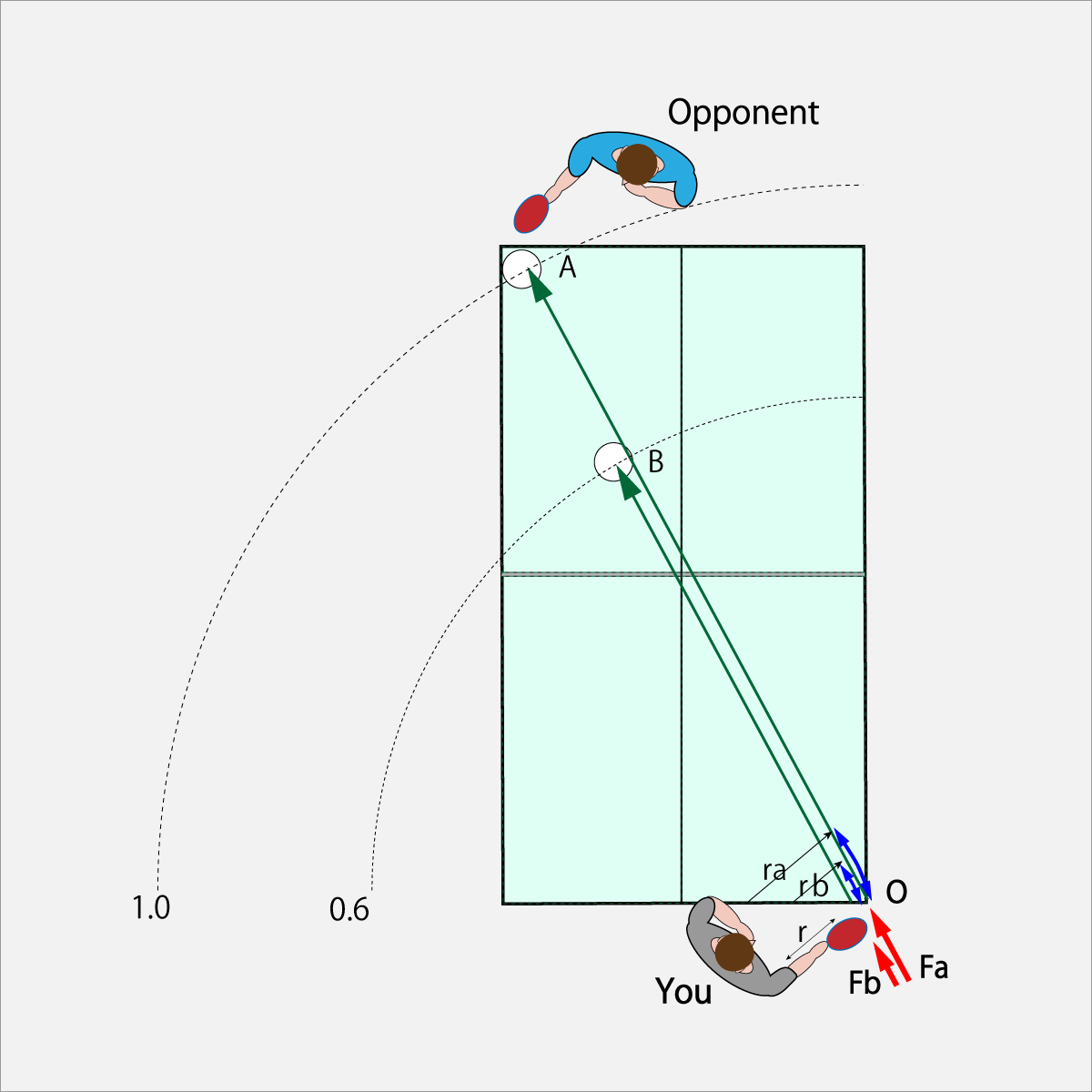
Look at the following figure. This figure depicts a service. Therefore, it is assumed that there is no influence of the ball from the opponent.
The flight direction of the ball is the same for A and B, The rotational angular velocities of the racket swing in A and B are the same.
However, when to the point A the swing radius of the racket is ra=1.0 , when to the point B the swing radius is rb=0.6 .
Therefore, since the range of the tangential force F is proportional to the turning radius of the swing, when to the point A the force is Fa=1.0, when to the point B the force will be Fb=0.6.
And the flight distance of the ball. Since it is proportional to the tangential force, when to the point A the flight distance is 1.0, when to the point B the flight distance will be 0.6.
1.9.2. Momentum of the ball
1.9.2.1. Relation between racket swing and ball flight distance
The momentum is expressed as the product of the ball's mass and velocity.
Momentum = Mass × Velocity
When hitting the ball by a racket, the impulse (the product of the hitting force by the racket and the contact time with the ball) becomes the cause of a flight motion. In dynamics, it is thought that the impulse gives the motion to the object.
Impulse = Force × Contact time
And, the impulse and the momentum are equal.
Mass × Velocity = Force × Contact time
Since the mass of the ball takes a constant value for all balls, the flight speed of the ball increases in proportion to the time when the force is applied, that is, the contact time between the racket and the ball.
1.9.2.2. Angular momentum of the ball
When the ball of radius R is rubbed by a racket, the ball starts to rotate. It is called the moment of force that the product of the R and the friction force in the perpendicular direction to the R.
Moment of force = Radius × Force
Also, the angular velocity (rotation speed) of the ball means the rotation angle per unit time.
Angular velocity = Rotation angle / Time
The momentum of rotation is called angular momentum,
which is expressed by the product that is the ball's inertia moment and the angular velocity, and expresses the momentum of rotation.
The inertia moment is a numerical value that measures the ease of rotation,
and it is determined by the size, shape and mass of a object, and takes the constant value for all table tennis balls.
Angular momentum = Moment of inertia × Angular velocity
And angular momentum equals the product of the moment consisting a force and a contact time.
Angular moment of inertia = Moment of force × Contact time
Angular momentum × Angular velocity = Moment of force × Contact time
This shows that when rubbing with the same force, the angular velocity rises in proportion to longer acceleration time, that is the time length of rubbing with the racket.
1.9.2.3. Momentum of ball rotation and flight
The "Rotational momentum" is more effective than the "Flying momentum" in actual games. It is difficult to estimate the momentum of rotation from the flying ball. If you can hide "the flying momentum of visible" into "the rotation momentum of invisible", you will be able to fool the opponent by the invisible momentum.
Controling the force's magnitude by the racket swing is difficult. Swings require a large acceleration to catch up with the fast ball, which require greater force as a result. Especially, You would feel difficult to swing downing the speed against the fast ball.
However, even when using a large force, you are possible to suppress the amount of the flight momentum if you can raise rotational momentum rate. Yes, if you change the direction of the swing to increase rotational momentum, you would be able to hit a ball with a large momentum. Control the direction of the force, not the magnitude of the force. This can be solved by a problem of consciousness.
So, how do you make a swing of large momentum of rotation that has long contact time with the ball and the racket? Let's look specifically. The swing, which will explain from now, is an important basic technique to support the strategy.
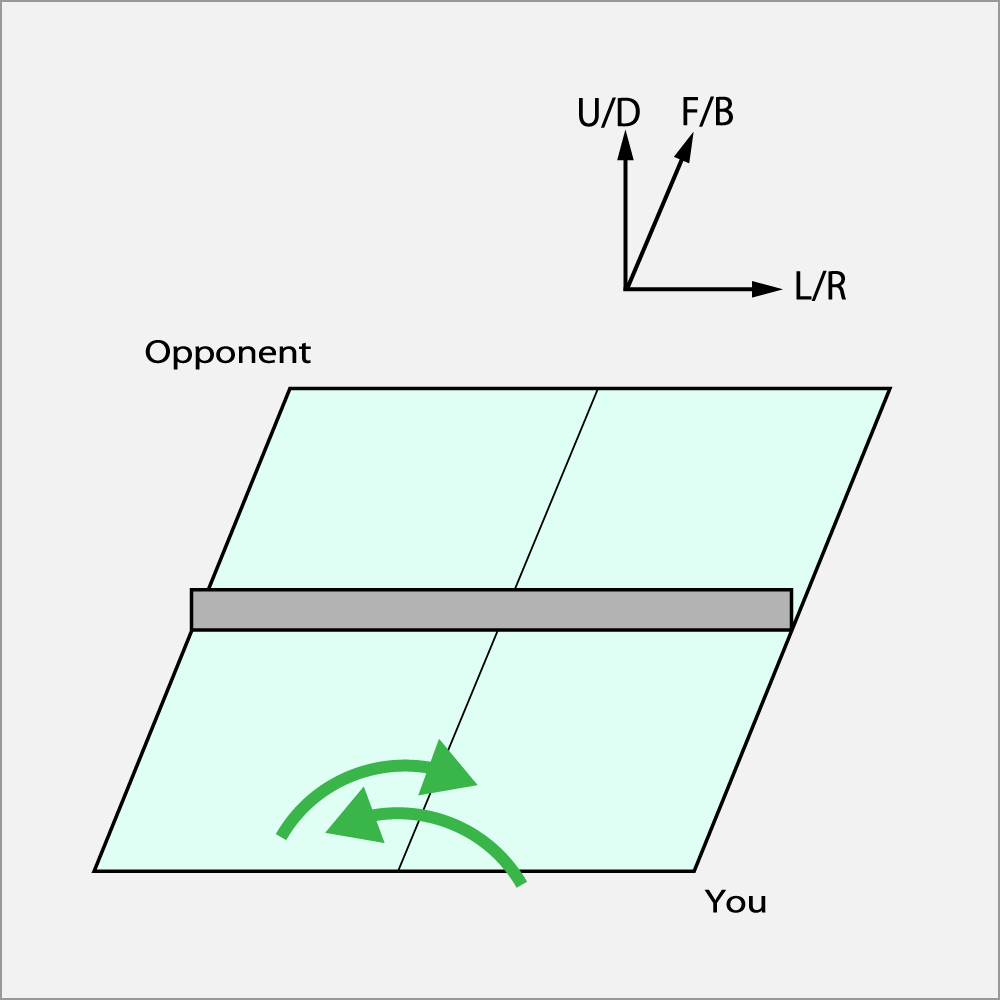
Swing the racket like a wiper
Swing like a wiper. The swing of the wiper suppresses the forward flight distance of the ball and adds a large U/D axis rotation to the ball.
In this example, an example in which the front surface of the ball is rubbed in the left-right direction is shown, but the same effect can be obtained by shaking the ball in parallel with the F/B axis. That is, the forward flight distance is suppressed and a large F/B axis rotation is applied to the ball.