1.9 球と振りの関係
ラケットを振った力が、球へ伝わり、球の飛びと球の回転へと変わる。ラケットの振り半径がラケットの持つ力の主要な因子だ。
ラケットから力を得た球の勢いを表す運動量には、飛びの運動量と回転の運動量がある。
1.9.1 ラケットの振りと飛距離との関係
卓球をしている時には、どうしても球の飛距離をコントロールしたいことがある。サービスでは短い球や長い球を使い分けることが必須となる。また防御や攻撃においても速い球を打つだけではダメで、サイドを狙った短く打つことも要求される。
球へはラケットを介して腕力を伝えるのであるから、腕の振りとラケットの運動量との関係を理解する必要がある。ここではラケットの運動に焦点を当てて述べる。
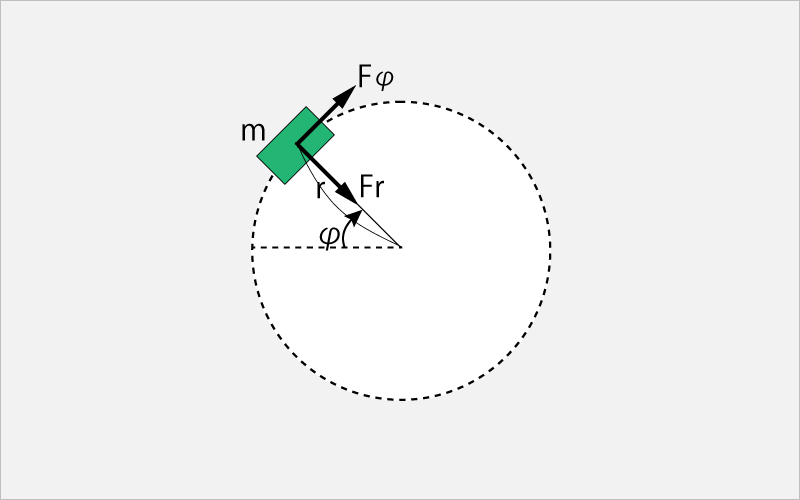
円運動の運動方程式には接線方向の力成分を表す式がある。
次の図で説明すると、質量mの物体が、半径rで、角加速度φ''で運動したとき、物体に加わる力の接線方向成分Fφ、向進方向成分Frとすると、接線方向の運動方程式は以下の通りだ。
mrφ'' = Fφ
即ち、
質量×回転半径×物体の角加速度 = 接線方向の力成分
Fig-1.9.1a
これをラケットの振りへ適用すると、
ラケットの質量 × 振りの半径 × 振りの角加速度 = 接線方向の力成分
円運動の運動方程式では、接線方向の力成分Fφは、ラケットの振り抜き半径と比例関係にあること示している。
ラケットの振りで力成分を制御するには、ラケットの振り抜き半径で調整する方が振りの角加速度で調整するより遥かに易しい。
この場合の振りの半径とはX-Y平面すなわち卓球台に投影した半径を指している。
振り抜き半径は、ラケットあるいは肘を立てることでも出来る。もう一つの方法は手首と腕関節の中間点を中心として回転させて行うこともできる。
なお、向力方向に力成分Frについては、ここでは腕を回転すると自然にかかってくるので考える必要がない。
<具体例>
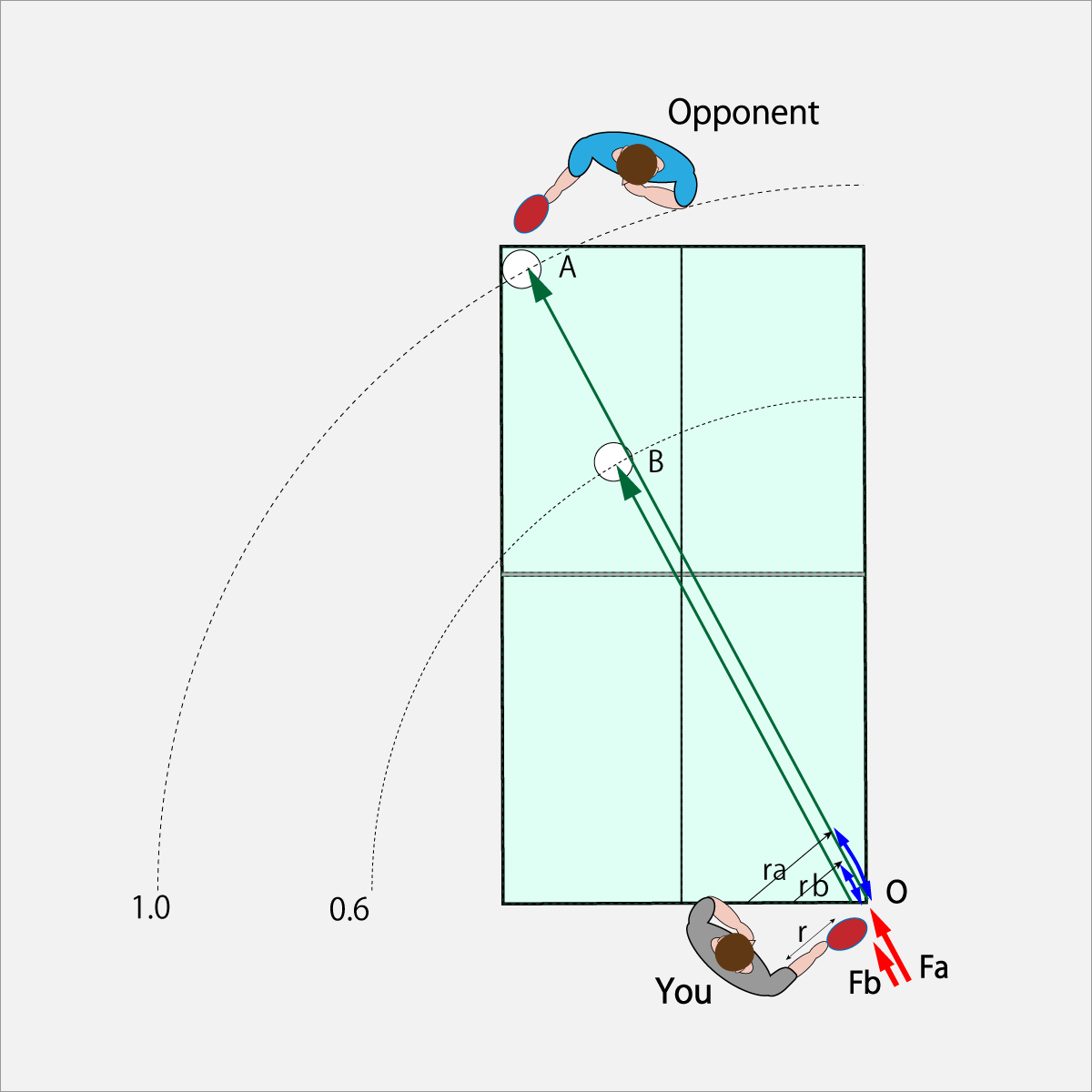
次の図を見てほしい。この図はサービスをイメージしている。だから相手からの球の影響はないものとしている。
球の飛行方向はAとBとで同一方向である。また、AとBとではラケットの回転角速度は同一速度で振り抜いている。
しかしながら、ラケットのスイング半径は、A点の場合は ra=1.0とした時、B点の場合は rb=0.6としている。
したがって、接線方向の力Fの大きさは、スイング半径に比例するので、Aでの力を Fa=1.0とした時、Bでの力は Fb=0.6となる。
そして、球の飛距離は、接線方向の力に比例するので、Aの飛距離は1.0とした時、B点の飛距離は0.6となるのだ。
Fig-1.9.1b
1.9.2 球の運動量
ここでは、ラケットによって加えられた力がボールの運動とどう結び付くか、ボールの運動に焦点を当てて述べる。
1.9.2.1 球の飛びの運動量
球の速度と球の質量の積を運動量という。
運動量 = 球の質量 × 速度
ラケットで球を打つと、球にはラケットから受ける力と接触している時間の積の力積が、 球の飛びの運動の原因となる。物理では、力積が物に運動を与えると考えている。
力積 = 力 × 時間
そして力積とボールの運動量は等しい。
球の質量 × 速度 = 力 × 時間
球の質量は全ての球で一定の値をとるから、球の飛行速度は、力を付加している時間、 すなわちラケットと球の接触時間に比例して速くなるのだ。
1.9.2.2 球の回転の運動量
球の回転の運動量を角運動量という。半径Rの球をラケットで擦ると球は回転を始める。Rとの直角方向の擦る力成分とRとの積を力のモーメントと言う。
力のモーメント = 半径 × 力
また、球の角速度(回転速度)は、単位時間当たりの回転角度を言う。
角速度 = 回転角度 / 時間
回転の運動量のことを角運動量と言い、球の慣性モーメントと角速度の積で表され回転の勢いを表している。 慣性モーメントは回転のし易さを図る数値であり物の大きさと形状と質量で決まり、全ての卓球の球は一定の値をとる。
角運動量 = 慣性モーメント × 角速度
そして角運動量は、力のモーメントと接触時間の積とに等しい。
角運動量 = 力のモーメント × 接触時間
慣性モーメント × 角速度 = 力のモーメント × 接触時間
これは、同じ力で擦る時、加速時間が長ければ、すなわちラケットで擦る時間に比例して角速度が上がることを示している。
1.9.2.3 球の回転と飛びの運動量
「飛びの運動量」より「回転の運動量」は実戦ではより効果的だ。
飛んでいる回転の運動量は見ることは難しい。見える「飛び」の内に、
見えない「回転の運動量」をコントロールできれば相手は見えない運動量に翻弄されることになる。
予定の飛距離を得るのに、予定の腕の回転半径を小さくすることが出来ない場合は、 力の大小をコントロールするのは難しくなる為に。結果として、球へ大きな力を加えることになりコートから出てしまう。
しかし、大きな力を使うにしても、 その力を回転の運動量に多く使えば、飛びの運動量は小さく抑えることが出来る。これは、意識の問題で解決することが出来るのだ。
それでは、どうしたら、球との接触時間の大きい「回転の運動量」を多く与えるスウングが出来るのだろうか。 具体的に見ていこう。これから述べる振りは、戦略を支える重要な基礎技術となるだから。
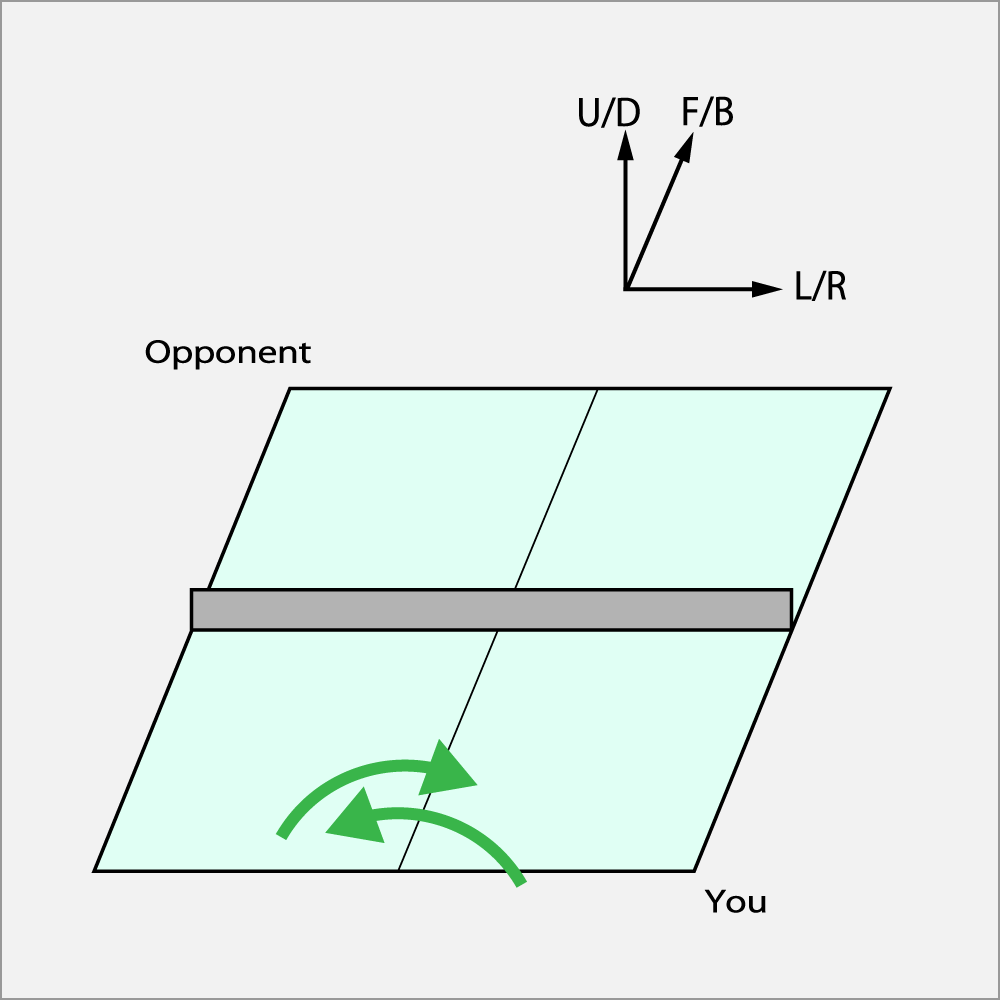
U/D軸あるいはF/B軸に平行に振る。
ワイパーの様に振る。ワイパーの振りは球の前方引飛距離を抑え、球へ大きなU/D軸の回転を加えることになる。
下の図ではボールの正面を左右方向に擦る例を示したが、F/B軸平行に振っても、同様の効果が得られる。即ち、前方の飛距離を抑え、球へ大きなF/B軸の回転を加えることになる。
Opponentは対戦相手側のことであり、Youは自軍側を指している。
Fig-1.9.2