1.12. The Angular Momentum at Impact Point

In this section we are going to learn "a New Spin Consisting a Racket Swing and the Spin" that is the core of this book. Any spin can be composed. You can create a new spin from the rotation of the ball and swing, so you are able to control the ball exactly as you want.
Here, before considering the application of rotation described in the next chapter, let's consider a little more about the ball's rotational speed and the dynamical implications of the hitting point.

Actually, the rotation composition points to the composition of angular momentum which means the vigor of rotation.

Angular momentum ＝ Mass　×　(Radius of ball)²　×　Angular velocity

You can see the angular momentum. It is the momentum of flying when you hit the rotating ball against the stopping racket. And that is largest on the ball's equator. Because it relates to the square of ball radius, it becomes rapidly smaller toward the poles and it is zero at the poles.

When the spinning ball hits into the stopped racket, the ball receives a angular momentum in the opposite direction by the rubber reaction, however the angular momentum decreases toward the pole from the equator line.
The spin stops if you hit the spinning ball on the equator line. But the spin is keeping if you hit it near the poles.

In the below figure "Tangential velocity and Angular momentum", Sin indicates the tangential velocity respect to angle θ.
Sin² indicates the ratio of the angular momentum perpendicular to the rotation axis at angle θ.

Now we suppose that the total angular momentum which is given at the ball's equato is 100%.
If the ball hits the rubber at angles 90 °, 100% of the total is consumed to flying.
However,
If the ball hits the rubber at angles 45 °, 50% of the total is consumed to flying, the other 50% remains as rotation.
If the ball hits the rubber at angles 30 °, 25% of the total is consumed to flying, the other 75% remains as rotation.
If the ball hits the rubber at angles 20 °, 12% of the total is consumed to flying, the other 88% remains as rotation.

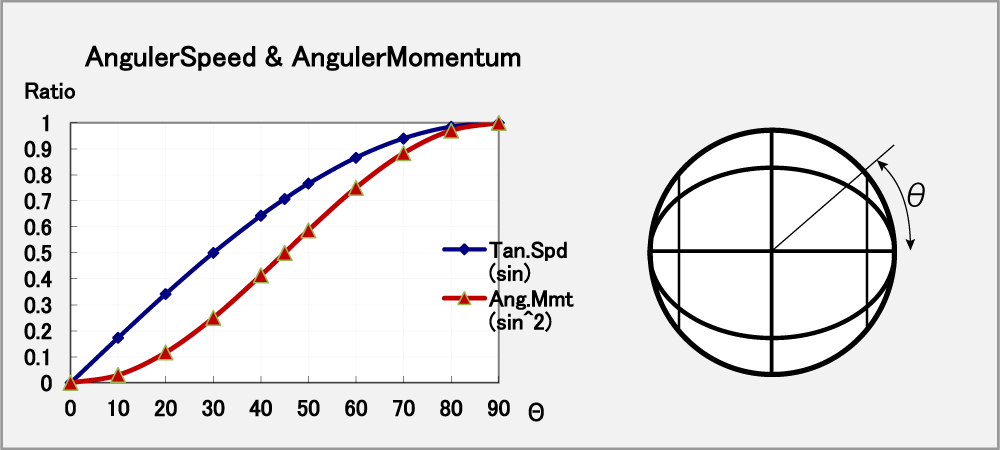
Reference: Angular momentum remaining in the ball when touched at the contact angle Θ

In accordance with Section 1.11, the above is described by the equation as follows.
Iω’(t) = N

I : the moment of inertia, ω : the angular velocity, ω₀ : the initial angular velocity, r: radious, N :torque

When it integrated with time,
Iω(t) = N(t - t₀) + Iω₀
= r F(t - t₀) + Iω₀

When the ball contacts with the rubber at an angle Θ, the force F stops the spin due to rubber reaction force, and changes to flying.
Iω(t) = r m (v(t) – v₀ ) + Iω₀
Angular momentum at the angle Θ
Iω_Θ(t) = r sinΘ m (v(t) –v₀ ) + Iω₀

The spin stops rotation, then it substitutes v (t) = 0
Iω_Θ(t) = - r sinΘ m v₀ + Iω₀

Since the tangential velocity at the angle v₀ = r sinΘ ω₀, I = mr²,
Iω_Θ(t) = - m (r sinΘ)² ω₀ + mr²ω₀
= m r²ω₀ - m (r sinΘ)²ω₀
= m r² (1 - sin²Θ)ω₀

Return