1.12 打球点の角運動量
次章では、「球と振りの回転の合成」を学ぶ。回転は合成出来るので、
球と振りの回転を合成出来れば、自分の思う様に球をコントロール出来るのだ。
ここでは、次章で説明する回転の応用を考える上で、もう少し、球の速度とか、球の打球点の力学的意味合いを考える。
実は回転の合成とは、角運動量の合成を指している。球の角運動量とは、回転の勢いを言う。
角運動量 = 質量 × (球の半径)2 × 角速度
角運動量は、見ることが出来る。回転している球を停止しているラケットにあてた時の飛びの勢いだ。 球の半径の二乗に関係しているから、球の赤道線では大きく、極に向かうに従って急速に小さくなり、極では零となる。
回転がラケットに当たると反作用により回転の方向と逆に角運動量を受けるが、赤道線上から極に向かうに従って小さくなる。
球の赤道線上でラケットに当たると、球は回転を止めるが、極の近くに当たった球では回転を止めない。
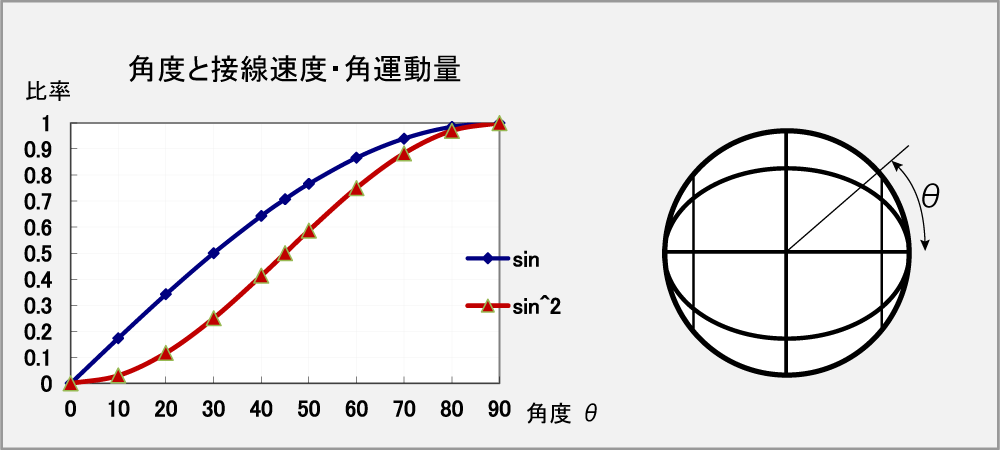
下の図「角度と接線速度・角運動量」では、sinは角度θに対する接線速度、
sin2は角度θでの回転軸に直角な角運動量の比を示す。
球の赤道で与えた回転軸に対する角運動量を1とすると、球が角度90°でラバーに当たれば角運動量は全て消費されるが、
球が角度45°でラバーに当たれば、0.50の角運動量が飛びに変換し消費し、0.50が回転として残る。
球が角度30°でラバーに当たれば、0.25の角運動量が飛びに変換し消費し、0.75が回転として残る。
球が角度20°でラバーに当たれば、0.12の角運動量が飛びに変換し消費し、0.88が回転として残る。
Fig-1.12.1
<参考>接触角度Θで触れた時の球に残る角運動量
上記について、1.11節に倣って方程式で説明すると以下のとおりとなる。
Iω’(t) = N
I:慣性モーメント、ω:角速度、ω0:初期角速度、 r: 球の半径、N:トルク
tで積分すると、
Iω(t) = N(t-t0) + Iω0
= r F(t-t0) + Iω0
角度Θでラバーに接触すると、力Fは、球はラバー反力で、回転を停止して飛びに変わるので、
Iω(t) = r m (v(t) –v0 ) + Iω0
角度Θでの角運動量は、
IωΘ(t) = r sinΘ m (v(t) –v0 ) + Iω0
回転は停止するので、v(t) = 0を代入すると
IωΘ(t) = - r sinΘ m v0 + Iω0
角度Θでの接線速度は、
v0 = r sinΘ ω0、I = mr2 なので、
IωΘ(t) = - m (r sinΘ)2 ω0 + mr2ω0
= m r2ω0 - m (r sinΘ)2ω0
= m r2 (1 - sin2Θ)ω0