1.11. Relational Expression between Ball and Swing Speed
Regarding the contents of the section 1.16 "Spin Speed and Swing Speed", this section is expressed somewhat strictly with the angular motion equation.
Although differential equation comes out, each case is explained, so you will be able to understand it seening combined with the figure.
Let's expand the Newton's fist law of motion to rotational motion.
When the rotation is changed, a force moment is acting on it. If the moment is not acting, the current rotation is continued, or if there is no rotation, it continues non rotation.
The defferential equation expresses this meaning.
Coordinate & Restraint Condition
- The rotation handled here is one-dimensional coordinates.
- The friction of the rackets' rubber is sufficiently large and shall be no slippy.
- The mass on the racket side is sufficiently larger than the ball, and the racket cannot be moved by the ball.
Ball Angular Momentum Equation
The angular momentum equation of the table tennis ball is
I ω'(t) = N
When integrated with time,
I ω(t) = N (t - t0) + I ω0
Here
I : the moment of inertia, ω : the angular velocity, ω0 : the initial angular velocity, N : the moment of applied force, t : the reference time, R : the angular momentum due to the reaction force, v0 : the initial rotational speed, v : the rotational speed, r : radius, m : mass
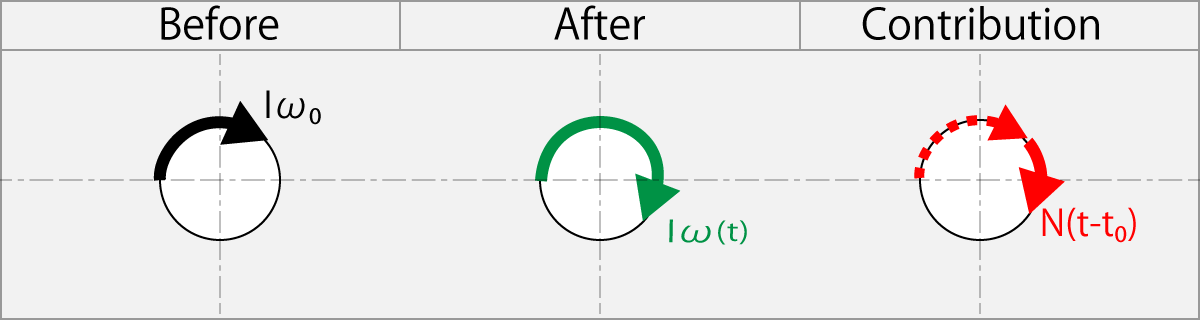
1.11.1. Rubbing Forward with ω(t) Faster than The Initial Rotation ω0
Rubbing condition
ω(t) > ω0
The added angular momentum
N(t - t0) = Iω(t) – Iω0
This formula is used when the ball is rubbed for the forward rotation direction by racket with an angular velocity ω (t) faster than the initial angular velocity ω0.
the torque N (t - t0) worked to increase the rotation speed from ω0 to ω(t).
The following figure shows the relationship of it; the initial angular momentum to the left side,
the result one to the center, and the contributed one to the right side.
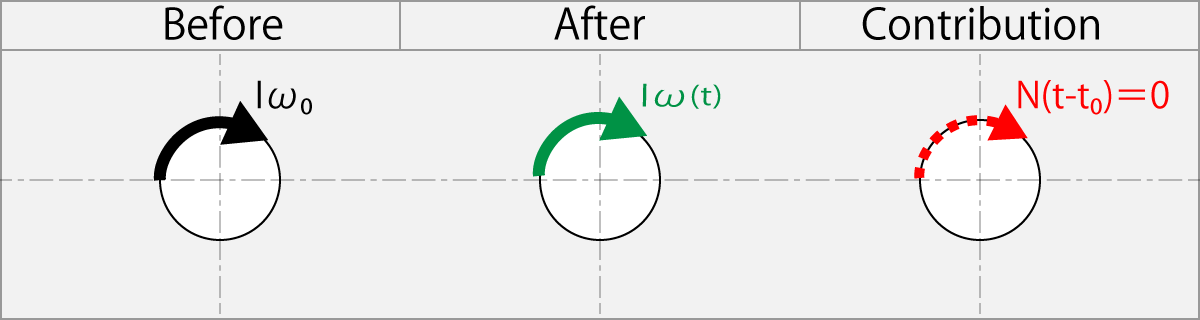
1.11.2. Rubbing Forward with ω(t) as The Same Speed as The ω0
Rubbing condition
ω(t) = ω0
The added angular momentum
N(t - t0) = Iω(t) – Iω0
=0
This equation shows that torque N (t - t0) does not contribute when the ball is rubbed in the forward rotation direction by racket having an angular velocity ω (t) equal to the initial angular velocity ω0 of the ball.
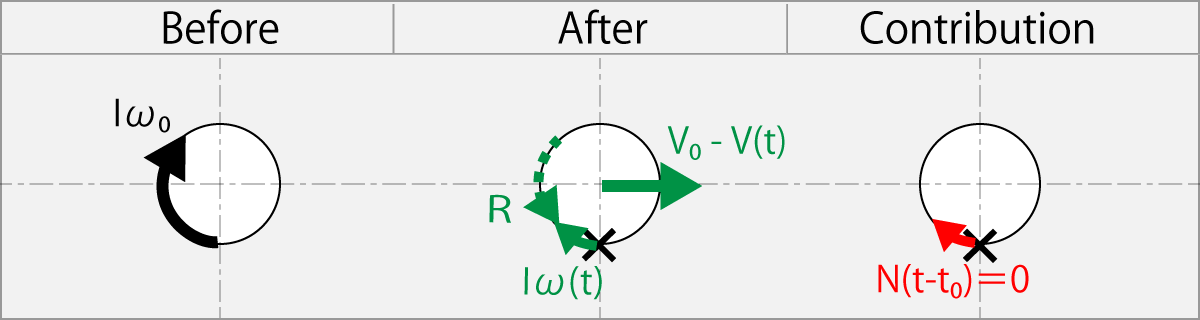
1.11.3. Rubbing Forward with ω(t) Lower than The ω0
Rubbing condition
|-ω(t)| > ω0
Conversion to flight speed by friction with rubber
R = Iω(t) – Iω0
m(v0 - v(t))r = Iω(t) - Iω0
This equation shows when you rubbed for the forward rotation direction by racket with angular velocity ω(t) lower than the initial velocity ω0 of the ball. If the rubber is slippy, the difference ω0 - ω(t) is remained on the ball.
But, if the rubber is non slippy, the brake is applied in the opposite direction to ω0. Since the axis of the ball is not fixed the ball cannot rotate the racket, so the difference of the angular momentum of rotation changes to the ball’ s flight speed v0 – v(t) due to the inertial force.
The actual rubber is in between.
The X in the figure indicates the place to rub a ball with the racket.
When the rubber is non slippery
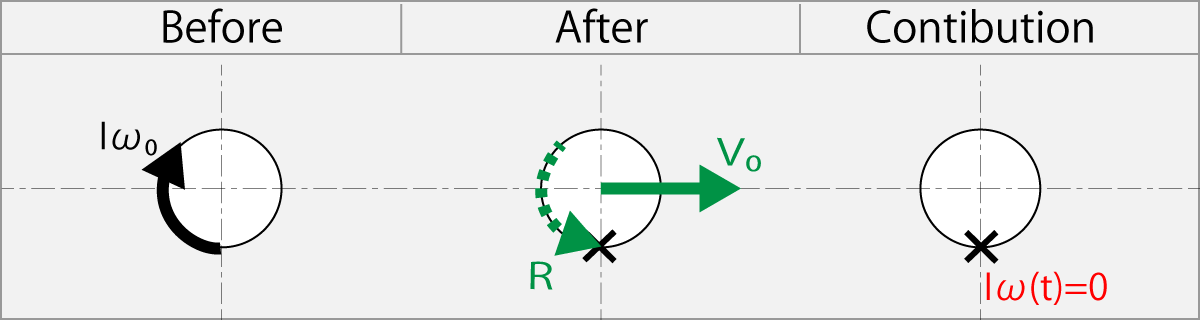
1.11.4. Hitting The Ball of The ω0 by The Racket of Zero Rotation
Rubbing condition
ω(t) = 0
Conversion to Flight speed by the friction from the rubber
R = Iω(t) – Iω0
R = 0 – Iω0
m v0 r = - Iω0
This equation shows when the racket hits the ball without giving a rotation.
Since the axis of the ball is not fixed since the ball cannot rotate the racket, then the angular momentum of rotation changes to the flight of the ball due to the inertial force.
The X in the figure indicates the place to rub the ball with a racket.
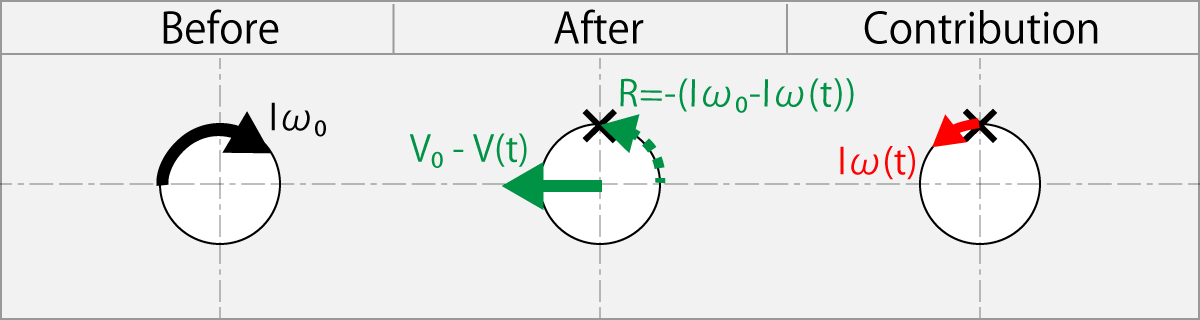
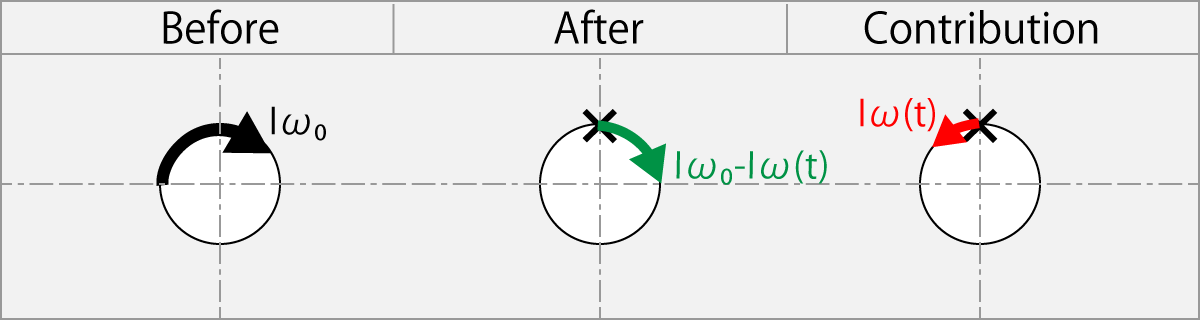
1.11.5. Rubbing Reverse with ω(t) Lower than The ω0
Rubbing condition
|-ω(t)| < ω0
Conversion to Flight speed by the friction from the rubber
Iω(t) = R + Iω0
R = - (Iω0 - Iω(t))
m(v(t) – v0)r = - (Iω0 - Iω(t))
This equation shows the case where the ball is rubbed in the reverse rotation direction by racket having an angular velocity ω (t) slower than the initial angular velocity ω0. If the rubber slips, the difference in angular momentum Iω0-Iω (t) remains on the ball.
But if the rubber has no slip, since the axis of the ball is not fixed the ball cannot rotate the racket, so the difference of the angular momentum of rotation changes to the ball’s flight speed v(t) – v0 due to the inertial force.
The actual rubber is in between.
The X in the figure indicates the place to rub a ball with the racket.
When the rubber is non slippery
When the rubber is slippery
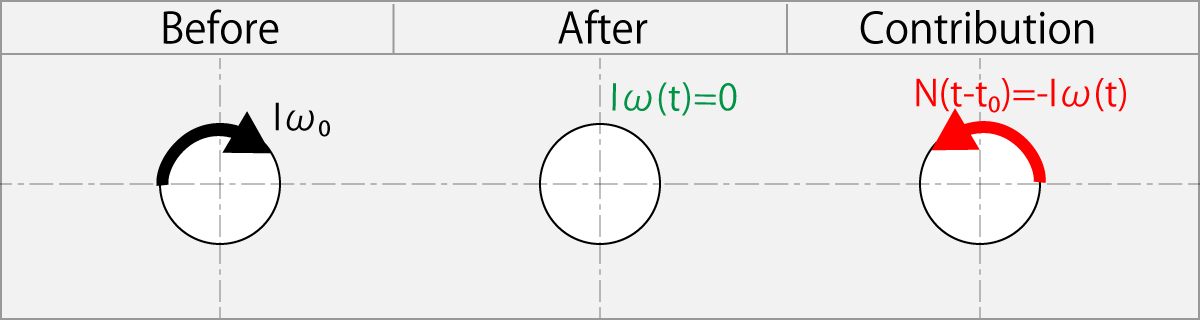
1.11.6. Rubbing Reverse with ω(t) as The Same Speed as the ω0
Rubbing condition
N(t - t0) = - ω0
The result angular momentum
Iω(t) = N(t - t0) + Iω0
Iω(t) = – Iω0 + Iω0
Iω(t) = 0
This equation indicates that the ball stops rotating when rubbed in the reverse rotation direction by racket having an angular velocity ω0 equivalent to the initial angular velocity ω0 of the ball.
1.11.7. Rubbing Reverse with ω(t) Two Times Higher than The ω0
Rubbing condition
N(t - t0) = - 2ω0
The result angular momentum
Iω(t) = N(t - t0) + Iω0
Iω(t) = – 2 Iω0 + Iω0
Iω(t) = – Iω0
This equation shows that when the ball is rubbed for the reverse rotation direction by racket having an angular velocity of 2ω0, which is twice the initial angular velocity of the ball, the ball starts rotating in the reverse direction to ω0.
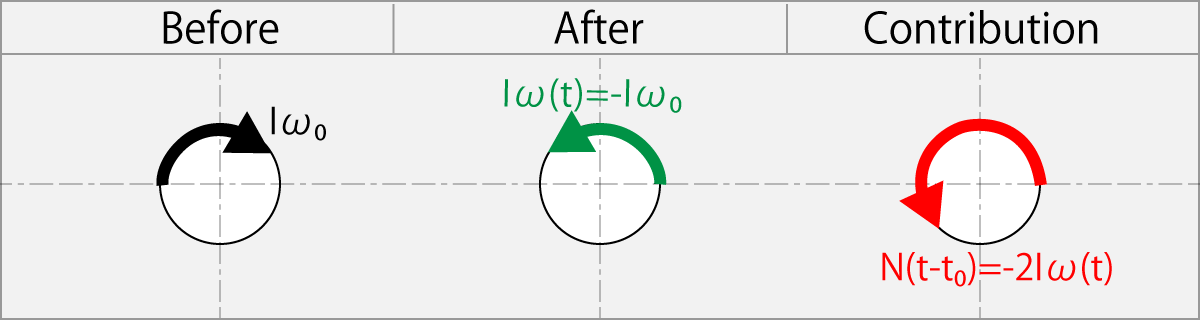
Since N t = F r t, for to double N t, F can be doubled and also t can be doubled, that is the contact time can be doubled.
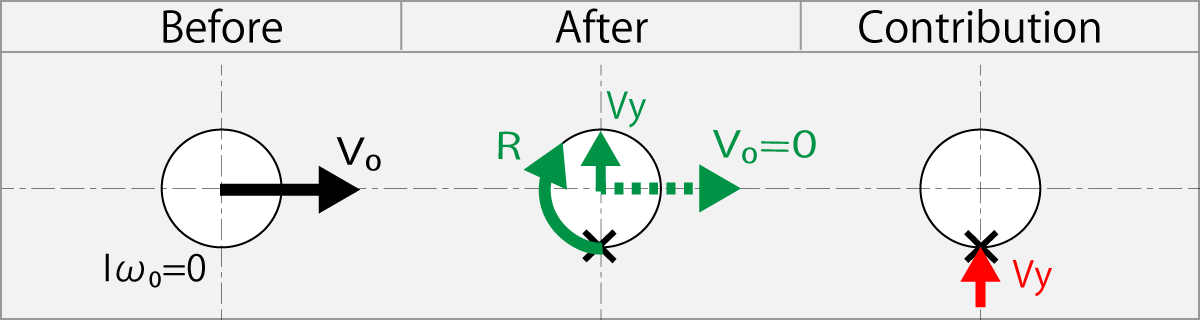
1.11.8. Hitting The Ball Perpendiculary with The Racket without Giving Rotation
Rubbing condition
ω(t) = 0
Conversion to angular momentum by flight stopping
m(v0 - v(t)) r = I ω(t) - I ω0
m(v0 - 0) r = I ω(t) - 0
Iω(t) = m v0 r
This formula shows that a racket with rubber which has a large friction coefficient hits a flying ball at any speed Vy on the perpendicular direction.
By moving the racket in the direction perpendicular for the ball's flight direction and making contact with it, the ball stops flying by resistance on the racket surface, but since the axis of the ball is not fixed, when the ball leaves from the racket, the flight turns into rotation. In this figure, it is assumed that the racket hits perpendicular to the ball at the point X.
1.11.9 Important Difference between Rubbing of Forward and Reverse Rotation
The difference between rubbing of forward rotation and reverse rotation is not limited to the above. There are important differences. In reverse rotation, the energy exchange between the ball and racket is performed instantaneously. But rubbing in a forward rotation, the exchange becomes long, so the contact time between the ball and the racket is long, as shown in Section 1.9.1 Ball jump and momentum. It has a noticeable effect of flying distance of the ball. This is important, you need to remember it when considering the tactics of table tennis.