Part 2. Think Tactics acoording to Vectors
2.1. Spin Composition from a Racket Swing and Ball Spin
Even if you strike a spining ball to your intended direction, the ball always deviates from the direction. You cannot fly into the direction. In order to rotate the ball into the intended spin direction and to fly the ball into the intended one, you have to add the spin determined by dynamic theory to the ball with the racket.
Spin is vector, and each spins can be combined.
When combining spins, the spin vectors that is the direction of spin axis must be determined. There are promises to it. The direction of a spin is the advancing direction of a right screw, and the length of a vector is the spin strength. We need to confirm how to take coordinates before seeing a concrete example.
2.1.1. How to take the spin axis
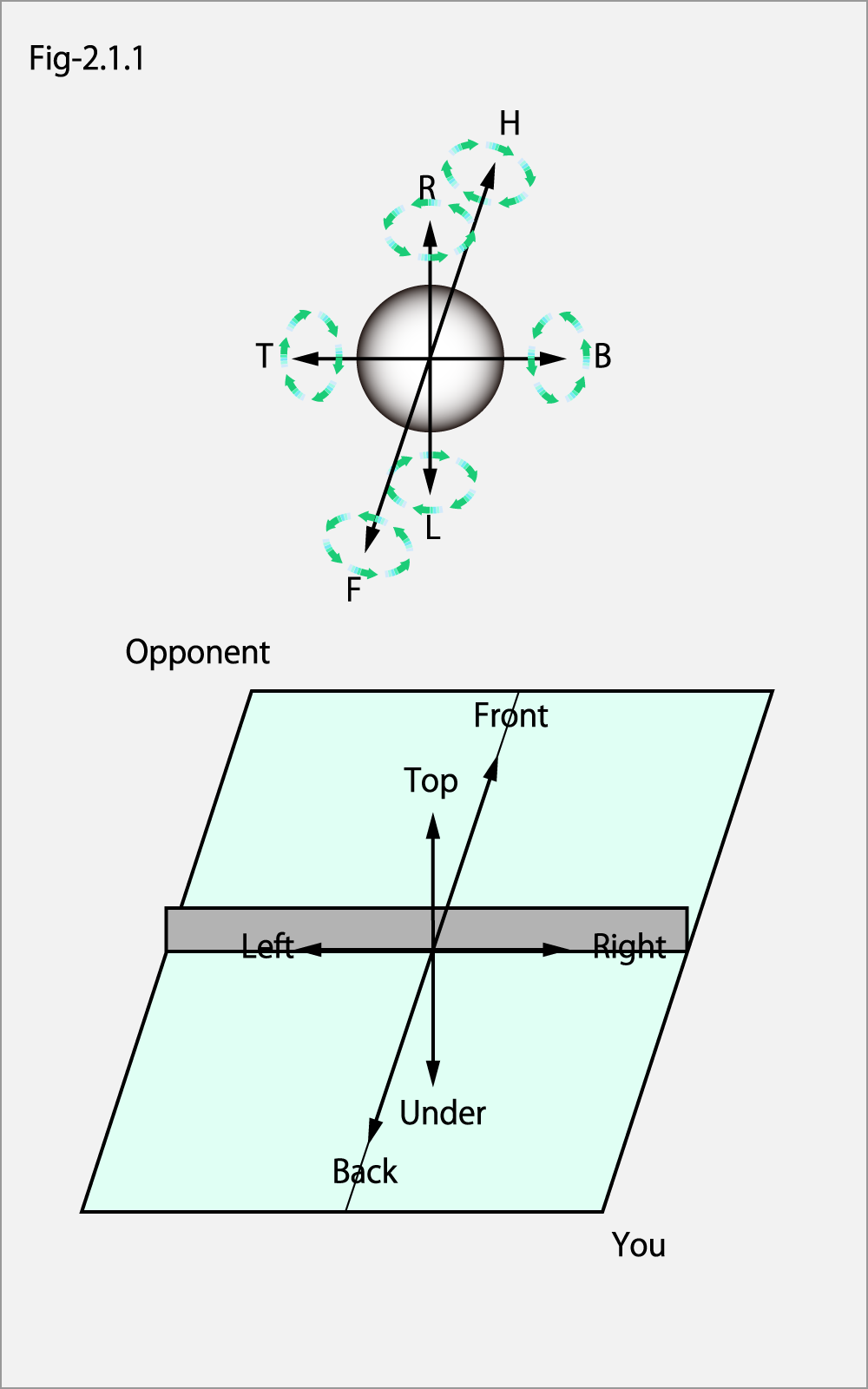
Order to make a spin familiar, we will name the spins. From now on, the spins will be talked by the rotation seen from your side.
First, let's match the coordinate axis of the table tennis table with the spin axis of a ball.
The below figure shows the coordinates of the table tennis table. In this figure supposes that you are on this side and the opponent is across the table. the derection of facing the opponent is called as Front-Back axis, the derection spreading both arms is called as Left-Right axis, and the derection upper and lower the table is called as Top-Under axis.
The upper figure shows the spin axis.
The front axis indicates clockwise rotation (also referred to as H cork or H). H is the initial letter of Head cork spin representing clockwise rotation in English.
The back axis indicates counterclockwise rotation (also called F cork or F). F is the initial letter of Foot cork spin representing counterclockwise rotation in English.
The right axis indicates downward rotation (also called Cut or B). It is a rotation that rubs the ball's lower hemisphere forward. B is the initial letter of Back spin representing downward rotation in English.
The left axis indicates upward rotation (also referred to as Drive or T). It is a rotation that rubs the ball's upper hemisphere forward. T is the initial letter of Top spin representing upward rotation in English.
The upper axis indicates right rotation (also referred to as Curve or R). It is a rotation that rubs the ball's right side forward. R is the initial letter of Right-side spin representing rightward rotation in English.
The lower axis indicates left rotation (also called Shoot or L). It is a rotation that rubs the ball's left side forward. L is the initial letter of Left-side spin representing leftward rotation in English.
The above spin names were adopted in order to prevent overlapping each other.
<Spin Composition>
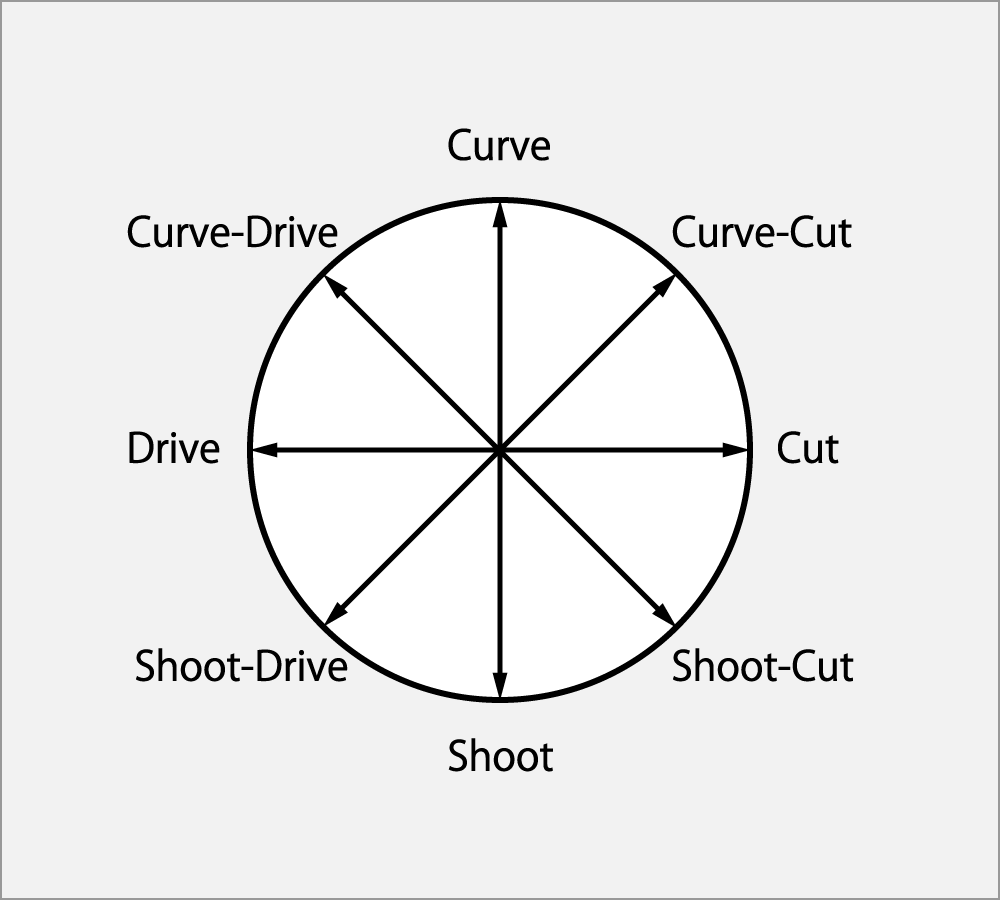
Furthermore, the spin composed of Curve and Cut is called Curve⋅Cut,
and the one composed of Shoot and Cut is called Shoot⋅Cut.
And the spin composed of two or more spins can be expressed in the same way.
The left figure shows the spin names that composed from the spins of the Curve / Shoot axis and Cut / Drive axis.
Note)
The Curve-Drive and the Drive-Curve is the same spin.
But, on this site is provided with the naming principle for combining two or more spins.
it takes the order of Clock / Cclock axis, Curve / Shoot axis and Drive/ Cut axis.
Of course if there is no applicable spin, its name is omitted.
The Θ shall be put before the spin when you view a spin from the standpoint of your opponent. (Let's call it "Theta from the opponent's point of view" or just "Theta")
The Θ is used as a minus meaning on this book.
Because, the minus of (-) uses 3 characters but using the Θ can be dealt with in a single character.
The Drive which the opponent provides is called ΘDrive, the spin is translated to Cut when you view the spin from your own side.
Therefore, it converts the rotation from the opponent spin to your spin as follow.
ΘDrive = Cut (ΘT = B). Similarly,
ΘCut = Drive (ΘB = T)
ΘHcork = Fcork (ΘH = F)
ΘFcork = Hcork (ΘF = H)
For horizontal spin, the rotation of opponent's spin and your spin is the same.
ΘCurve = Curve (ΘR = R)
ΘShoot = Shoot (ΘL = L)
Let us write some examples of the composition of the horizontal and vertical spin.
ΘCurve⋅Cut = Curve⋅Drive (ΘRB = RT)
ΘHcork⋅Cut = Cclock⋅Drive (ΘHB = FT)
ΘShoot⋅Drive = Shoot⋅Cut (ΘLT = FB)
ΘFcork⋅Drive = Hcork⋅Cut (ΘHT = FB)
Clearly, if you can predict the spin kind which the opponent provides, the Θ can be allow to omit, for example, in the case of Curve or Shoot where the rotation does not change at opponent's standing position.
Since the spin composition is the addition of spin and spin, in the case of expressed formally as a vector, the simbol of additon will be "+", but on this site, it is expressed as "⋅". For example the spin vector obtained by combining Curve and Drive is Curve + Drive in formally, but it is expressed as Curve⋅Drive.
And also, when it is expressed in English initials, that "·" is also omitted. In this example, the composite vector of the curve (R) and the drive (T) is R + T but it is expressed as RT.
2.1.2. Tactics diagram of vector
Let's take a quick example.
There are several promises to view this figure.
- The arrow from the ball is the spin vector seen from your side.
- The black vector is the spin coming from "opponent → you", and the result that added the red vector to the green one. A thin black broken line indicates the spin path.
- The red vector is "The spin imparted with the racket" by you or your opponent swing. The first shot starts in red, but it can be omitted to avoid complexity.
- The green vector is the spin that goes to “you → your opponent”, the result of adding the black vector to the red one. A thin green broken line indicates the route.
- Each number in the circles indicates the order of ball hitting.
- Each number in the square boxes indicates the order of a trajectory.
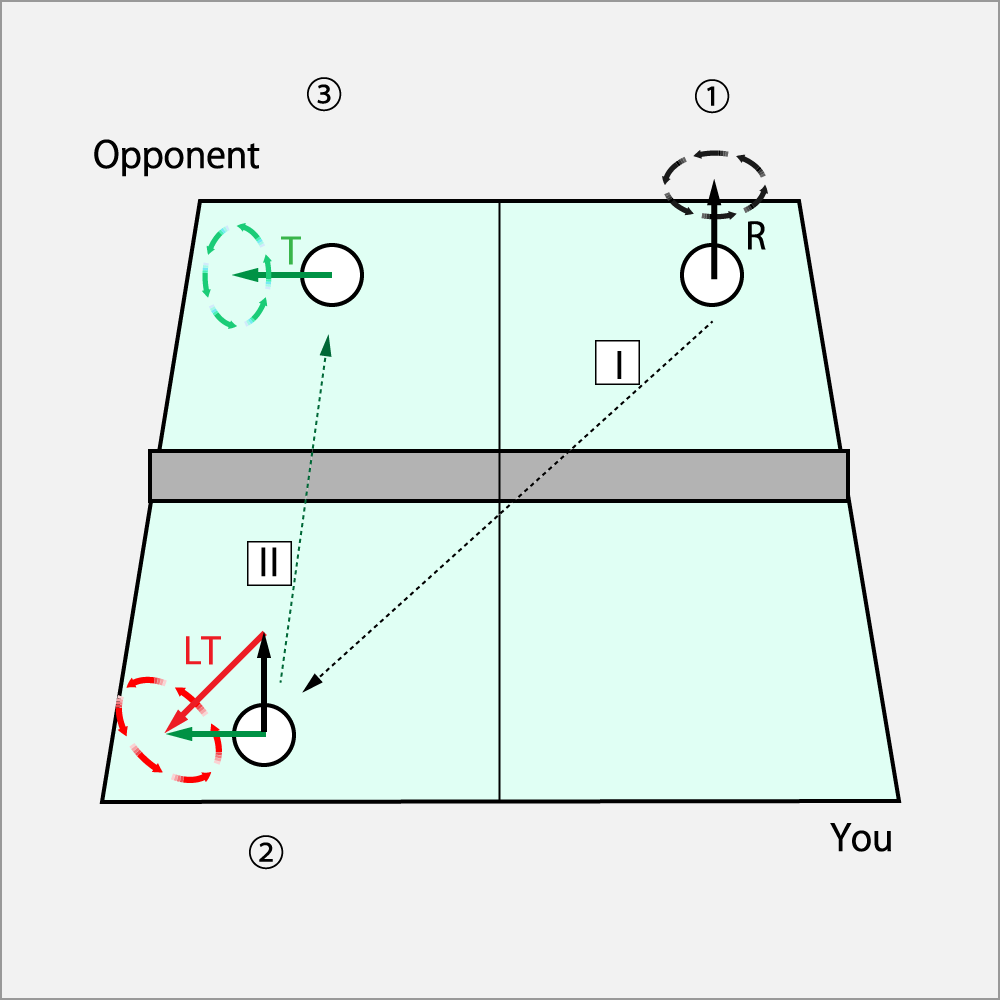
Let's look at the order of ball hitting.
① The opponent has made a service by Curve (R) to your racket backside.
② You add Shoot⋅Drive (LT) to the spin on the trajectory-1 entered your coat.
③ The ball will be returned as Drive (T) on the trajectory-2 to the opponent's coat.
Equation is as follows.
Drive = Curve + Shoot⋅Drive
When expressed in English initials,
T = R + (L+T)
as R = - L,
then T = T
<Vector diagram>
Arrows in the vector diagram indicate the direction of a right screw.
The black is a spin vector from your opponent.
The red is your additional one.
The green is a target one which added the red to the black.
The vector ② that you want to add needs to connect from the end-point of the opponent vector ① to the end-point of the target vector ③.
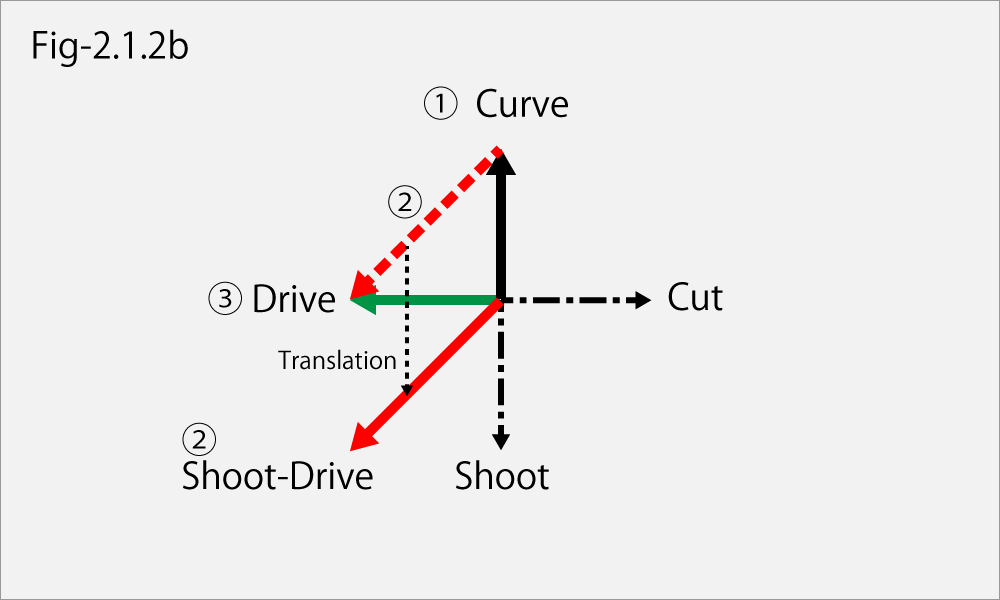
There is a caution.
When you need a vector which connects a Curve to the Drive, you should not just regard it is a composite vector as Curve⋅Drive.
Its name is wrong.
Naming of vector should be based on the origin point.
So in this case, the dot-red-line of connecting the Curve and Drive has to be translation to the origin.
Therefore, this vector becomes a Shoot⋅Drive.
2.1.3. The tool for thinking about rotation

It is hard to think about the spin composite of three-dimensional only in our head and will make mistakes often.
So, I bought a divider for drafting and made a tool by removing needles.
If you would also make it, you will become to develop new strategies on desk easily since you can be considered in advance the rotation that you add to the opponent's spin.
When it applied to the above vector diagram, when the upward vector ← IN is the Curve and the left vector ← OUT is the Drive , the vector connecting IN to OUT becomes the Shoot⋅Drive of rotation vector added. Also, when the rotation to return the ball is Drive, the direction of the OUT vector is always to the left.
Now, let's move on to Advanced Guide.
Since the spin from your opponent can predict from their hitting swings or receiving ones,
I prepared optimum spins corresponding it. Those are the proved options I usualy use.