2.1 球と振りの回転の合成
回転している球に、方向を定めて打っても、球は、その方向と必ずずれてしまう。 意図した方向に飛んでいかない。意図した方向に回転させ、 また、意図した方向に球を打つためには、ラケットでベクトルから定まる回転を球へ加えることによって行う。
回転はベクトルであり、回転同士を合成できるのだ。
回転を合成する時は回転軸の方向と回転方向を決めてやらねばならない。
これには約束がある。回転は右ねじの進む方向を回転のベクトルの方向とし、
その長さをベクトルの大きさ、すなわち、回転の強さとする。
具体例を見る前に座標の取り方を確認しておきたい。
2.1.1 回転軸の取り方
回転を身近なものとする為に、回転に名前を付けることにする。回転は自分から見た回転で話をする。
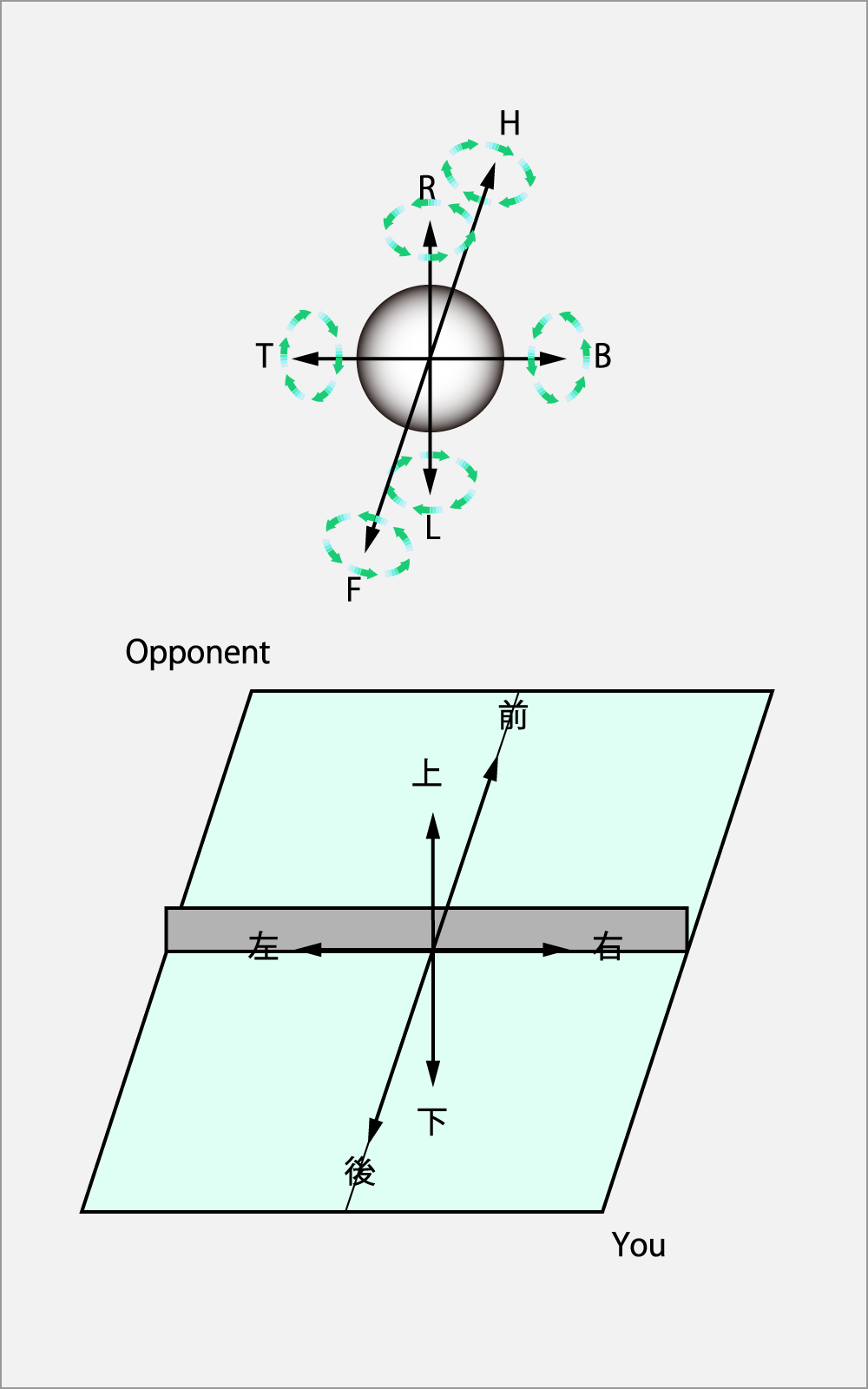
最初に卓球台座標軸とスピン座標軸を合わしておこう。
下図は卓球台の座標を示している。こちら側に自分(You)がいて、卓球台を挟んで対戦相手(Opponent)が居るものとしている。
相手との対面軸を前後軸とし、両手側を左右軸とし、上下を上下軸としている。
上図は球のスピン座標軸を示している。
前軸は時計回転(HコークあるいはHとも呼ぶ)を示している。
Hは英語で時計回転を表すヘッドコークスピンの頭文字を取っている。
後軸は反時計回転(FコークあるいはFとも呼ぶ)を示している。
Fは英語で反時計回転を表すフットコークスピンの頭文字を取っている。
右軸は下回転(カットあるにはBとも呼ぶ)を示している。球の下半球を前方に擦る回転だ。
Bは英語の下回転を表すバックスピンの頭文字を取っている。
左軸は上回転(ドライブあるいはTとも呼ぶ)を示している。球の上半球を前方に擦る回転だ。
Tは英語の上回転を表すトップスピンの頭文字を取っている。
上軸は右回転(カーブあるいはRとも呼ぶ)を示している。球の右側を前方に擦る回転だ。
Rは英語で右回転を表すライトサイドスピンの頭文字を取っている。
下軸は左回転(シュートあるいはLとも呼ぶ)を示している。球の左側を前方に擦る回転だ。
Lは英語で左回転を表すレフトサイドスピンの頭文字を取っている。
※英語では前後軸の回転をコークと呼ぶが、前後の回転を区別していない。そこで、ここでは前方を表すH(ヘッド)、その反対側をF(フット)で表した。
同様に、上下軸の回転をサイドスピンと呼ぶが、上下の回転を区別していないので、ここでは、右方を表すR(ライト)、その左方をL(レフト)で表した。
また、
スピンの頭文字はお互いに重ならないようにするために、上記のスピン名を採用した。
<回転の合成>
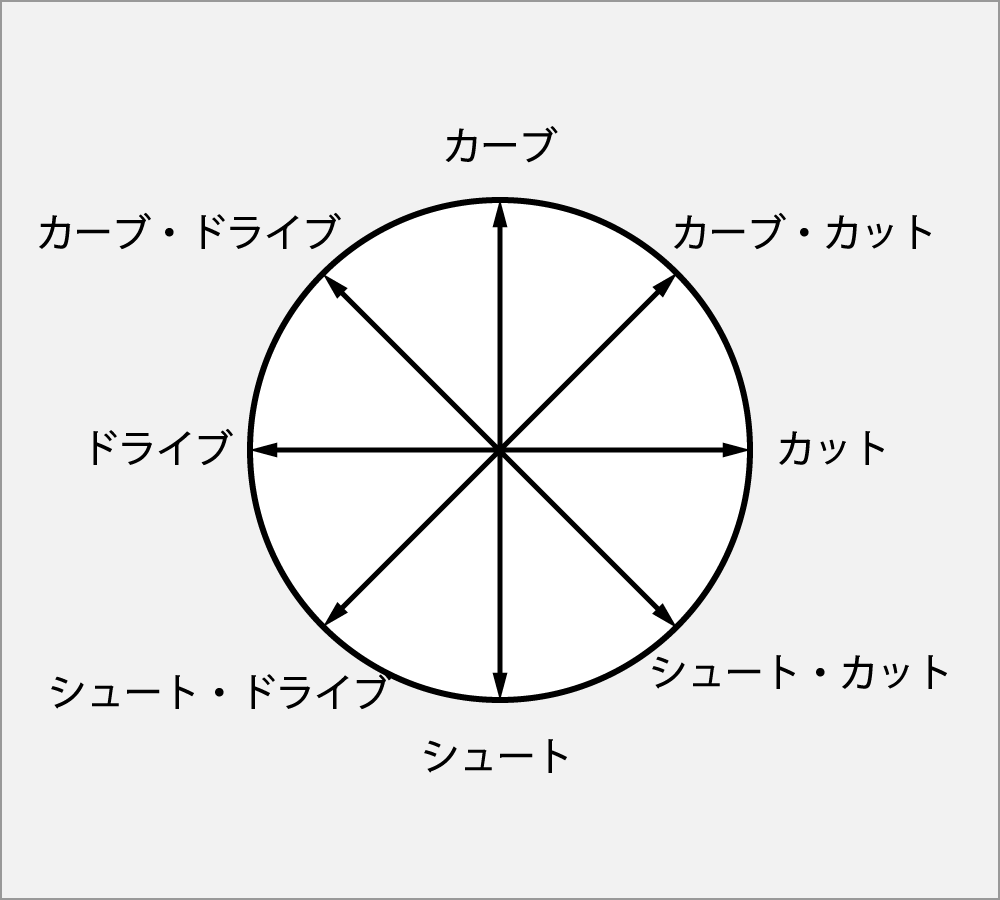
更に、カーブとカットとを含んだ回転は、カーブ・カットと呼ぶ。
あるいは、シュートとカットとを含んだ回転は、シュート・カットと呼ぶ様に、二つ以上の回転も表現できる。
左右軸と上下軸で構成する面の二つの回転を含んだ回転名を例として掲げる。
注記)カーブ・ドライブもドライブ・カーブも同じ回転であるが、
本書では二つ以上の回転の命名原則として前後軸・上下軸・左右軸の順とする。
当然であるが該当の回転が無ければ省く。
回転を相手の立場で見た時はΘ(相手視点のシータあるいは単にシータと呼ぶ)を付けることにする。本書ではΘはマイナスの意味として使っている。
マイナスは(-)で3文字使うが。これをΘで表すと1文字で済むからだ。
相手が繰り出すドライブ回転はΘドライブと呼び、その回転を自分の側から見るとカットとなる。
したがって、相手の回転を自分の回転に直すと、
Θドライブ = カット (ΘT = B)となる。同様に、
Θカット = ドライブ (ΘB = T)
ΘHコーク = Fコーク (ΘH = F)
ΘFコーク = Hコーク (ΘF = H)
横回転については、相手の回転と自分の回転は同じだ。なぜなら、上下軸は相手も自分も同じ軸を見ているからだ。
Θカーブ = カーブ (ΘR = R)
Θシュート = シュート (ΘL = L)
横回転と縦回転との合成の例を幾つか記しておこう。
また、Θは頭に一つだけ付けることにする。
Θカーブ・カット = カーブ・ドライブ (ΘRB=RT)
ΘHコーク・カット = Fコーク・ドライブ (ΘHB=FT)
Θシュート・ドライブ = シュート・カット (ΘLT=LB)
ΘFコーク・ドライブ = Hコーク・カット (ΘFT=HB)
明らかに、相手が出していると分かり、回転が立場で変わらないカーブやシュートの場合はΘを省くことがある。
回転の合成は回転と回転の足し算なので、ベクトルで正式に表記すると「+」となるが「・」で表記している。例えばカーブとドライブとを合成した回転ベクトルはカーブ + ドライブであるが、カーブ・ドライブと表記している。
また、英語の頭文字表記で表記するときは、その「・」も省略している。この例ではカーブ(R)とドライブ(T)との合成ベクトルはR+TであるがRTと表記している。
2.1.2 ベクトルによる戦術図
それでは、手っ取り早く、具体例で説明しよう。
戦術図の見方には幾つか約束がある。
- 球の矢印は、自分の側から見た球の回転ベクトルを示している。
- 黒いベクトルは「相手→自分」に向かう回転で緑と赤のベクトルを加えた結果の回転ベクトルとなっている。また、細く黒の破線はその回転の経路を示している。
- 赤いベクトルは自分もしくは相手が「ラケットで加える回転」だ。最初の打球は赤で始まるが煩雑さを避ける為に省略する場合がある。
- 緑のベクトルは「自分→相手」に向かう回転で、黒と赤のベクトルを加えた結果の回転ベクトルとなっている。また、細く緑の破線はその経路を示している。
- ○枠の番号は球の打球の順番を示している。
- □枠の番号は球の飛びの順番を示している。
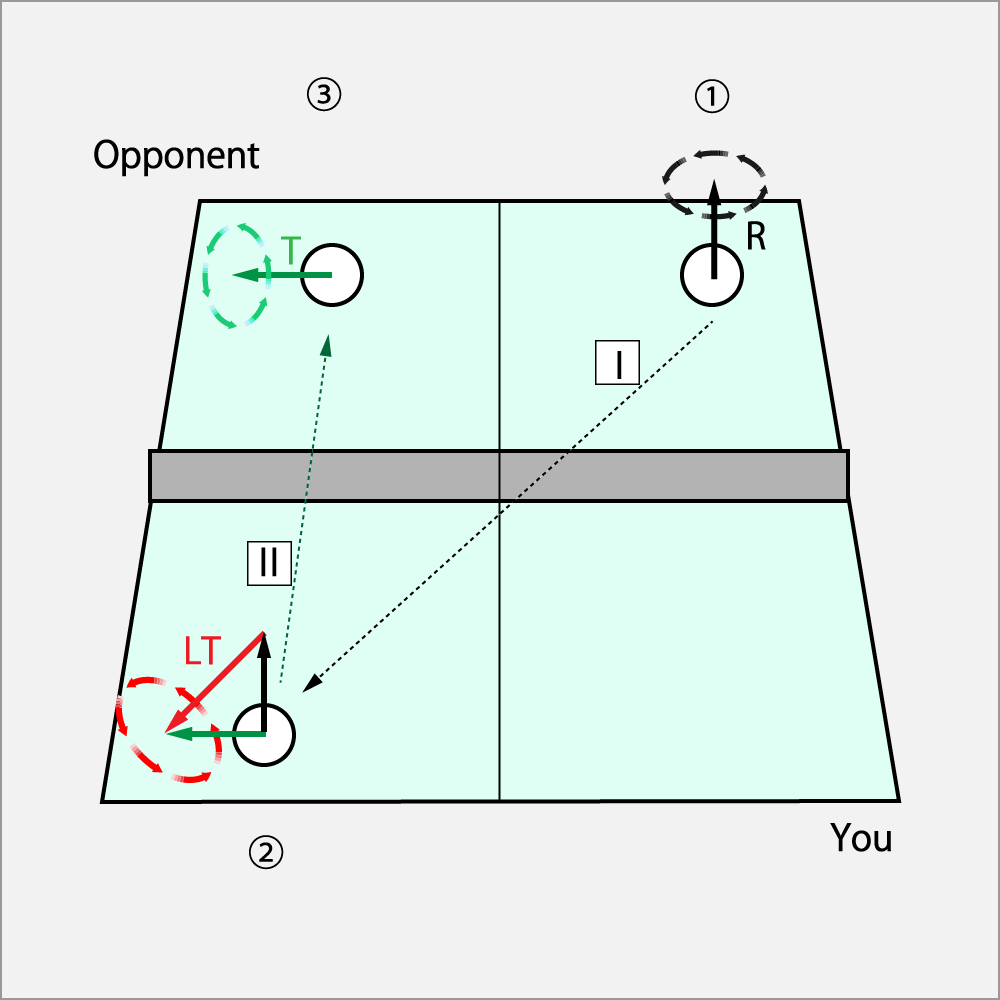
それでは、打球の順番を追って見てみよう。
① 相手がΘカーブ(ΘR)の球を出した。
② 自分のコートに入ったⅠの回転にシュート・ドライブ(LT)を与える。
③ 相手のコートにはⅡのドライブ(T)で返球される。
方程式は以下の通りとなる。
カーブ回転 + シュート・ドライブ回転 = ドライブ回転
英語の頭文字で表記すると,
R + LT = T
<ベクトル図>
ベクトル図の矢印は、右ねじの方向を示している。
黒いベクトルは、相手の加える回転ベクトル。
赤いベクトルは、自分の加える回転ベクトルだ。
緑は黒と赤のベクトルを加えた結果の回転ベクトルとなっている。
相手の回転ベクトル①から、送りたい回転ベクトル③、とを結ぶ回転ベクトル②が自分が加える回転だ。
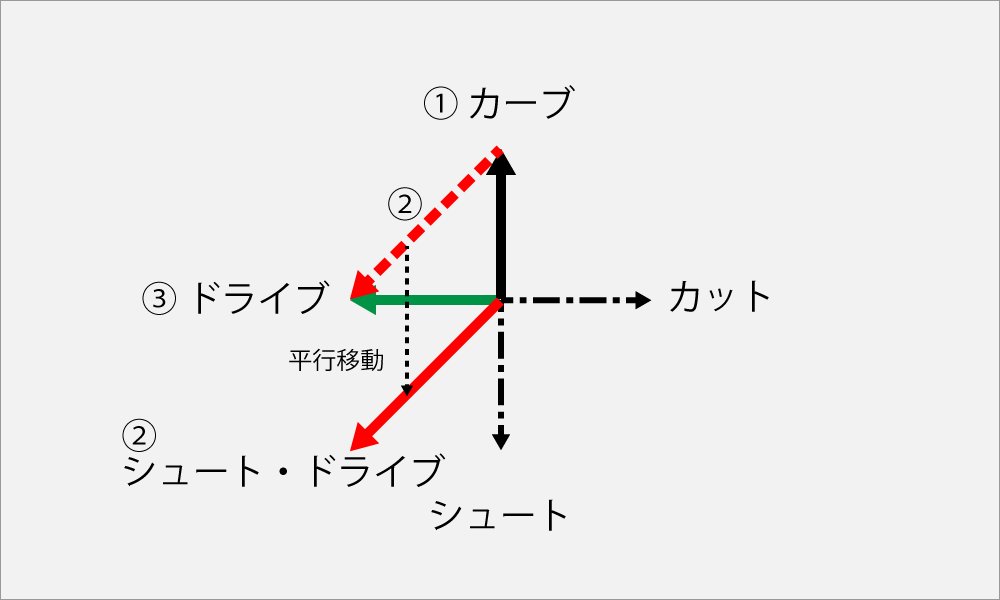
ここで注意がある。
カーブ回転とドライブ回転を繋いだらカーブ・ドライブではないかと思ってはいけないのだ。
回転の呼称の仕方が間違っているのだ。ベクトルの呼称は原点を基準としている。
だからこの場合は、カーブからドライブを結んだ赤い線を原点まで平行移動する。
したがって、このベクトルはシュート・ドライブとなる。
2.1.3 回転を考える道具

三次元の回転の合成を頭で考えるのは難しく間違いが多い。
そこで、私は製図用のデバイダーを購入し、両方の針を抜いて道具を作った。
相手からの球の回転に自分が球に加える回転を考え、机上で戦略を立てることが出来るのだ。
上のベクトル図に当てはめると、上向きのベクトル ←IN をカーブとし、左向きのベクトル ←OUTをドライブとする時、INからOUTへ結んだベクトルが加える回転ベクトルのシュート・ドライブとなる。また、返球する回転をドライブとする時、OUTベクトルの向きは常に左方向を向いている。
それでは、応用編に移ろう。相手からの振り方、 あるには自分のサービスに対する相手の返球パターンから相手球の回転は予測出来るので、 それに対応した最適な返球を用意した。これは、普段、私が使っている実証済みのオプションだ。