7.1. Tactic Diagram by Vector
In the tactical chart handled here, the rotation of a ball is represented by spin vectors. because it would be too complicated by the previous expression style to think of complicated problems.
How to read the diagram
- The number in a circle frame indicates the hitting order.
- The number in a square frame indicates the trajectory order.
- Vectors have each English initial letter to indicate the spin direction. Since we cannot draw three-dimensional spins in a two-dimensional figure, we are to get the image of a spin in the three dimention by using the initial letters. Knuckles are indicated by K, and are indicated by dots in the figure.
- A red vector is the spin imparting to the ball with a racket by you. A green one is a spin towards "you → the opponent". As a result of adding the red vector to the black one, it turns into a green one and returns to the opponent.
- A orange vector is the spin imparting to the ball with a racket by the opponent. A black one is a spin towards "the opponent → your". As a result of adding the orange vector to the green one, it turns into a black one and returns to you.
Concrete example < The Tactic to Draw a Triangle on a Wall against LongPips >
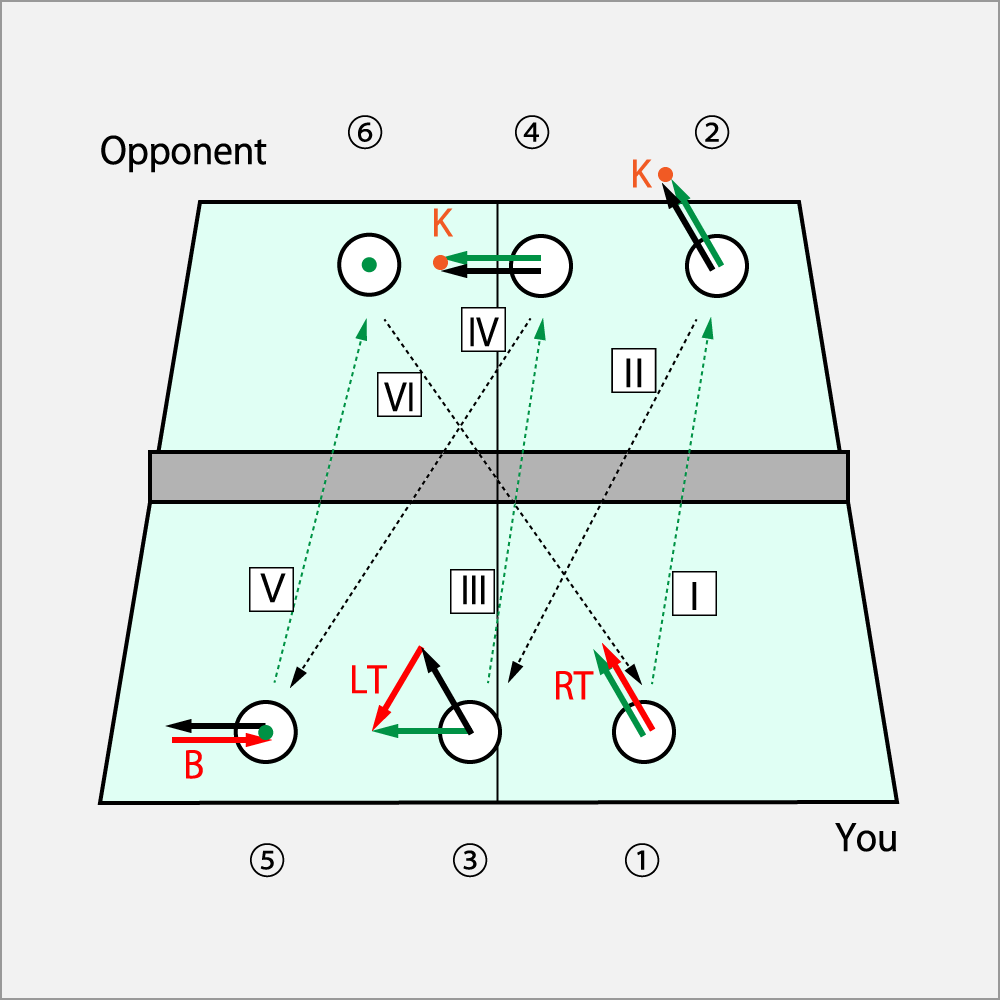
①. Make a service by Curve⋅Drive (RT).
Against your service of Curve⋅Drive (RT) on the trajectory-1, since the opponent of Long-Pips receives it by Knuckle (K),
the spin on the trajectory-2 returns with keeping the Curve⋅Drive (RT) .
③. Make a offensive return by Shoot⋅Drive (LT).
Imparting the spin by Shoot⋅Drive to the Curve⋅Drive (RT) on the trajectory-2,
it becomes Drive (T) on the trajectory-3 and returns to the opponent.
⑤. Make a defensive return by Cut (B) or juggling.
The spin on the trajectory-4 from the opponent returns as a ΘCut (ΘB).
If you return it by Cut (B) or juggling, it will be a Knuckle (K) on the trajectory-5.
Providing the opponent could receive well, it will return to the state of the hitting point-1, from the trajectory-6.