7.2. Consideration of Spin Composition and Vector Notation
Here, we will consider how to translate the knowledge of 1.11 "Rotational Expression between Ball and Swing Speed" into countable notation vectors on tactical diagrams in Part 2. "Think Tactics acoording to Vectors".
Since the rotation vector is a force, tracing the original rotation does not mean that a force has been applied, and is an invalid vector that does not accelerate the rotation. You need to subtract that amount from the rotation you tried to add. The resulting vector must take that into account.
When the ball's initial spin is fast and the next racket swing to rotate the ball is slow, since the ball cannot move the racket, the difference of the speed is converted into flight by the reaction force. In view this point, it is desirable to represent with vectors.
For ease of understanding, the first half will be explained in one dimension and the second half will be explained in two dimensions.
This section consists of the following.
7.2.1. One-dimensional vector composite notation
7.2.1.1.When rubbing forward at an angular velocity faster than the initial one
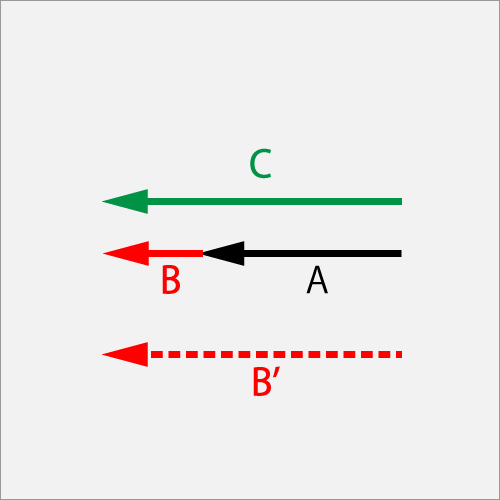
Vector A is a ball initial anguluor-velocity of ΘCut(1.0T). vector B' is a racket swing of Drive(1.5T). As a result of rubbing the ball with the racket, the ball's final spin will be vector C of Drive(1.5T). Acceleration vector is the B: Drive (0.5T).
7.2.1.2. When rubbing forward at the same angular velocity as the initial one
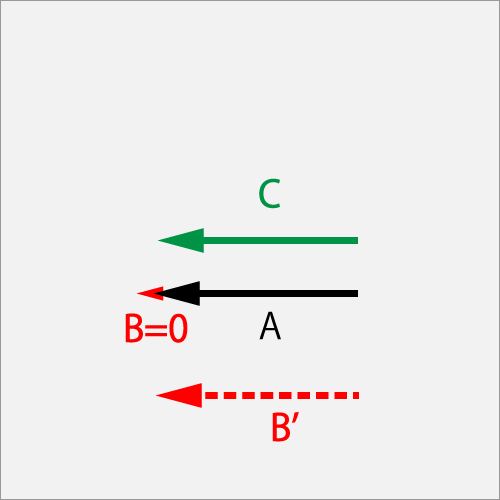
Vector A is a ball initial angulor-velocity of ΘCut(1.0T). vector B' is a racket swing of Cut(1.0T). As a result of rubbing the ball with the racket, the ball's final spin will be vector C of Cut(1.0T) keeping the same spin. Acceleration vector is B(0.0) which does not contribute to make a spin.
7.2.1.3. When rubbing forward at an angular velocity lower than the initial one
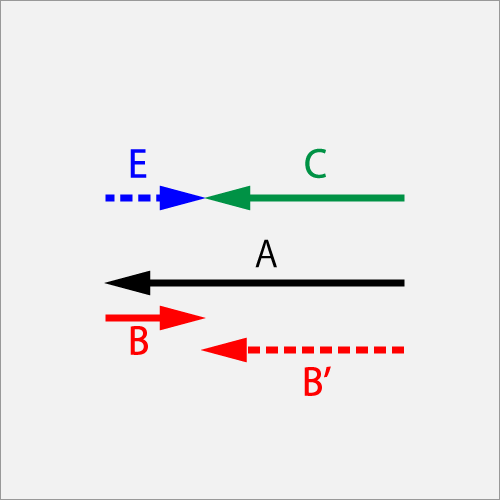
Vector A is a ball initial angulor-velocity of ΘCut(1.0T). Vector B' is a racket swing of Drive(1.5T). As a result of rubbing the ball with the racket, the ball's final spin will change to vector C of Drive(1.5T). Acceleration vector B(0.5B) which is the difference between the A and B changes to the flight vector E (0.5). The ball receives the reaction-force from the rubber instead of moving the racket.
7.2.1.4. When the ball flying at the initial angular velocity hits a stopped racket
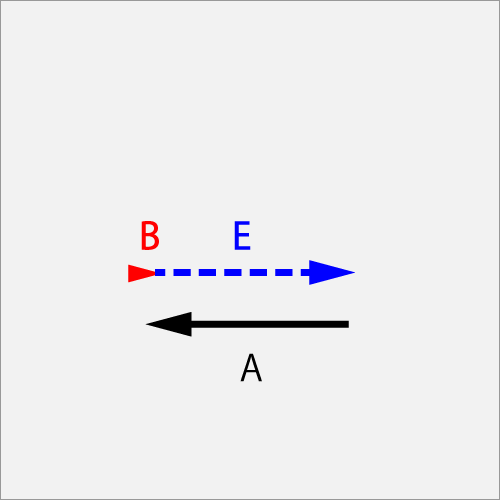
Vector A is a ball initial angular-velocity of ΘCut (1.0T), Vector B is a racket swing of zero angular-velocity (0.0B) that is fixed not moving.
As a result of hitting the ball with the racket, the ball will stop the spin and change to the flight vector E (1.0).
7.2.1.5. When rubbing reverse at an angular velocity lower than the initial one
When rubber does not slip
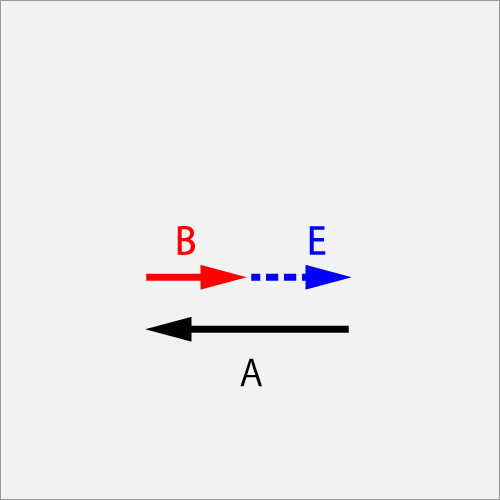Vector A is a ball initial angular-velocity of ΘCut (1.0T), vector B is a racket swing of Cut (0.5B), As a result of hitting the ball wit the racket, the ball will stop the spin and change to the flight vector E (0.5).
When the rubber slips
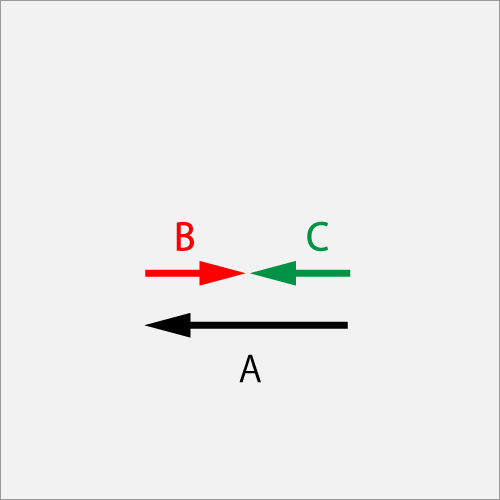Vector A is a ball initial angular-velocity of ΘCut (1.0T), vector B is a racket swing of Cut (0.5B)As a result of hitting the ball with the racket, the spin will be changed to vector C of Drive (0.5T).
7.2.1.6. When rubbing reverse at the same angular velocity as the initial one
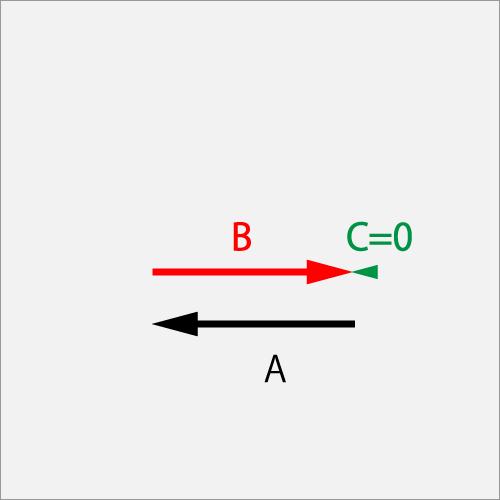
Vector A is a ball initial angulor-velosity of ΘCut(1.0T), vector B is a racket swing of Cut (1.0T).
As a result of hitting the ball with the racket, the A and B cancel each other, the spin will stop the rotation and become vector C of Knuckle (0.0).
7.2.1.7. When rubbing reverse at an angular velocity ω (t) of 1.5 times faster than the initial one
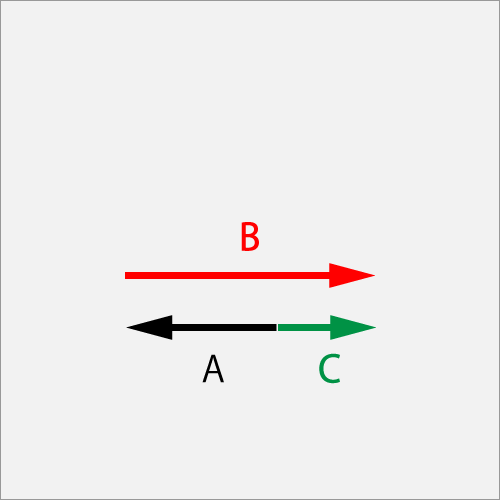
Vector A is a ball initial angular-velosity of ΘCut (1.0T), vector B is a racket swing of Cut-B (0.5B).
As a result of rubbing the ball with racket, the difference of the A and B remains, the ball's final spin will be vector Cof Cut (0.5B).
7.2.2. Composite notation of two-dimensional vectors
7.2.2.1. When rubbing with a Durve⋅Drive (0.71R + 0.71T) against the ΘCut (1.0T)
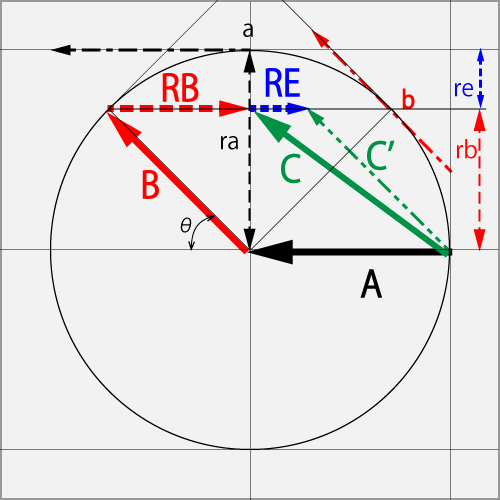
How to read the figure
In this figure, three dimensions are expressed in two dimensions, and the ball is viewed from your front. Lowercase letters a and b are the points on the ball's front, and ra, rb, and re represent lengths as viewed from the front. The same goes for the uppercase vectors A, B, C, RB, and RE. However, it is considered that the speed of rubbing the points a and b indicated by the dashed line of the thin line acts from the front to the back by the length viewed from the front.
Vector A is the angular momentum that is already rotating. The ball radius is "ra", and is the angular momentum when the unit "1" is applied to the point "a" with a black dot-dash line.
Vector B is the newly added angular momentum. It is the angular momentum when the force of a dot-dash line is applied to point b.
Vector RB is the angular momentum corresponding to the radius rb up to the point b, and is a component in the A direction of the vector B, which is a component of B that has traced A and has no effect on A. It is used for correction when added.
Vector RE is the angular momentum corresponding to the radius re to the point b, and is the remaining inertial momentum of A obtained by subtracting RB from A.
Vector C is the angular momentum obtained by adding the B to the A and further subtracting the RB.
The vector C' is shown for reference. This vector is the angular momentum resulting from further subtracting the RE from the C. This is the result when the remaining momentum of A is converted into flight. However, the rubber actually slips, and the rate at which RE converts to flight varies. Since there is not much difference in thinking about the strategy, in the strategic diagram, unless otherwise specified, it is treated as not converting to flight.
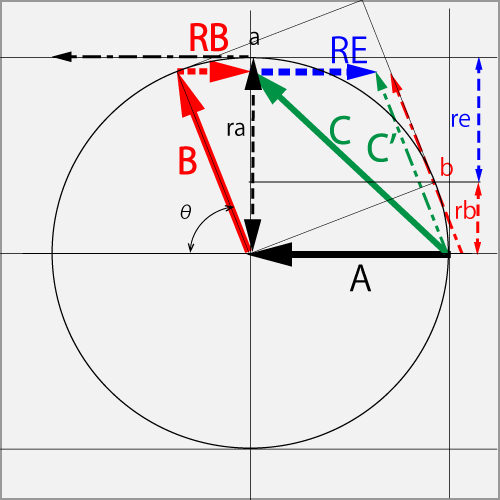
The following is my sense. There is a phenomenon,
whice takes C or C', that seems to change at the certain angle.
At the case that "A and B are the same size" and "the rubber uses a Non-slip".
If the Θ is the 45° or less, and (RB ≥ RE), the reaction force will be C'.
And if the Θ is the 45° or more, and (RB < RE), it keeps the rotation and becomes C .
Explanation of the figure
Against the ΘCut (1.0T) in vector A, the point b of the ball's lower-right side was rubbed by the Curve⋅Drive (0.71R + 0.71T) in vector B , and the spin has become to be the Curve⋅Drive (0.71R + 1.0T) in a total-vector C.
So the total vector C is obtained by subtracting the RB of Vector B, which is the same directional component as the initial vector A, from the vector obtained by adding the A and B.
C = A + B - RB
Another expression
This figure has the same contents as the previous figure. First, subtract the RB from the A, then add it the B to derive the C. This expression is also used is some sections.
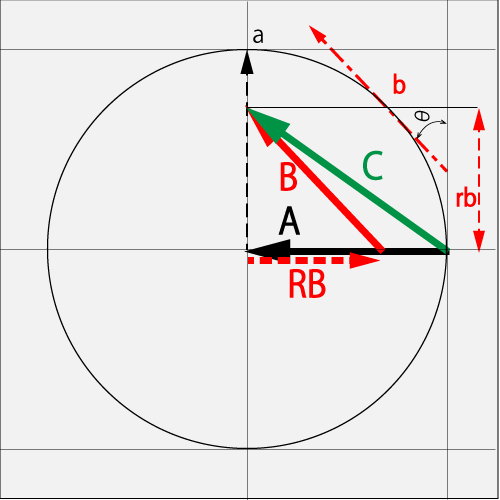
7.2.2.2. When rubbing with a Curve⋅Drive (0.2R + 1.0T) against the ΘCut (1.0T)
Against the ΘCut (1.0T) in vector A, if the point b of the ball's upper-right side was rubbed by a Curve⋅Drive (0.2R + 1.0T) in vector B, and the spin has got the Curve⋅Drive (0.2R + 1.0T) in a total vector C.
So the total vector C will be obtained by subtracting the RB of Vector B, which is the same directional component as the initial vector A, from the vector obtained by adding the A and B.
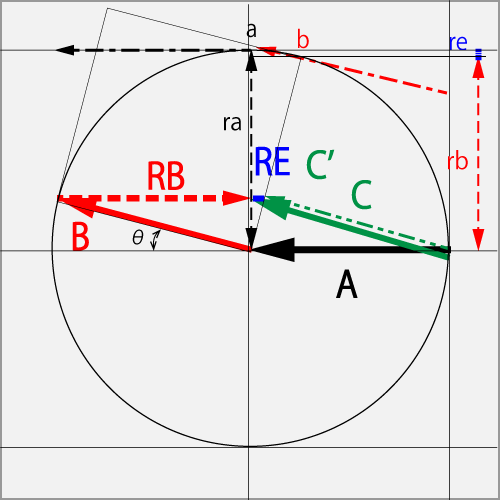
7.2.2.3. When rubbing with a Curve⋅Drive (1.0R + 0.4T) against the ΘCut (1.0T)
Against the ΘCut (1.0T) in vector A, if the point b of the ball's upper-right side was rubbed with a Curve⋅Drive (1.0R + 0.4T) in vector B, and the spin has become the Curve⋅Drive (1.0R + 1.0T) in a total vector C.
So the total vector C will be obtained by subtracting the RB of Vector B, which is the same directional component as the initial vector A, from the vector obtained by adding the A and B.
7.2.2.4. When rubbing with a Curve (1.0R) against the ΘCut (1.0T)
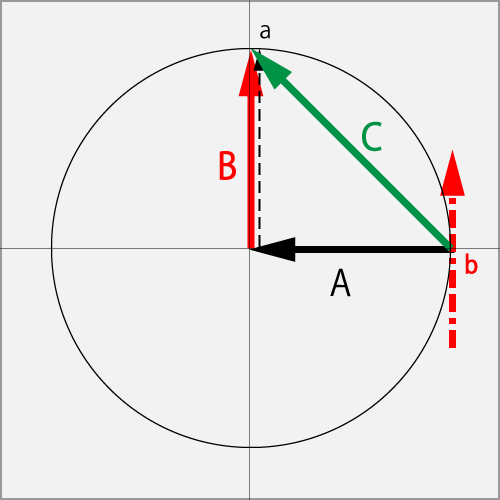
Against the ΘCut (1.0T) in vector A, if the point b of the ball's right side was rubbed by a Curve⋅Drive (1.0B) in vector B, and the spin has become the Curve⋅Drive (1.0R + 1.0B) in a total vector C. So an acceleration vector can be considerded the Cut (1.0B) in vector B.
The red vector of the dashed line is the apparent virtual vector of vector B, and indicates the location and size of the rubbed ball.
7.2.2.5. When rubbing with a Curve⋅Drive (1.0R + 1.0T) against the ΘCut (1.0T)
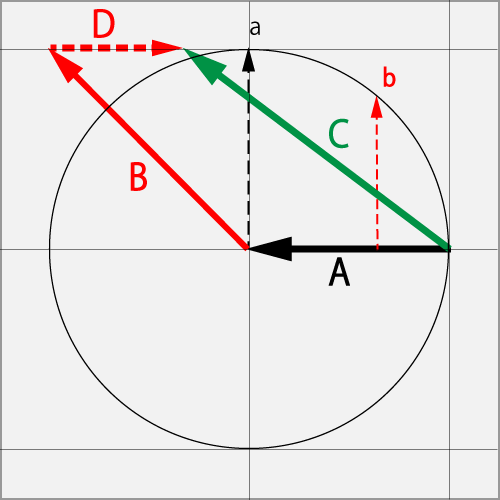
Against the Curve (1.0R) in vector A, if the point b of the ball's under right side was rubbed by a Curve⋅Cut (1.0L+1.0B) in vector B, and the spin has become the Curve⋅Cut (1.0R + 1.25B) in a total vector C.
If vector B includes a Curve component D of the initial vector A, vector C will be obtained by subtracting the D from the vector obtained by adding the A and the B.
Here, the virtual vector B' of vector B is omitted because it does not fit in the figure.
7.2.2.6. When rubbing with a Curve⋅Cut (0.5R + 1.0B) against the ΘCut (1.0T)
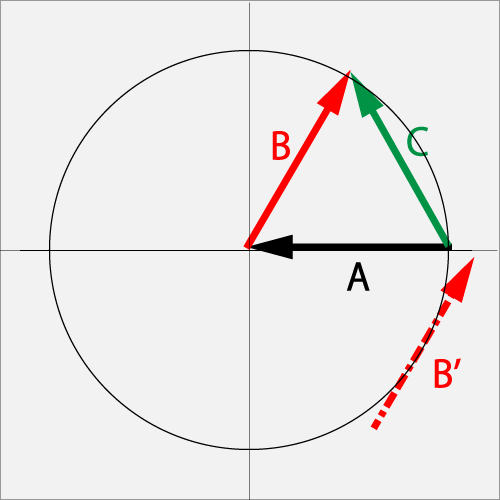
Against the Curve (1.0R) in vector A, if the point B' of the ball's under right side was rubbed by a Shoot⋅Cut (1.0R+1.0B) in vector B , and the spin has become the Shoot⋅Cut (1.0L + 1.0B) in a total vector C. So vector B is called Acceleration vector.
Vector B' is the virtual vector of Vector B.
7.2.2.7. When rubbing with a Curve⋅Cut (1.0R + 0.5B) against the ΘCut (1.0T)
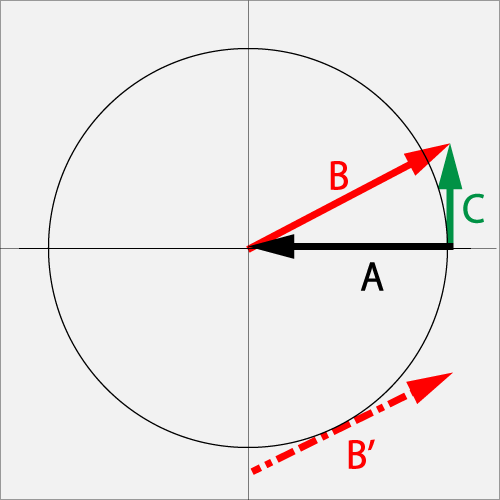
Against the Curve (1.0R) in vector A, if the point B' of the ball's under right side was rubbed by a Shoot⋅Cut (1.0R+0.5B) in vector B , and the spin has become the Cut (0.5B) in a total vector C. So vector B is an acceleration vector.
Vector B' is the virtual vector of Vector B.