7.1 ベクトルによる戦術図

この節で扱う戦術図は、球の回転はベクトル図で表している。複雑な問題を思考するのには、従来の球に回転方向を図示した方法では煩雑になりすぎるからだ。

少し、説明しておこう。

○枠の数字は打順を示している。
□枠の数字は球の進む順番を示している。
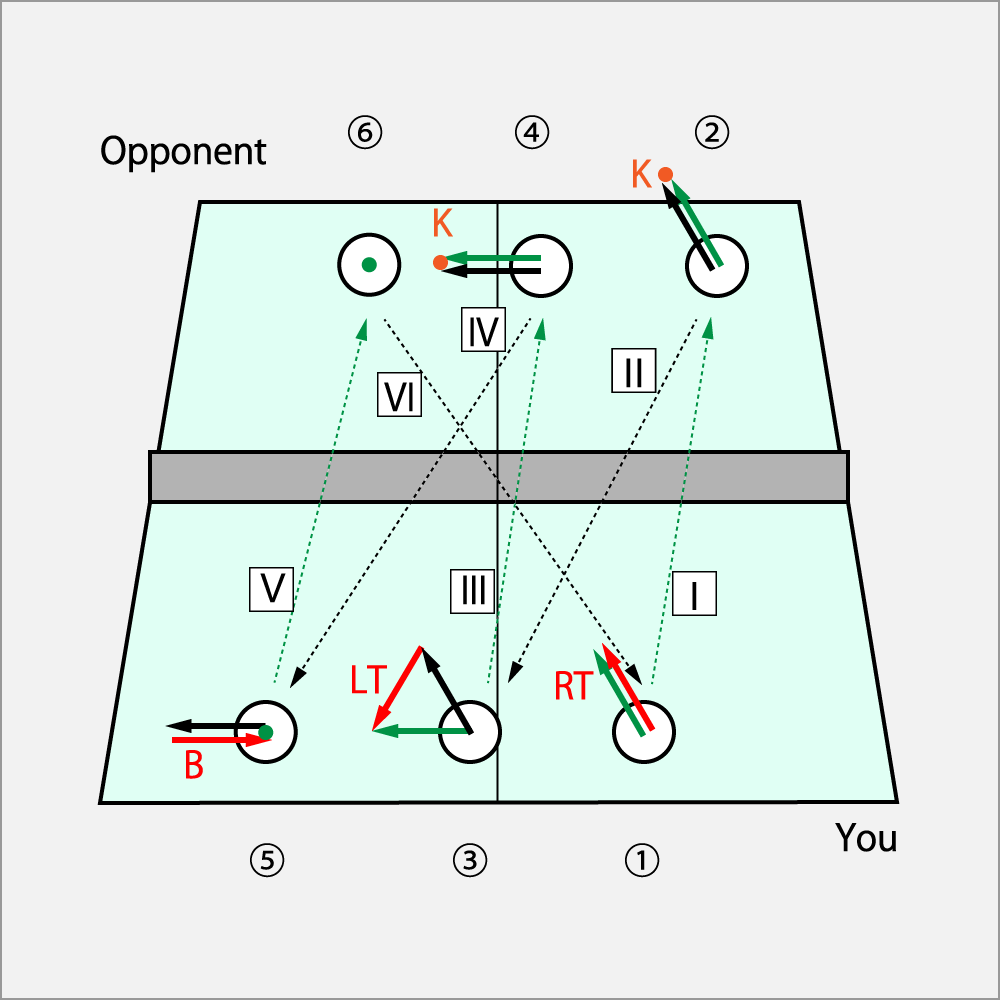
ベクトルには回転を示す英語の頭文字で表記している。２次元の図に３次元の回転を描くことが出来ないので、回転はこの頭文字で考える。なお、ナックルはKで表し、図ではドットで表示している。
赤色のベクトルは「君がラケットで加える回転」、緑のベクトルは「自分→相手」に向かう回転だ。黒の回転に君が赤の回転を加えた結果、緑の回転となって相手に戻る。
オレンジ色のベクトルは「相手がラケットで加える回転」。黒のベクトルは「相手→自分」に向かう回転だ。
緑の回転に相手がオレンジの回転を加えた結果、黒の回転となって自分に戻って来た。

具体例　＜粒高に対する「壁に描く三角作戦」＞

①　 カーブ・ドライブでサーブする。
Ⅰのカーブ・ドライブのサーブに対して、相手が粒高でレシーブする、即ちナックルでレシーブするので、Ⅱではカーブ・ドライブがそのまま戻ってくる。

③　シュート・ドライブで打ち抜く。
Ⅱのカーブ・ドライブに対してシュート・ドライブを加えて、Ⅲのドライブとして相手を打ち抜く。

⑤　カットもくしはシャクリで攻撃的に繋ぐ。
相手のブロックは、ⅥのΘカットとなって戻ってくるので、攻撃的なカットもしくはシャクリによって返すと、Ⅴでナックルとなる。　相手がうまくレシーブできれば、それはⅥで①の状態に戻ることになる。