Part 2. Think Tactics acoording to Vectors
2.6. Control the Return Directions
If you can't control the direction of the ball well, the direction of the return ball will be monotonous and you will not be able to beat your opponent.
By controlling the return direction, it is possible to return to a place beyond the opponent's defensive range and create a gap in the opponent's attack.
Let's return to Section 1.9.1 "Relation between the Ball and the Swing".
2.6.1. Steer in the Return Direction by Rotating the Waist
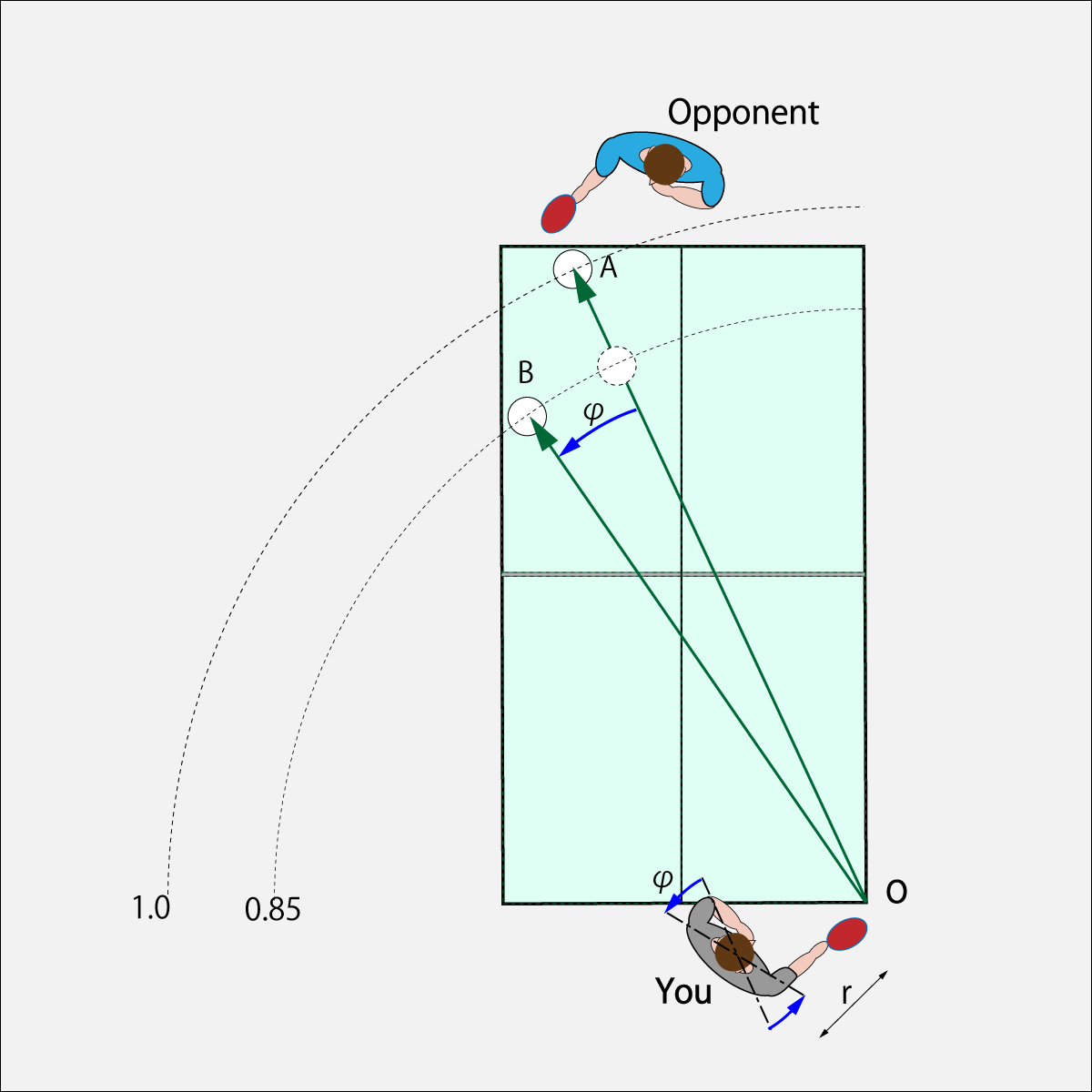
Let's return to Section 1.9.1 "Relationship between the ball and the swing".
The ball basically flies in the tangential direction of the swing. If the direction of the ball flies in the A direction when the rotation of the waist is not conscious, the direction is guided by the rotation of the waist in order to fly in the B direction.
If the direction of B is from the direction of A to the direction of φ, the rotation angle of the waist is also φ. At that time, since the flight distance of A is too large, the radius of gyration r of the swing is shortened to adjust the flight distance.
2.6.2. Steer with Directional Correction Vector
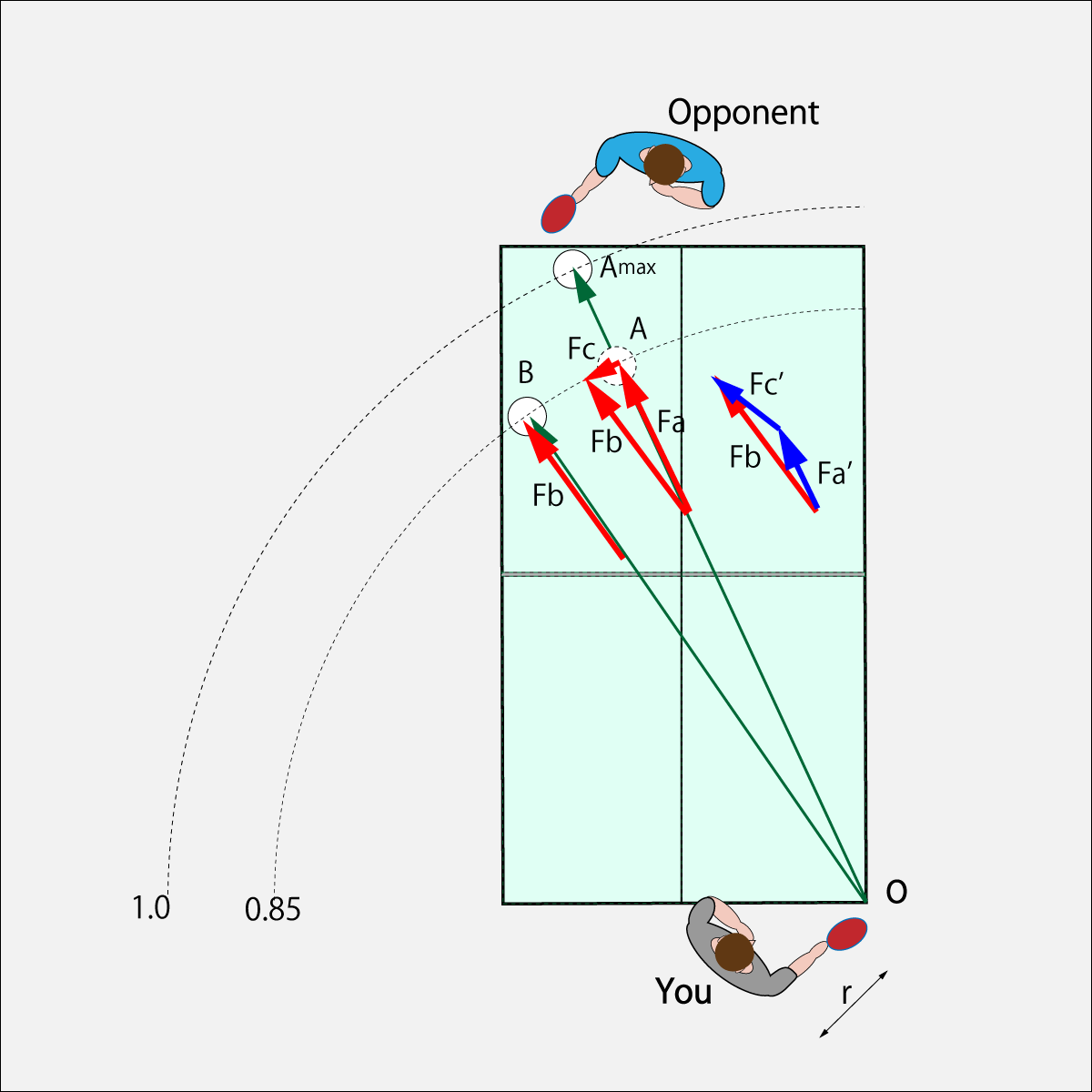
You may want to change direction in the middle of a swing. Let's explain the case of changing the direction from the A direction to the B direction.
When aiming at point B, the force of Fb shall be applied. Since the force aiming at the Amax point will come out of the table, it can be made into the force of Fb by adjusting the force to lower it to Fa and then applying the force of the direction correction vector Fc perpendicular to the initial swing direction. In this case the correction vector would be rubbed with a Fcork⋅Curve⋅Drive. The force is adjusted by the radius of the swing.
There are various combinations of Fb vector forces aimed at point B. Change the amount of Fa and Fc according to the situation. As another example, the example of Fa'and Fc' is described.
It takes courage to add a correction vector at first, as it may jump over the sideline. However, if you try the correction vector without thinking hard, you will get used to the force.