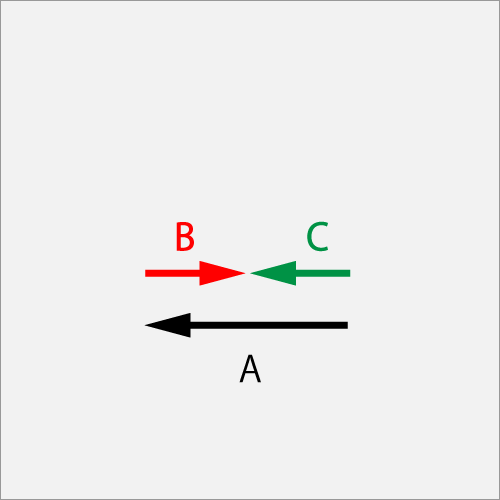
7.2 スピン合成とベクトル表記の考察
ここでは、1.11節「方程式からみた球とラケットの回転速度」の知見を2部以降の戦術図のベクトルの可算表記に落とし込む方法を検討するものだ。
回転ベクトルは力なので、元の回転をなぞっても力を加えたことにはならず、球の回転を加速しない無効ベクトルとなり、加えようとした回転からその分を差し引く必要がある。結果のベクトルはそれを考慮したものでなければならない。
また、球の元の回転が速く、次に回転を加えるラケットの動きが遅い時、球はラケットを動かすことが出来ないとすると、反作用でその差分が飛びに変換する。その点を考えてベクトルは表記されるのが望ましい。
理解し易くするために、前半に一次元で説明し、後半に二次元で説明する。
本節は以下で構成されている。
7.2.1 一次元ベクトルの合成表記
7.2.1.1 初速Aより速い角速度B'で順回転方向へ擦った場合
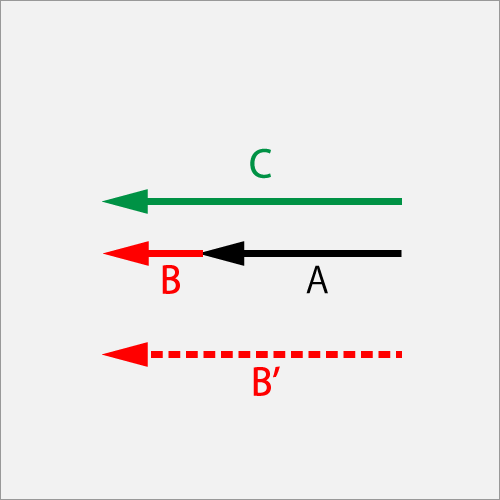
AのΘカット(1.0T)に対してB'のドライブ(1.5T)で擦った結果Cのドライブ(1.5T)となった。加速ベクトルはBのドライブ(0.5T)となる。
7.2.1.2 初速Aと同じ速さの角速度B'で順回転方向へ擦った場合
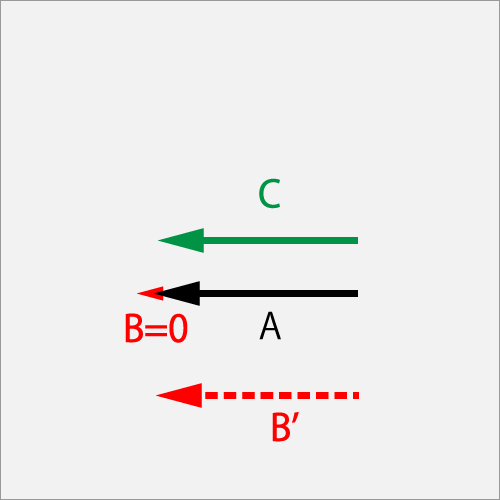
Aのカーブ(R)に対してB'のカーブ(1.0R)で擦った結果Cのカーブ(1.0R)のまま変わらない。加速ベクトルBは0となり回転に寄与しない。
7.2.1.3 初速Aより遅い角速度B'で順回転方向へ擦った場合
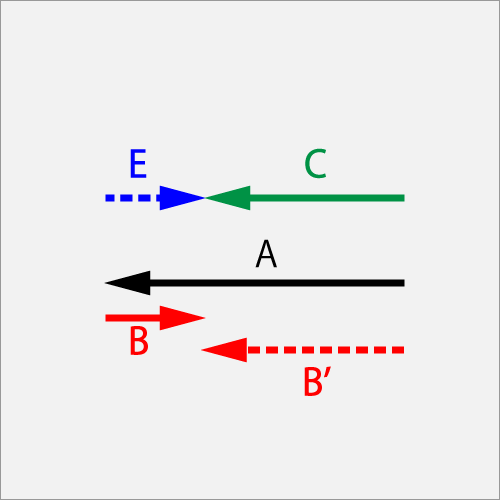
AのΘカット(1.5T)に対してB'のドライブ(1.0T)で擦った結果Cのドライブ(1.0T)となった。AとB'の差分Bの加速ベクトル(0.5)は、ラケットを動かす代わりにラバーの反作用受けてEの球の飛びとなった。
7.2.1.4 初速Aの角速度が停止してるラケットに当たった場合
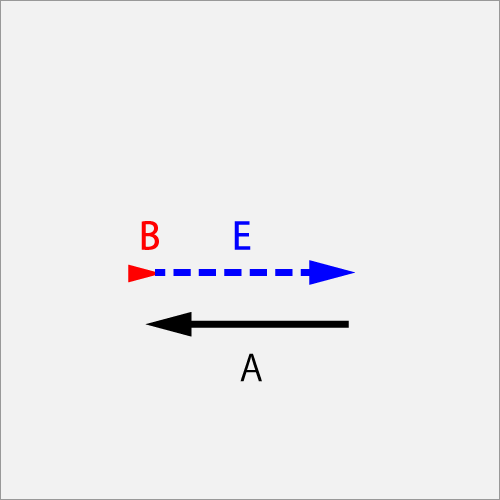
AのΘカット(1.0T)に対してBの角速度がゼロ(0.0B)のラケットに当たった結果、球は回転を止めてEの飛び(1.0T)となった。
7.2.1.5 初速Aより遅い角速度Bで逆回転方向へ擦った場合
ラバーが滑らない時
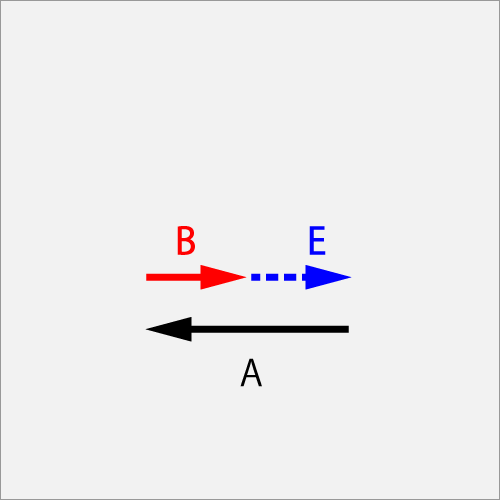
AのΘカット(1.0T)に対してBのカット(0.5B)で擦った結果、球は回転を止めEの飛び(0.5)となった。
7.2.1.6 初速度Aと同等な角速度Bの逆回転方向へ擦った場合
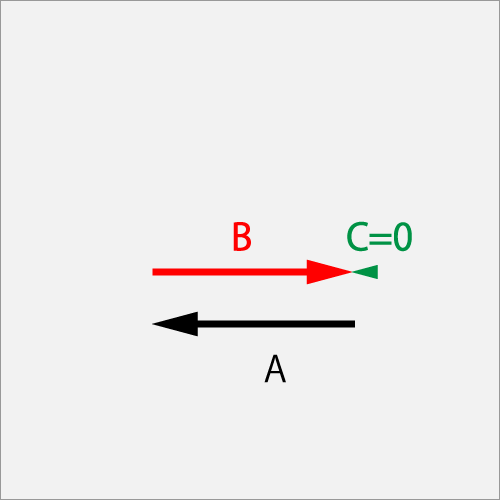
AのΘカット(1.0T)に対してBのカット(1.0T)で擦った結果Cの回転ゼロのナックル(K)となった。
7.2.1.7 初速Aより1.5倍速い角速度ω(t)で逆回転方向へ擦った場合
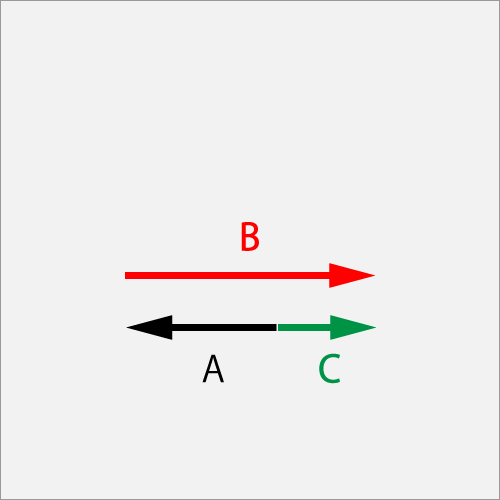
AのΘカット(1.0T)に対してBのカット(1.5B))で擦った結果Cのカット(0.5B)となった。
7.2.2 二次元ベクトルの合成表記
7.2.2.1 Θカット(1.0T)に対しカーブ・ドライブ(0.71R+0.71T)で擦った時
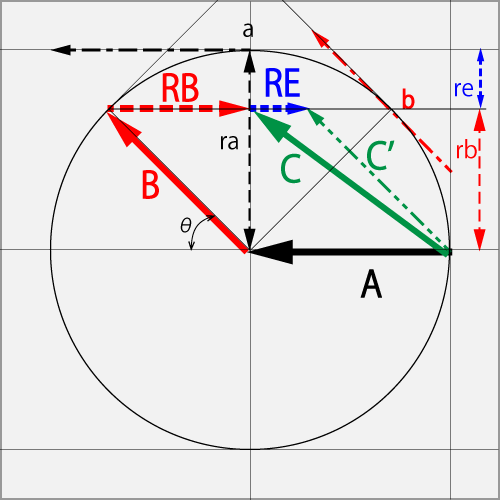
図の見方
この図は3次元を2次元で表現しており、球を正面から見ている。小文字のa、bは正面の点であり、ra、rb、reは正面から見た長さを表している。大文字のベクトルA、B、C、RB、REも同様だ。しかし、細線の一点鎖線で示したa点・b点を擦る速度は、正面から見た長さで正面から裏面へ作用していると見る。
ベクトルAは既に回転している角運動量である。球の半径raであり、点a対して単位"1"を黒い一点鎖線の力を与えた時の角運動量、
ベクトルBは新しく加える角運動量である。点bに対して単位"1"の赤い一点鎖線の力を与えた時の角運動量だ。
ベクトルRBは、b点までの半径rbに相当する角運動量であり、ベクトルBのA方向成分で、BがAをなぞった分でありAに影響を与えていない成分で、単純にAにBを加えた場合の補正に使う。
ベクトルREは、b点までの半径reに相当する角運動量であり、AからRBを差し引いたAの残りの慣性運動量だ。
ベクトルCはベクトルAにベクトルB加え、更にベクトルRBを差し引いた結果の角運動量である。
参考として
ベクトルC'はを示した。このベクトルはCから更にベクトルREを差し引いた結果の角運動量である。これはAの残りの慣性運動量が飛びに変換した場合の結果だ。
しかしながら、実際にはラバーに滑りがあり、REが飛びに変換する割合には幅がある。戦略を考える上でそれほどの差が無いので、戦略図では特記以外は、飛びには変換しないでものとして扱う。
以下は私の感じであるが、
現象がCかC'を取るかは遷移する特定の角度があるように思える。
「AとBの大きさが同じ」で「滑らないラバー」の時は、
θが45°以下で、(RB≥RE)ならば反力を受けC'となり、
45°以上で、(RB<RE)ならば回転を維持しCとなる。
図の解説
AのΘカット(1.0T)に対して、球の右下の点bをBのカーブ・ドライブ(0.71R+0.71T)で擦った、結果Cのカーブ・ドライブ(0.71R+1.0T)となった。
Bベクトルが元のAベクトルとの同方向の成分RBを含むときは、ベクトルAとBベクトルを加えたベクトルから同方向の成分RBを差し引いたC'ベクトルとなる。
C = A + B - RB
もう一つの表現
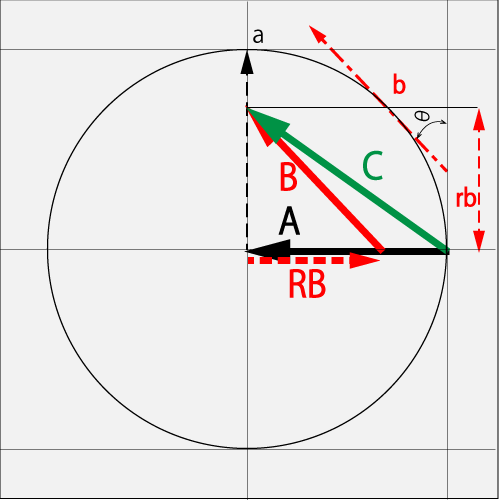
この図は先の図と同じ内容である。最初にRBを差し引いてからBを加えてCを導き出したものだ。この表現も使うので紹介している。
7.2.2.2 Θカット(1.0T)に対しカーブ・ドライブ(0.2R+1.0T)で擦った時
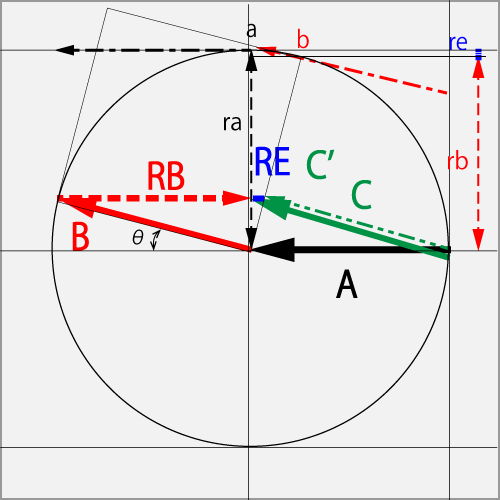
Aのカーブ(1.0R)に対して、球の右上の点bをBのカーブ・ドライブ(0.2R+1.0T)で擦った結果、Cのカーブ・ドライブ(0.2R+1.0T)となった。
Bベクトルが元のAベクトルの同方向の成分RBを含むときは、ベクトルAとBベクトルを加えたベクトルから同方向の成分RBを差し引いたCベクトルとなる。
7.2.2.3 Θカット(1.0T)に対しカーブ・ドライブ(1.0R+0.4T)で擦った時
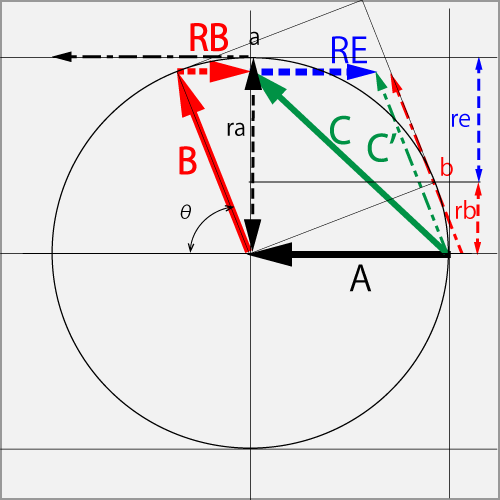
AのΘカット(1.0T)に対して、球の右上の点bをBのカーブ・ドライブ(1.0R+0.4T)で擦った結果、Cのカーブ・ドライブ(1.0R+1.0T)となった。
Bベクトルが元のAベクトルと同方向の成分RBを含むときは、ベクトルAとBベクトルを加えたベクトルから同方向の成分RBを差し引いたCベクトルとなる。
7.2.2.4 Θカット(1.0T)に対してカーブ(1.0R)で擦った時
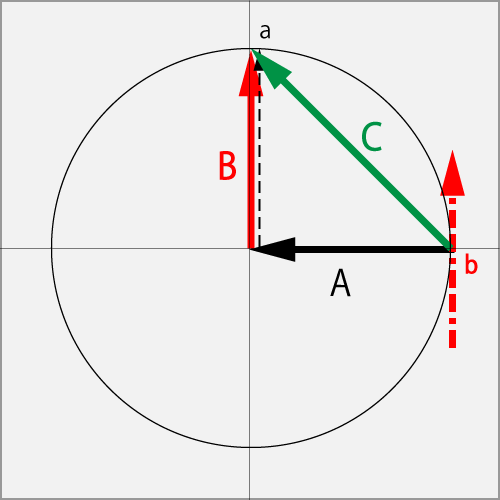
AのΘカット(1.0B)に対してb点をBのカーブ(1.0R)で擦った結果、Cのカーブ・ドライブ(1.0R+1.0T)となった。加速ベクトルはBのカーブ(1.0R)となる。
一点鎖線の赤いベクトルはBベクトルの見た目の仮想ベクトルであり、球の擦った場所と大きさを示している。
7.2.2.5 Θカット(1.0T)に対しカーブ・ドライブ(1.0R+1.0T)で擦った時
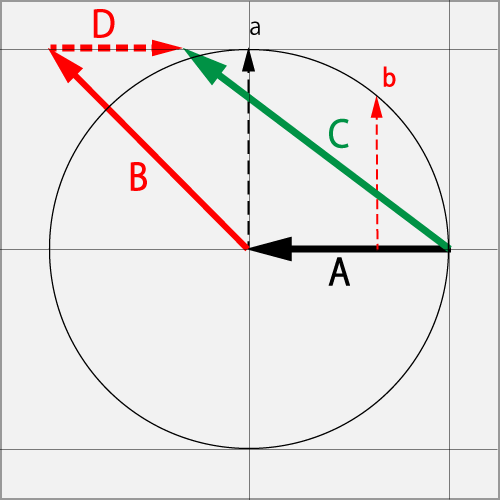
AのΘカット(1.0T)に対して、球の右下の点bをBのカーブ・ドライブ(1.0R+1.0T)で擦った結果、Cのカーブ・カット(1.0R+1.25B)をとなった。
Bベクトルが元のAベクトルと同方向の成分Dを含むときは、ベクトルAとBベクトルを加えたベクトルから同方向の成分Dを差し引いたCベクトルとなる。
ここで、図に収まらないのでBの仮想ベクトルは省略した。
7.2.2.6 Θカット(1.0T)に対しカーブ・カット(1.0R+0.5B)で擦った時
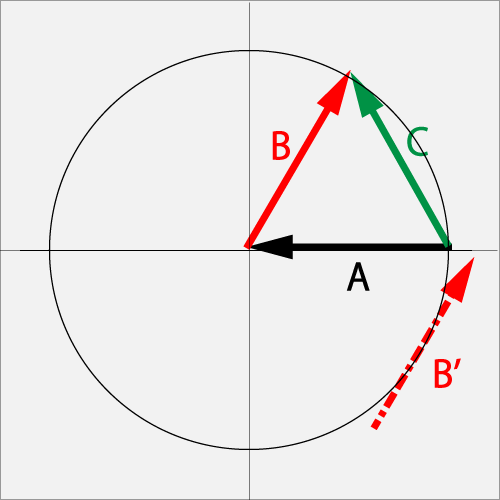
AのΘカット(1.0T)に対してB'点をBのカーブ・カット(1.0R+0.5B)で擦った結果、Cのカーブ(1R+0.5T)となった。加速ベクトルはBのカーブ・カット(1R+0.5B)となる。
7.2.2.7 Θカット(1.0T)に対しカーブ・カット(1.0R+0.5B)で擦った時
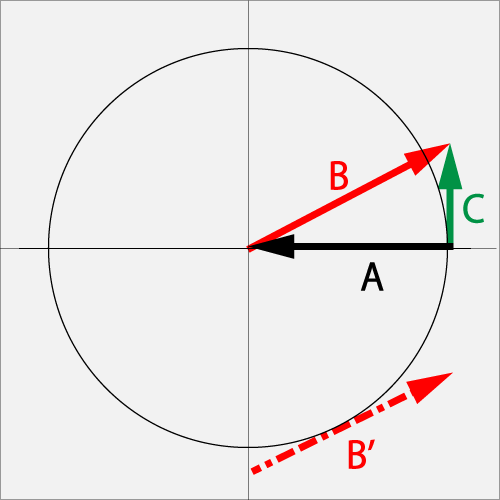
Aのカーブ(1.0R)に対してB'点をBのシュート・カット(1.0L+0.5B)で擦った結果、Cのカット(0.5B)となった。