ラバーの大切な要素は大きく二つある。一つはラバーの種類であり、二つ目はラバーの厚さだ。
そしてラバーの種類は大きく二つある。接触抵抗の少ない表ラバーと、接触抵抗の大きい裏ラバーだ。
表ラバーで打った球は「飛びの運動量」はあるが、「回転の運動量」が少ない。一方、裏ラバーで打った球には「飛びの運動量」と「回転の運動量」がある。
ラバーによって回転が大きく変わる。卓球を制するためには、回転を起こすラバーについて知る必要がある。
自分のラバーの性格と、相手のラバーの性格を知らねば、球は自分に意図した打球とならず、戦いにならない。
ラバーには厚さには、薄、中、厚、特厚の種類がある。厚くなるほど重くなる。
薄ラバーのラケットと厚ラバーの振りの速度を比較すると、薄ラバーの方は軽い分だけ振り易い。
薄ラバーと厚ラバーの違いは重さだけなのだろうか。何故、選手はラバーの厚さを選択するのだろうか。
何か基準が欲しい。そこで大まかに考えてみた。球はラバーによって弾む。その時、厚さはどう関係してくるのだろうか。
同じ材料のラバーを厚いのと薄いのとを机の上に置き、同じ高さから、球を落とすと、跳ね返りの高さがどう違うのだろうか。
君は厚い方が弾むと思っていないだろうか。結果は、同じなのだ。これはどういうことか。
ラバーに落ちて来た球はラバーを縮めることによりラバー内部に歪エネルギーを蓄える。
そして、縮んだラバーが復元する過程で、そのエネルギーを放出し球を跳ね返す。
だから、跳ね返した高さが同じということはラバー内部で放出したエネルギー量も同じだ。
しかしながら、ラバーの厚さが異なるので、ラバー内部の応力は異なる。薄いラバーの方が厚いラバーよりも内部応力が大きいのだ。
計算結果ではラバー厚さが2倍の時、内部応力は1/√2となる。反対にラバー厚さが半分の時、内部応力は√2倍になる。
同一ラバーを用いた場合のラバー厚さと歪エネルギーの関係を下記に参考として示した。
摩擦力は荷重を N,比例定数を μ とすればF= μNである。球がラバーに加わる力は、ラバーと球の接触面積をA、応力をσとするとF = μσAとなる。
その結果、ラバーが厚いと球に回転がかかり難く、ラバーが薄いと球に回転がかかり易い。
後で回転の合成で球の飛びを制御することを述べるが、薄いラバーは回転をかけ易いということは、薄いラバーは、大きい方向変化をコントロールし易いのだ。
では、何故、厚いラバーを使う必要があるのか。厚いラバーは薄いラバーよりも歪み限度が大きい、これは厚いラバーにはより大きいエネルギーを蓄えることができる。
遠くへ飛ばすことができるのだ。
後陣で打つことに向いているが前陣で打つことには向いていない。反対に薄いラバーは前陣で打つことにはむいているが後陣で向いていないのだ。
相手のラバーの種類や厚さを知ることは大事なことだ。相手から繰り出される球種を予想できるから、対策を立て易くなる。
たまに、特厚ラバーを前陣で使っている人もいる。
卓球台から飛び出し易いのだから、飛び出し易い球を相手に出せば有利に戦えるはずだ。
メーカーのホームページを見るとラバーの性能を速度と摩擦とで示した相関図が掲載されている。
メーカーの図では横軸を摩擦、縦軸を速度とするものが多いが、私は横軸を速度とし縦軸を摩擦とした。
球の飛びをシミレーションするのは、こちらの方がイメージし易いでしょう。
Fig-1.3.1
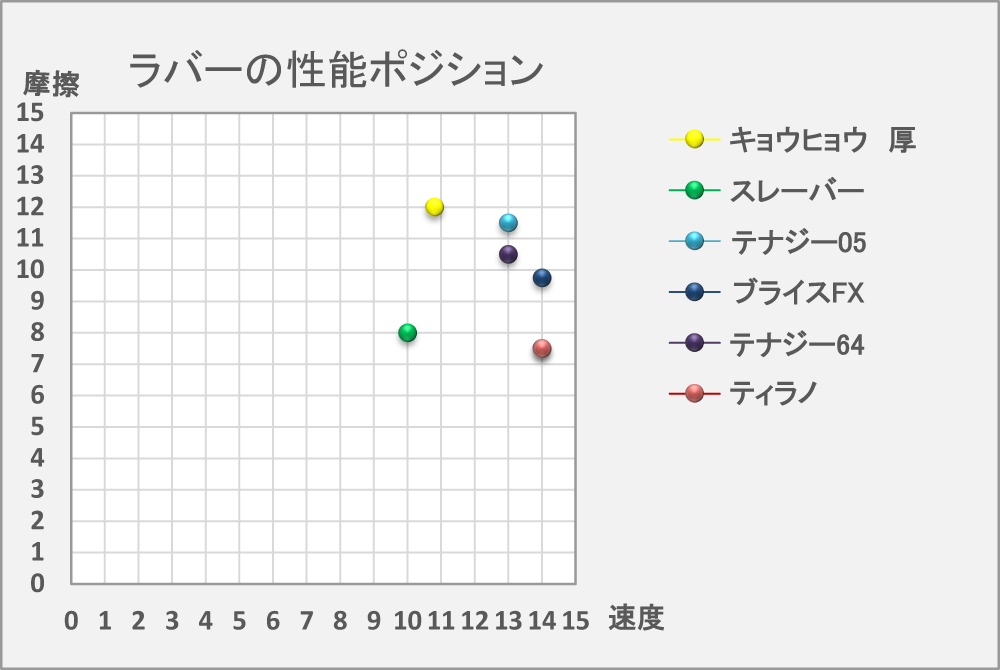
上記ラバーの速度と摩擦をパラメータとしてシミュレーションしたのが次の図だ。
球はラバーから離れるとマグナス効果で軌道が決まってしまう。
キョウヒョウでネットに引っ掛かる傾向の人は、テナジーを使えば良いということになる。
ティラノでは飛びすぎるかもしれない。スレーバーでは打ちやすい球になってしまうだろう。
Fig-1.3.2
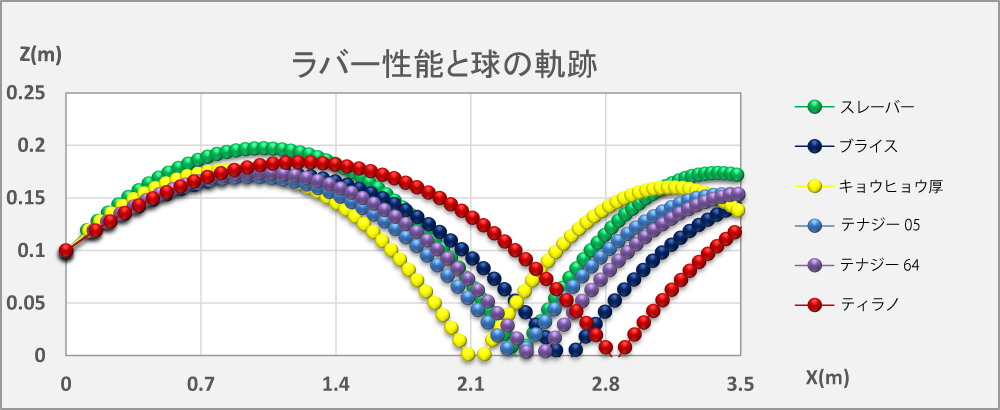
もどる
<参考>
ラバー厚さと歪エネルギーの関係
固定された断面積がA0、初期厚さl0のラバーに、垂直方向に圧力Pを作用させた結果、作用方向にdλだけ縮んだとすると。
圧力Pのした仕事dWは、
dW = P dλ
W = ∫0λ P dλ
σ = Eε
σ = P/A0
ε = λ/l0
P = EA0λ/l0
W = ∫0λ P dλ = ∫0λ E A0/l0 λdl
= E/2 A0/l0 λ2
基準のラバー厚さの添え字を1とし、基準の2倍厚のラバーの添え字を2とし、
W1 = W2の時のラバー内部応力を比較してみよう。
λ12/l1 = λ22/l2
λ2 = √(l2/l1) λ1
= √(2l1/l1) λ1 = √2 λ1
よって
σ1 = Eλ1/l1
σ2 = Eλ2/l2 = E√2 λ1/ 2l1 = (E/√2) λ1/l1 = (1/√2) σ1
即ち、ラバー厚さが2倍の時、内部応力は1/√2となる。反対にラバー厚さが半分の時、内部応力は√2倍になる。
ラバーの厚さがn倍の時
σn = (1/√n) σ1
となる。
もどる

