1.5 球のはね方
力学に「運動量保存の法則」というのがある。卓球に当てはめて簡単に言うと、運動の形態は変わっても、その合計は一定に保たれるというものだ。 この法則によると、球の回転は、球の運動に変わっても、回転の運動量と飛びの運動量の合計は一定だ。
この節では、裏ラバーの張ってある静止しているラケットに、 無回転の球、ドライブしている球、下回転している球が当たった時の球のはね方を示した。
1.5.1 無回転のはね方
下の図は、静止しているラケットに回転していない球が当たったときの球のはね方を示す。 球が下から上がってくるのは、卓球台でバンドした球をイメージしている。
Fig-1.5.1
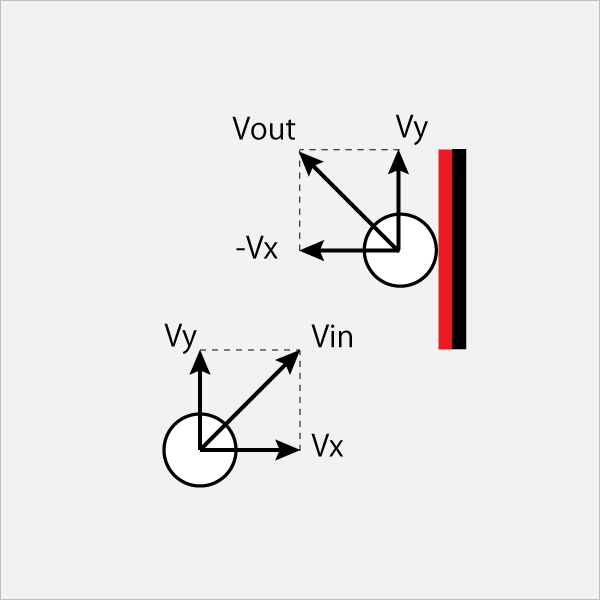
Vinで飛んできた球は、 ラケットとぶつかると水平速度-VxとVinの垂直速度Vyとの合成速度となってVoutの方向に飛んでいく。 Vyは方向を変えるものがないが、Vxはラケットで方向がかわるのだ。
1.5.2 ドライブ回転のはね方
下の図は、上回転(ドライブ回転)している球が当たったときの球のはね方を示す。
Fig-1.5.2
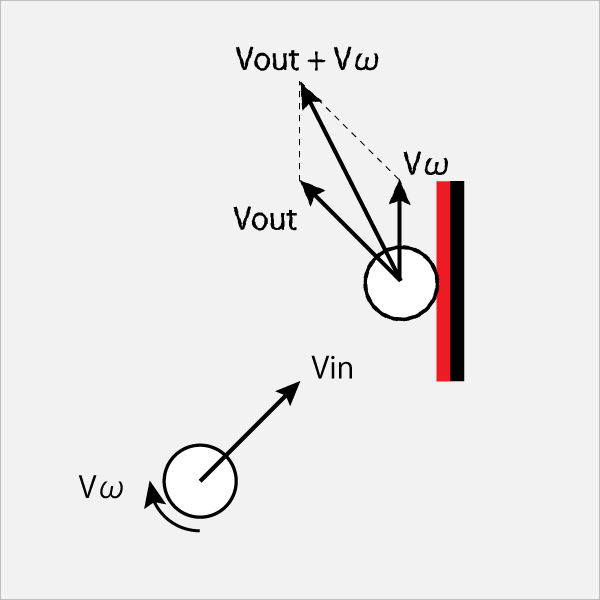
Vinで飛んできた球は、
ラケットとぶつかると水平速度-VxとVinの垂直速度Vyとの合成速度となってVoutの方向に飛んでいく。ここまでは無回転と変わらない。
しかし球はωの回転しているので、ラケットから回転反力を受ける。その結果、球の回転ωは垂直速度Vωに変換される。
したがって、合成速度Vout+Vωとなりラケットから飛んでいく。
1.5.3 下回転のはね方
下の図は、下回転している球が当たったときの球のはね方を示す。
Fig-1.5.3
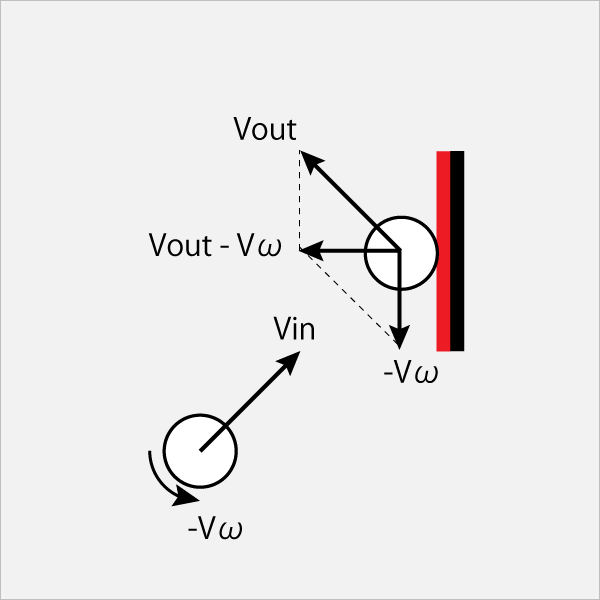
Vinで飛んできた球は、
ラケットとぶつかると水平速度-VxとVinの垂直速度Vyとの合成速度となってVoutの方向に飛んでいく。ここまでは無回転と変わらない。
しかし球は-ωの回転をしているので、ラケットから回転反力を受ける。その結果、球の回転ω垂直速度-Vωに変換される。
したがって、合成速度Vout-Vωとなりラケットから飛んでいく。
1.5.4 下回転を利用して戻す
下の図は、下回転をラケットを水平にして持ち上げた時の球のはね方を示す。
Fig-1.5.4
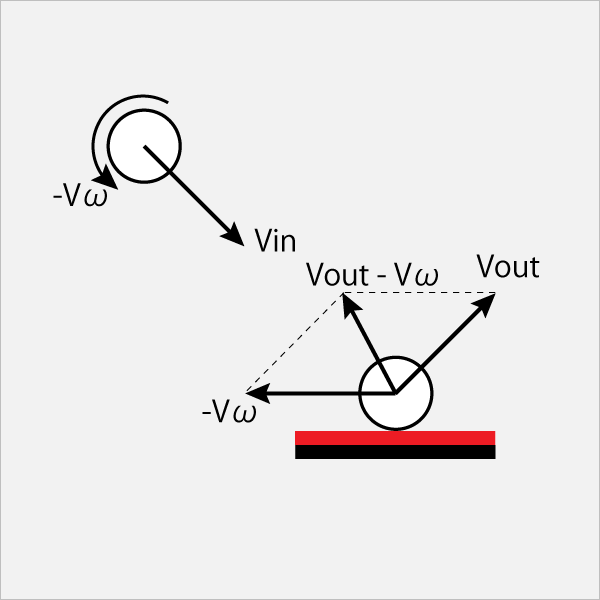
ラケットを水平にして上方にシッカリと支えると、合成速度はVout-Vωとなり、回転を止めて球の来た方へ戻っていく。 私はこの振り方を「シャクリ」と呼んでいる。試合の様々な場面で使う。