2.3 横回転を下回転で返球
横回転のサービスをドライブで返球を続けると、相手も慣れてくる。 そこで、この振り方を混ぜてやれば相手は迷う。 今までコートに入っていた下切りに対する角度打ちで打ったとしても、間違いなくネットにかかる。 正に直角の下回転なのだから。
球に、ラケットでこの回転を加えれればどんな打ち方でも良い。 横回転には上軸回転(カーブ回転)と下軸回転(シュート回転)の二種類がある。回転方向が逆なので、 返球方法も逆の回転を与えることになる。
2.3.1 カーブ回転をカット回転で返球
相手からの球の回転は同じではあるが、配給によってバック側かフォア側で受けることになる。 ラケットでの球への回転の与え方は、いずれも球の下半球にシュート回転を与えるのだ。 この振り方をシュート・カットと呼ぶことにしよう。
(A)バック側のカーブ回転をカット
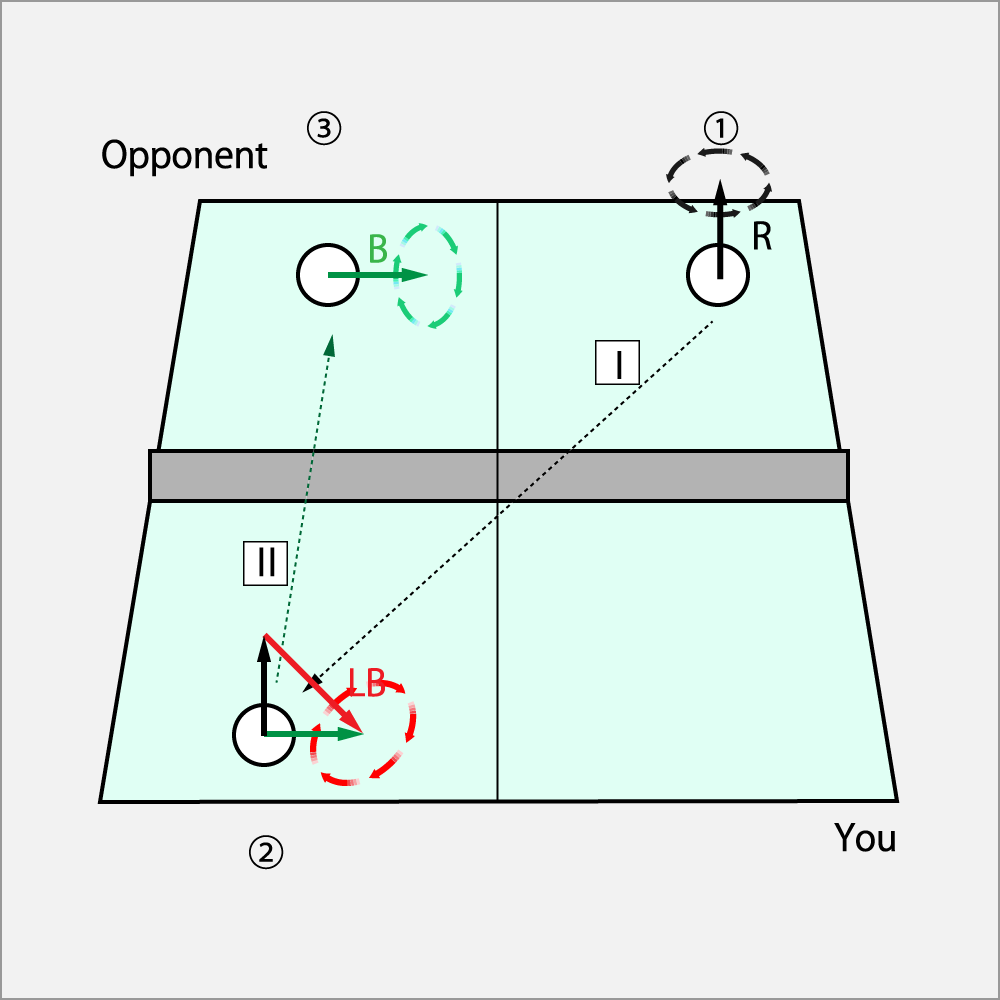
では、打球の順番を追って見てみよう。
① 相手がカーブ(R)でバック側にサーブした。
② 自分のコートに入ったⅠの回転に②のシュート・カット(LB)を加える。
③ 相手のコートにはカット(B)となって返球される。
方程式は以下の通りとなる。
カット = カーブ + シュート・カット
英語の頭文字で表記すると,
B = R + LB
振り方は3.4.1節 「横回転(カーブ回転)のカット返球技術:バックの振り」を参考にして欲しい。
(B)フォア側のカーブ回転をカット
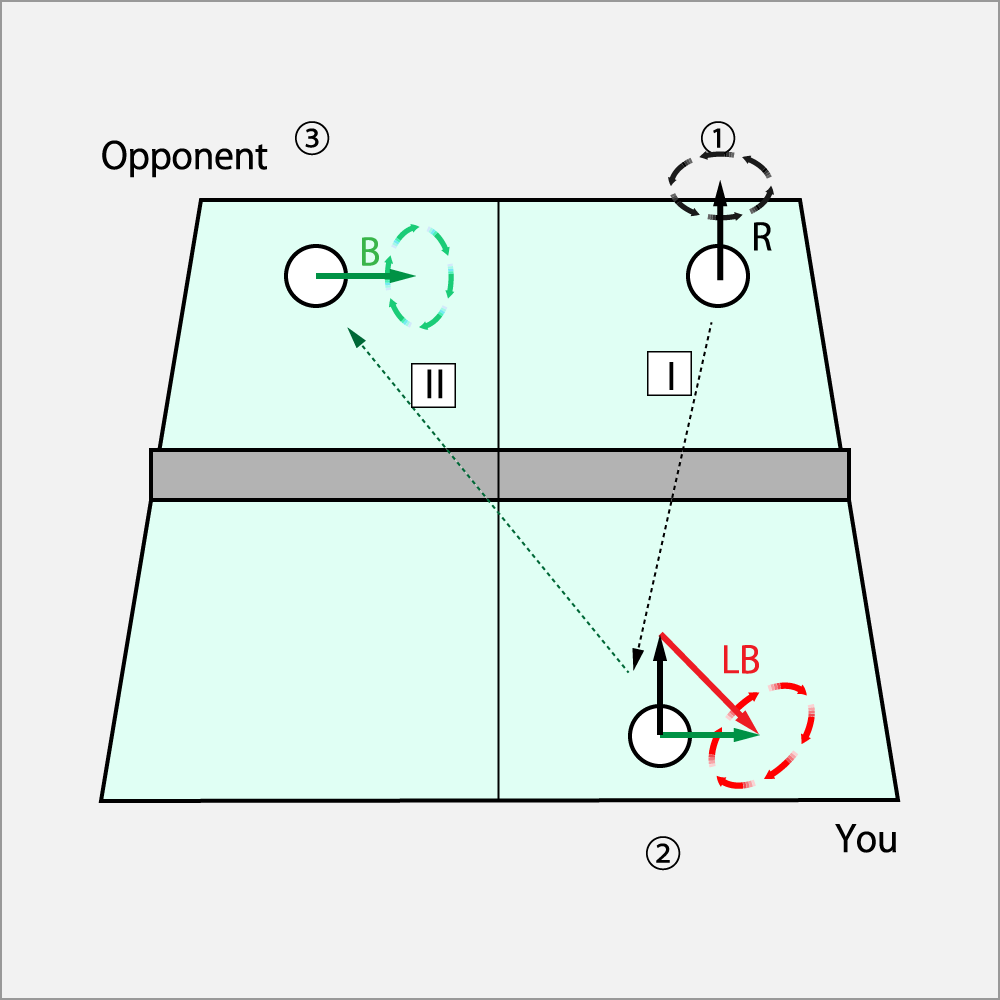
① 相手がΘカーブ(R)でフォア側にサーブした。
② 自分のコートに入ったⅠの回転にシュート・カット(LB)を加える。
③ 相手のコートにはⅡのカット(B)で返球される。
方程式は以下の通りとなる。
カット = カーブ + シュート・カット
英語の頭文字で表記すると,
B = R + LB
振り方は3.4.2節 「横回転(カーブ回転)のカット返球技術:フォアの振り」を参考にして欲しい。
2.3.2 シュート回転をカット回転で返球
相手からの球の回転は同じではあるが、配給によってバック側かフォア側で受けることになる。 ラケットでの球への回転の与え方は、いずれも球の下半球にカーブ回転を与えるのだ。 この振り方をカーブ・カットと呼ぶことにしよう。
(A)バック側のシュート回転をカット
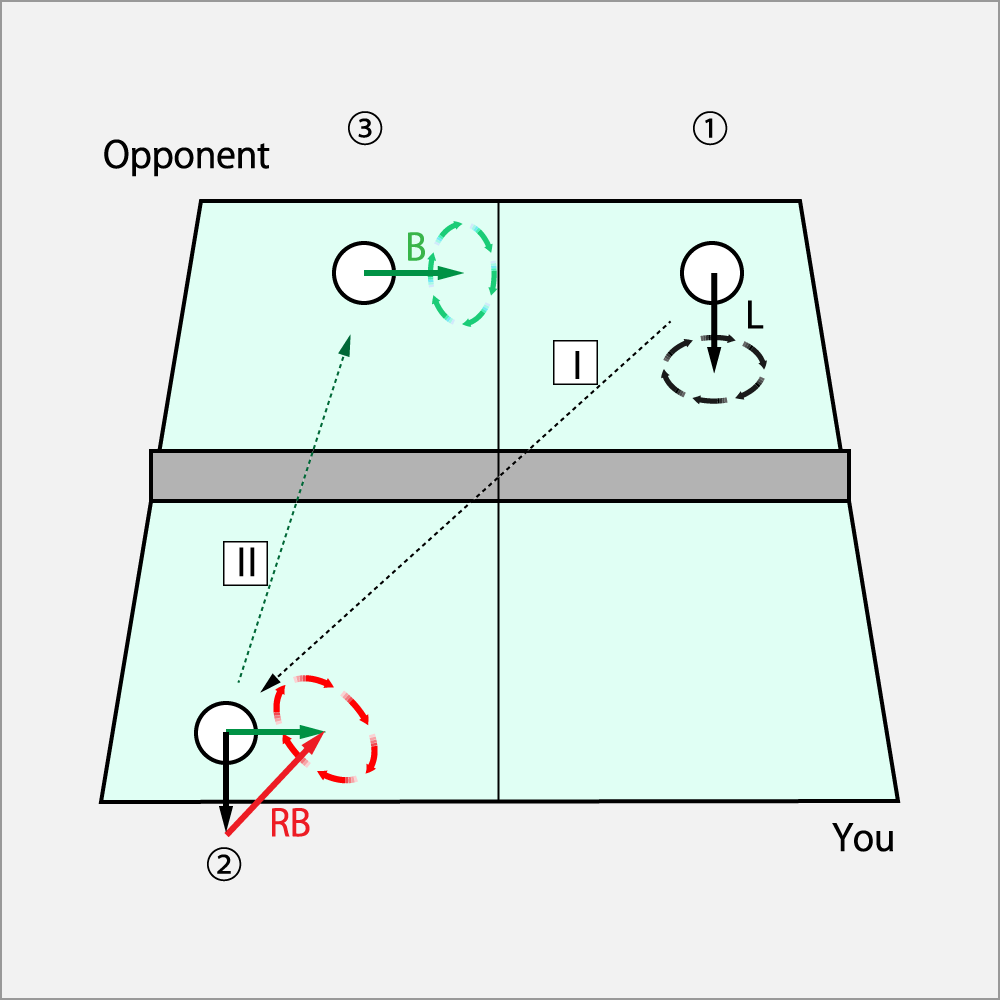
① 相手がシュート(L)でバック側にサーブした。
② 自分のコートに入ったⅠの回転にカーブ・カット(RB)を加える。
③ 相手のコートにはⅡのカット(B)となって返球される。
方程式は以下の通りとなる。
カット = シュート + カーブ・カット
英語の頭文字で表記すると,
B = L + RB
振り方は3.5.1節 横回転(シュート回転)のカット返球技術:バックの振りを参考にして欲しい。
(B)フォア側のシュート回転をカット
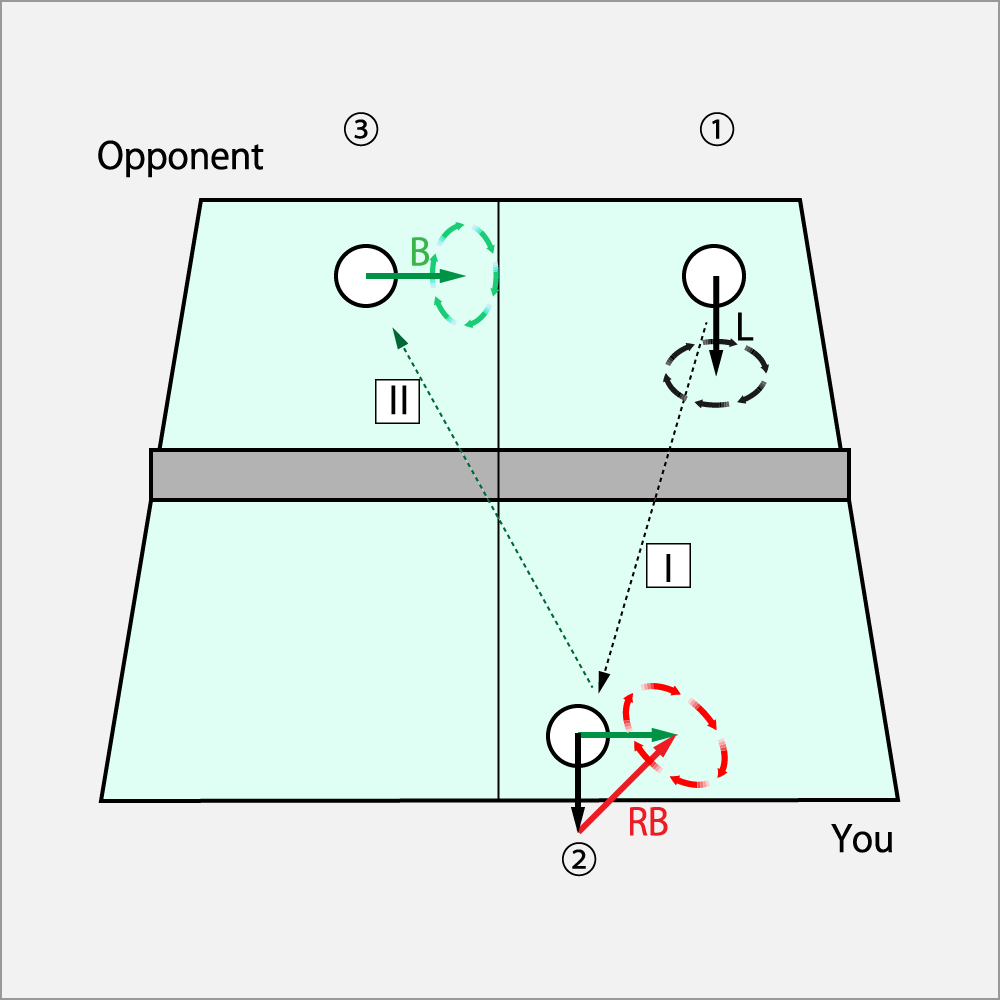
① 相手がシュート(L)でフォア側にサーブした。
② 自分のコートに入ったⅠの回転にカーブ・カット(RB)の回転を加える。
③ 相手のコートにはⅡのカット(B)となって返球される。
方程式は以下の通りとなる。
カット = シュート + カーブ・カット
英語の頭文字で表記すると,
B = L + RB
振り方は3.5.2 横回転(シュート回転)のカット返球技術:フォアの振りを参考にして欲しい。
2.3.3 横回転をカットで返球の法則
前述2.3.1では、Θカーブをシュート・カットで受けると、
Θカーブとシュートが相殺して、カットだけが残るのだ。
前述2.3.2では、Θシュートをカーブ・カットで受けると、
Θシュートとカーブが相殺して、カットだけが残るのだ。
したがって、以下の法則が成り立つ。
<横回転をカットで返球の法則>
横回転をカットで返すには、相手からくる横回転に対抗する側の下半球を前方に擦る。