2.7 攻撃のブロック
3球目攻撃の後は、ブロックだね。
ここでは、相手の強いドライブにどう対処したら良いかを話すことにしょう。
君は相手の強いドライブに対して、それ以上の回転を掛けなければならないと思っていないだろうか。
相手の回転が勝っていれば球は、ラバーの反力で上方向に遠くに飛んで行ってしまう。
それ以上の回転を掛けようとして強く振れば更に遠くに飛んで行ってしまう。
ブロックには、二つの考え方があり、いずれも大切だ。
一つは、相手のドライブの反力を使って返球する方法。
もう一つは、相手のドライブの回転方向を変えてしまう方向だ。
2.7.1 相手のドライブの反力を使って返球する方法
第1部 基礎の「打球点の角運動量」で示した図をもう一度見てみよう。
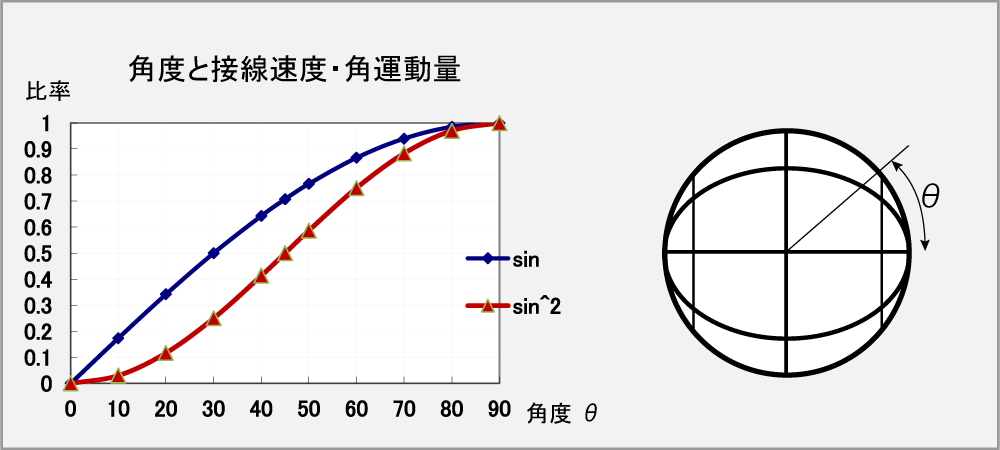
相手の強いドライブも角度を極方向に移動させれば反力はsin^2カーブで小さくなるのだった。 角度45°の所で当てれば反力は0.5となり、球がネットから飛び出すことはなくなる。
注意すべき点
- 反力はラケットに平行に働くのでラケットを前方に倒し球の左肩を当てる。
- 球がラケットに当たる瞬間に、ラケットをシッカリと固定し、前方には押し出さないこと。
- 打球点角度を相手の回転スピードに合わせて調整する事。
- 返球の安定感を増す為に懐付近でとらえる為に、打球点を予測し左右にすばやく移動する。
この方法の良いところはラケットを振らないので、相手の速い球に対して振り遅れが無くなく追従し易いところだ。
2.7.2 相手のドライブの回転方向を変えてしまう方法
回転の合成を知っていれば、別な対策も講じられる。この方法にはカーブ/シュート回転と、Hコーク/Fコークを与える方法がある。
2.7.2.1 ドライブをカーブ/シュート回転でブロック
ラケットをワイパーの様に横に振る。即ち球の前面を左右を擦るのだ。
そうすれば、回転の軸は上下方向に傾き、上方向の力が少なくなる。
前方向に振るわけでは無いので台から飛び出ることはない。
実際にやってみると、台の奥深くカウンターになることが分かるだろう。
振り方には、球にカーブを与える振りと、シュートを与える振りがある。
(A) ドライブをカーブ回転でブロック
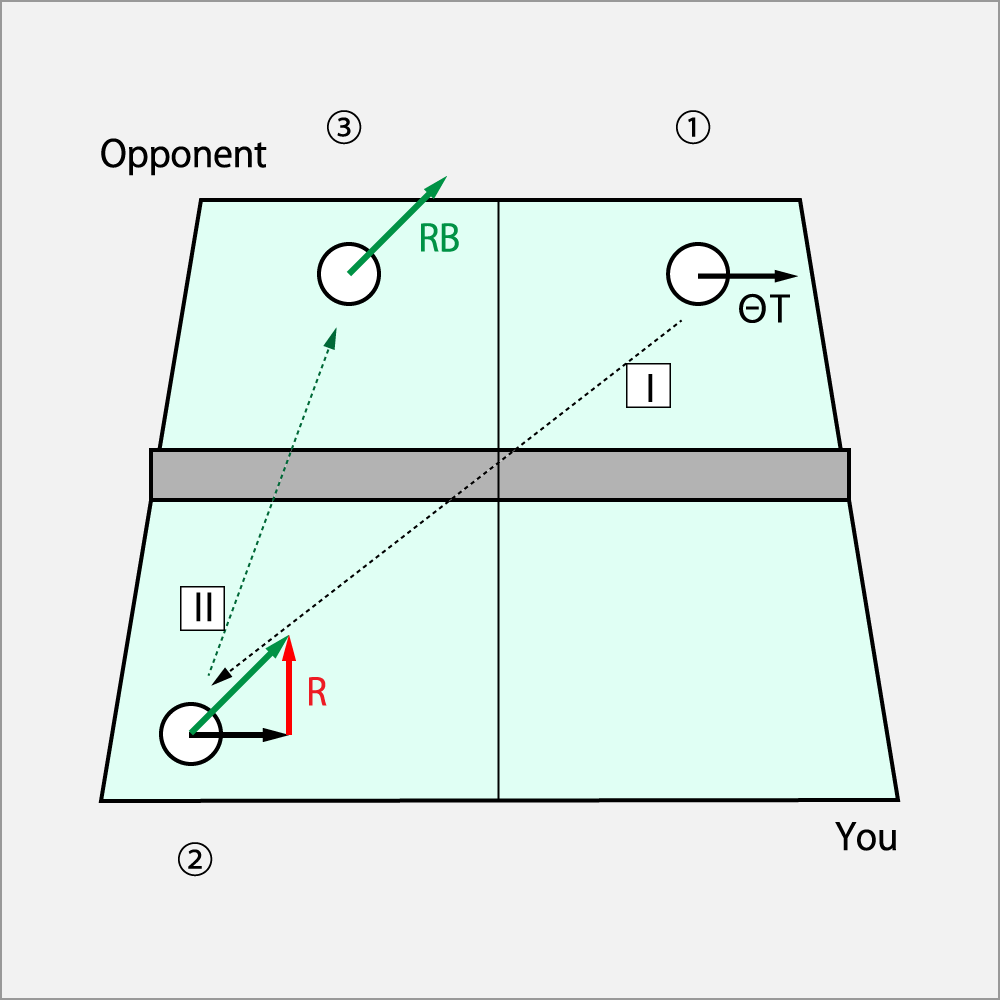
① 相手がⅠの強いΘドライブ(ΘT)を返球した。
② 自分のコートに入ったⅠの回転にカーブ(R)でブロックした。
③ 相手のコートにはⅡのカーブ・カット(RT)で送球された。
方程式は以下の通りとなる。
カーブ・カット = Θドライブ + カーブ
英語の頭文字で表記すると、
RB = ΘT + R
(B) ドライブをシュート回転でブロック
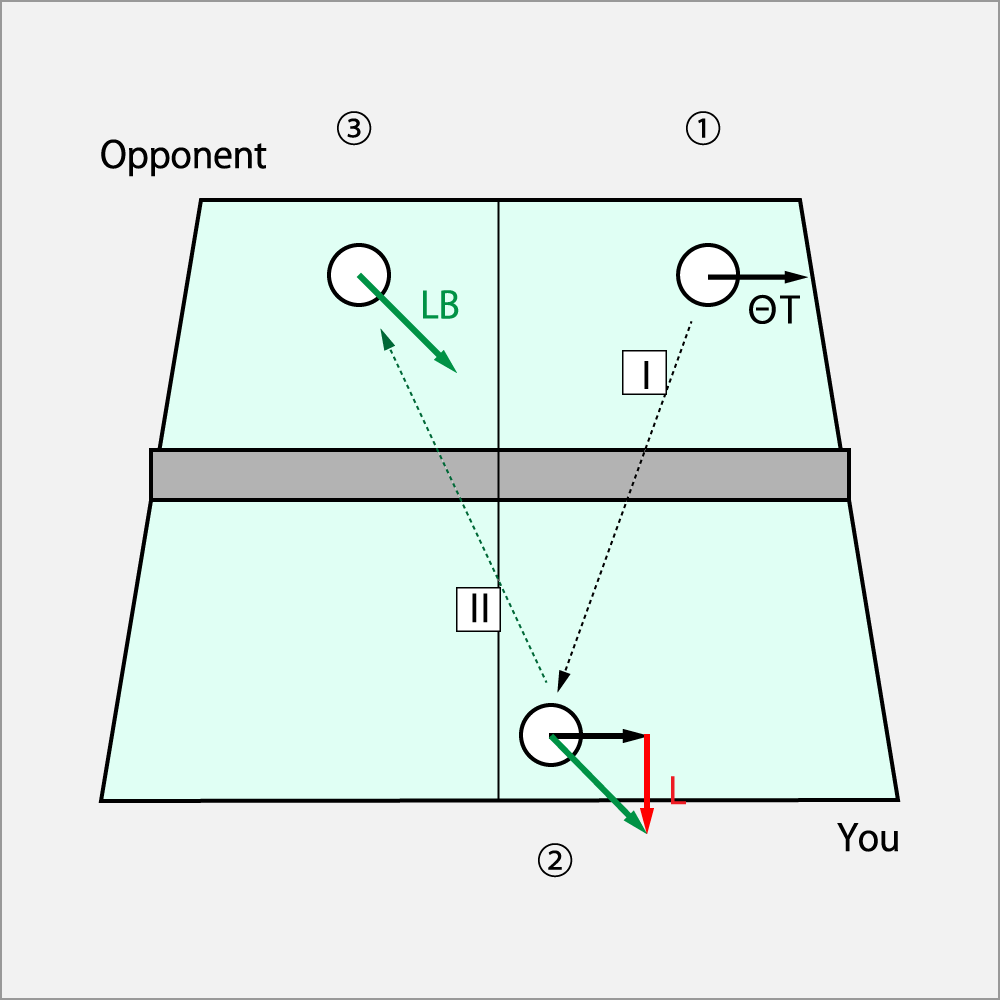
① 相手がⅠの強いΘドライブ(ΘT)を返球した。
② 自分のコートに入ったⅠの回転に②のシュート(L)でブロックした。
③ 相手のコートにⅡのシュート・カット(LB)で送球された。
方程式は以下の通りとなる。
シュート・カット = Θドライブ + シュート
英語の頭文字で表記すると、
LB = ΘT + L
2.7.2.2 ドライブをHコーク/Fコーク回転でブロック
ラケットを水平にして球の上側を横に擦るのだ。
そうすれば、回転の軸は左右方向に傾き、上方向の力が少なくなる。
前方向に振るわけでは無いので台から飛び出ることはない。
実際にやってみると、台の奥深くカウンターになることが分かります。
振り方には、球にHコークを与える振りと、Fコークを与える振りがある。
(A) ドライブをHコーク回転でブロック
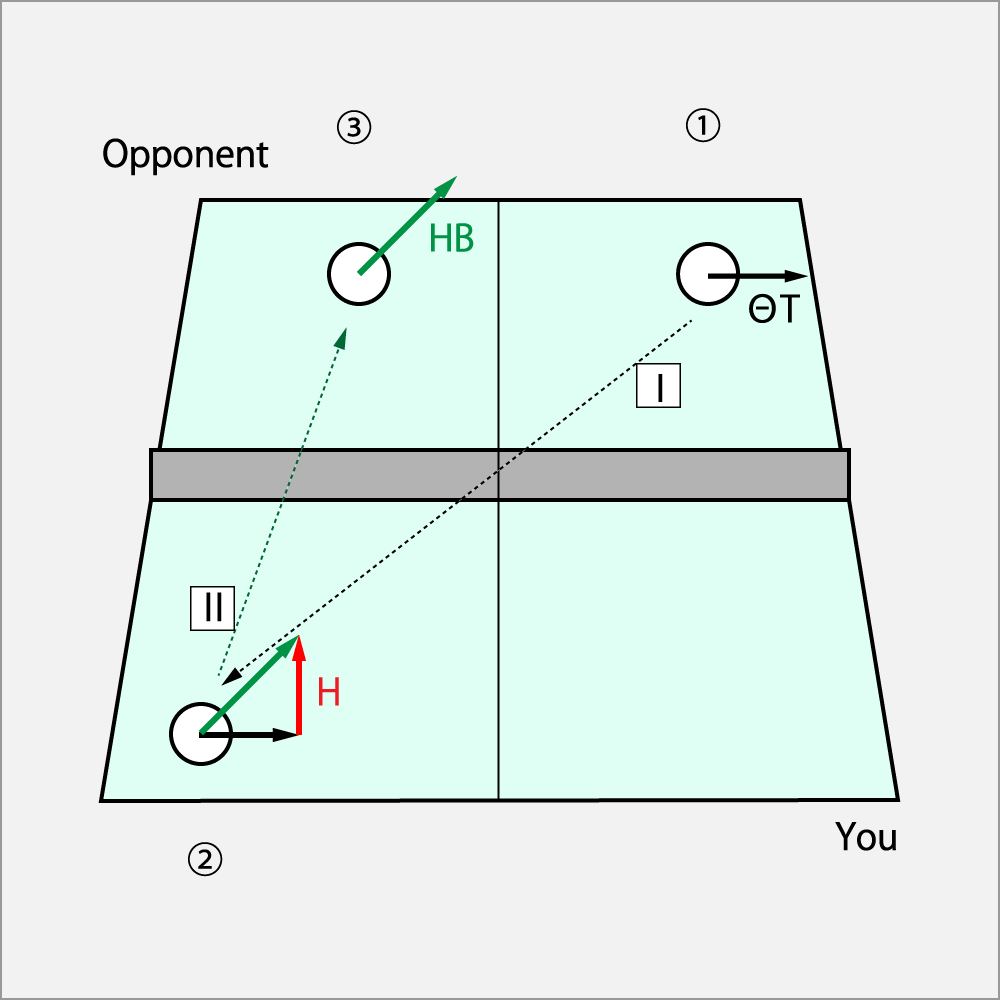
① 相手がⅠの強いΘドライブ(ΘT)を返球した。
② 自分のコートに入ったⅠの回転にHコーク(H)でブロックした。
③ 相手のコートにⅡのHコーク・カット(HB)で送球された。
方程式は以下の通りとなる。
Hコーク・カット = Θドライブ + Hコーク
(B) ドライブをFコーク回転でブロック
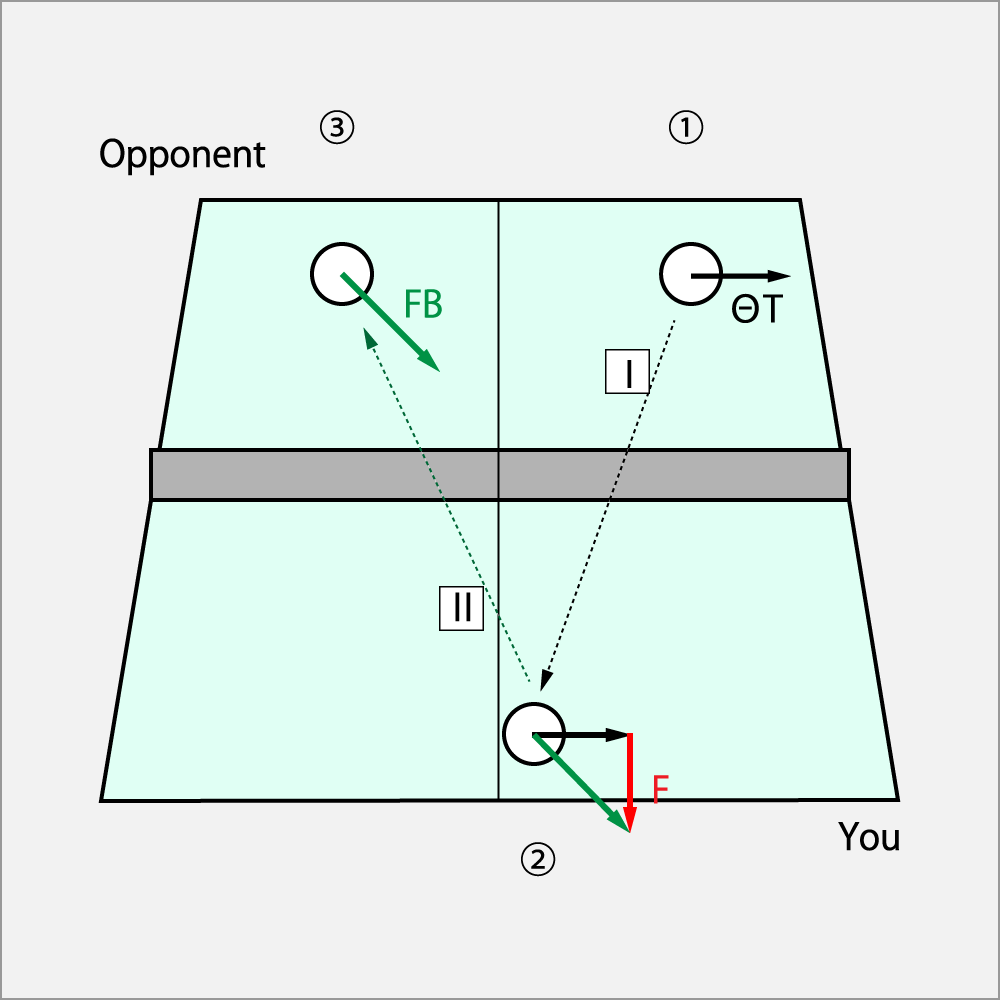
① 相手がⅠの強いΘドライブを返球した。
② 自分のコートに入ったⅠの回転にFコークでブロックした。
③ 相手のコートにⅡのFコーク・カットで返球された。
方程式は以下の通りとなる。
Fコーク・カット = Θドライブ + Fコーク
英語の頭文字で表記すると、
FB = ΘT + F