2.9 3球目攻撃
既に、回転の合成によるレシーブを学んできた。自分のサーブに対して、
相手が普通に返した場合の球の回転は、回転の合成から予想がつくから、3球目をドライブで攻めるとして、
どう打てば良いのかがここのテーマとなる。
ここでの技術を習得すると、3球目攻撃ってこんなに簡単だったのか。
今まで、3球目攻撃が入らなかったのは球の回転を知らなかったからだと気付かされるはずだ。
更に、「3球目攻撃の法則」を理解すると、様々の攻撃が出来るようになり卓球の質が格段に上がることだろう。
2.9.1 カーブ回転でサーブ、ドライブでレシーブさせて、シュート・ドライブで3球目攻撃
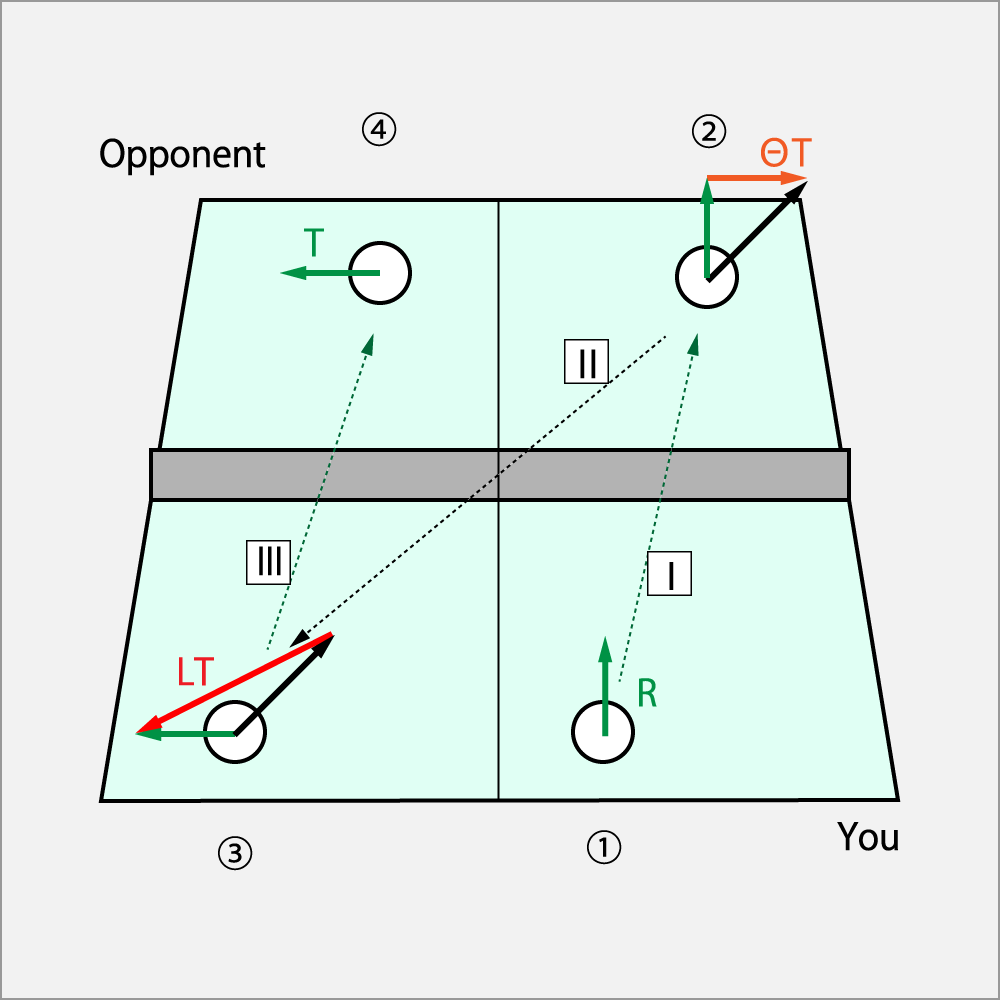
では、打球の順番を追って見てみよう。
① 自分がⅠのカーブ(R)でサーブを相手のバック側深くに出す。
② 相手はⅠの回転をΘドライブ(T)で受ける。その結果Ⅱのカーブ・カット(RB)で返球される。
③ 返球されたⅡのカーブ・カット(RB)に対し、シュート・ドライブ(LT)を加えて、Ⅲのドライブ(T)として送球し④となる。
ベクトル図で分かる通り、④で決める為には、③で加えるシュート・ドライブは強く与えることが求められる。
方程式は以下の通りとなる。Θドライブ回転はカット回転なので、
カーブ・カット = カーブ + Θドライブ
ドライブ = カーブ・カット + シュート・ドライブ
英語の頭文字で表記すると、
RB = R + ΘT
T = RB + LT (但し、LT>LB)
話を要約すると、カーブでサーブし、シュート・ドライブで仕留める。
バック側に返球された図となっているが、フォワー側に返球されても、同様の回転を球に加えれば良い。
2.9.2 シュート回転でサーブ、ドライブでレシーブさせて、カーブ・ドライブで3球目攻撃
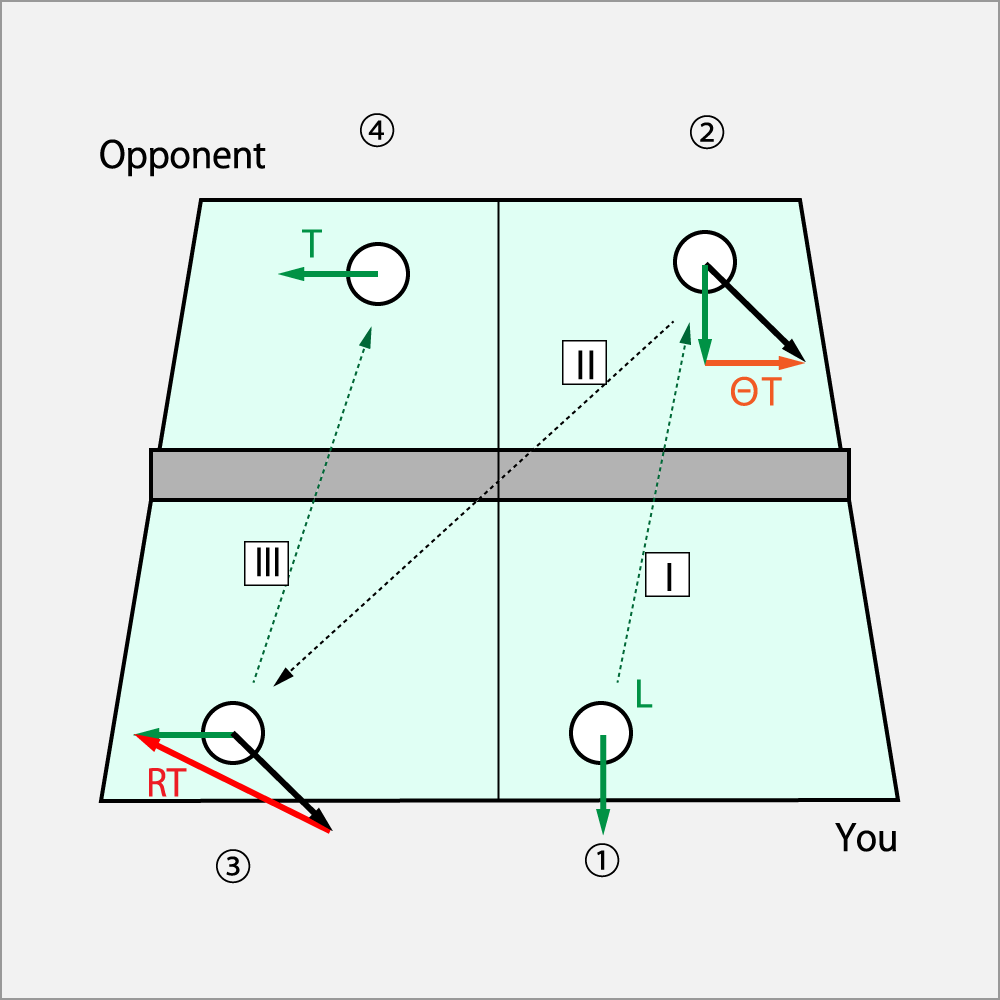
① 自分がⅠのシュート(L)でサーブを相手のバック側深くに出す。
② 相手はⅠの回転をΘドライブ(ΘT)で受ける。その結果Ⅱのシュート・カット(LB)で返球される。
③ 返球されたⅡのシュート・カット(LB)に対し、カーブ・ドライブ(RT)を加えて、Ⅲのドライブ(T)として送球する。
ベクトル図で分かる通り、④で決める為には、③で加えるシュート・ドライブは強く与えることが求められる。
方程式は以下の通りとなる。Θドライブはカットなので、
シュート・カット = シュート + Θドライブ
ドライブ = シュート・カット + カーブ・ドライブ
英語の頭文字で表記すると、
LB = L + ΘT
T = LB + LT (但し、LT>LB)
話を要約すると、シュート回転でサーブし、カーブ・ドライブで仕留める。
バック側に返球された図となっているが、フォワー側に返球されても、同様の回転を球に加えれば良い。
どう打てば良いかは自分で考えて見て欲しい。考える癖をつけることが大切だ。
2.9.3 3球目攻撃の第一法則
相手のサーブがΘドライブあるいはブロックて受けることが予想出来れば、容易に3球目攻撃で打ち抜くことが出来る。
前述の2.9.1では、①カーブのサービスを②Θドライブで受けさせ④シュート・ドライブで3球目攻撃
前述の2.9.2では、①シュートのサービスを②Θドライブで受けさせ④カーブ・ドライブで3球目攻撃
これらのことから、自分のサーブ回転は、相手のレシーブの後でも残り、それを手掛かりに三球目攻撃を考えることが出来る。
だから、次の組み合わせも成り立つ。
カーブ = カーブ・ドライブ + Θドライブ
ドライブ = カーブ+ シュート・ドライブ
あるいは、
シュート = シュート・ドライブ + Θドライブ
ドライブ = シュート+ カーブ・ドライブ
したがって、以下の法則が成り立つ。
<3球目攻撃の第一法則>
相手がサーブをドライブあるいはブロックで受けるのであれば、横回転ドライブでサーブし、3球目攻撃では相殺する横回転ドライブを加えればドライブとして相手に戻る。
要は、横回転を巻き戻す様に3球目に横回転ドライブを加えれば良いのだ。
2.9.4 Hコーク・カット回転を左ショートフォアに出して、ツッツキでレシーブさせ、Fコーク・ドライブで3球目攻撃
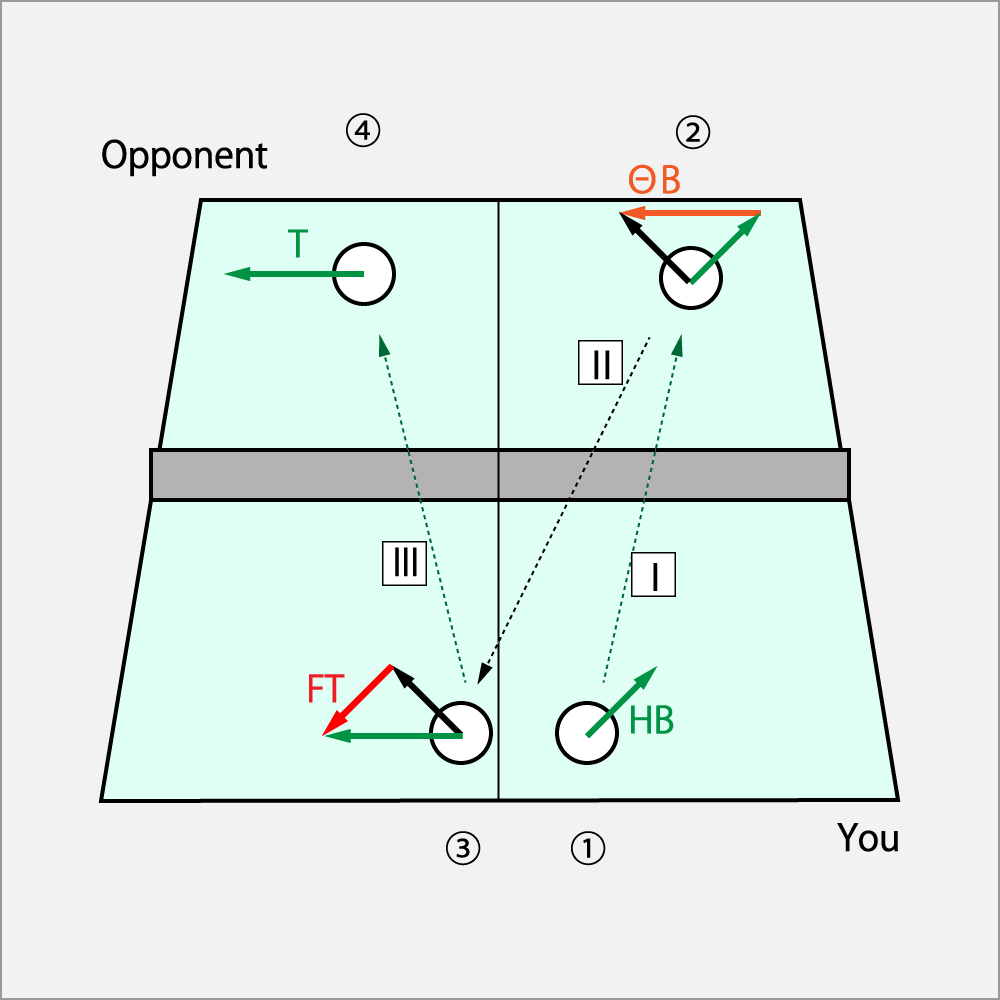
① 自分がⅠのHコーク・カット(HB)でサーブを相手のバックへ出す。
② 相手はⅠの回転をΘカット(ΘB)で受ける。その結果ⅡのHコーク・ドライブ(HT)で返球される。
③ 返球されたⅡのHコーク・ドライブ(HT)に対し、Fコーク・ドライブ(FT)を加えて、Ⅲのドライブ(T)として送球する。
方程式は以下の通りとなる。Θカットはドライブなので、
Hコーク・ドライブ = Hコーク・カット + Θカット
ドライブ = Hコーク・ドライブ + Fコーク・ドライブ
話を要約すると、Hコーク・カット(HB)でサーブし、Fコーク・ドライブ(FT)で仕留める。
左サイドに向かってFコーク回転させる振りは、頭で分かっていても体はその様には動いてくれない。
最初はなかなか出来ないかもしれない。その内に、コツをつかめるようになる。
これが出来るようになると回転の合成が本当に理解出来るようになる。
2.9.5 Fコーク・カット回転を右ショートフォアに出して、ツッツキでレシーブさせ、Hコーク・ドライブで3球目攻撃
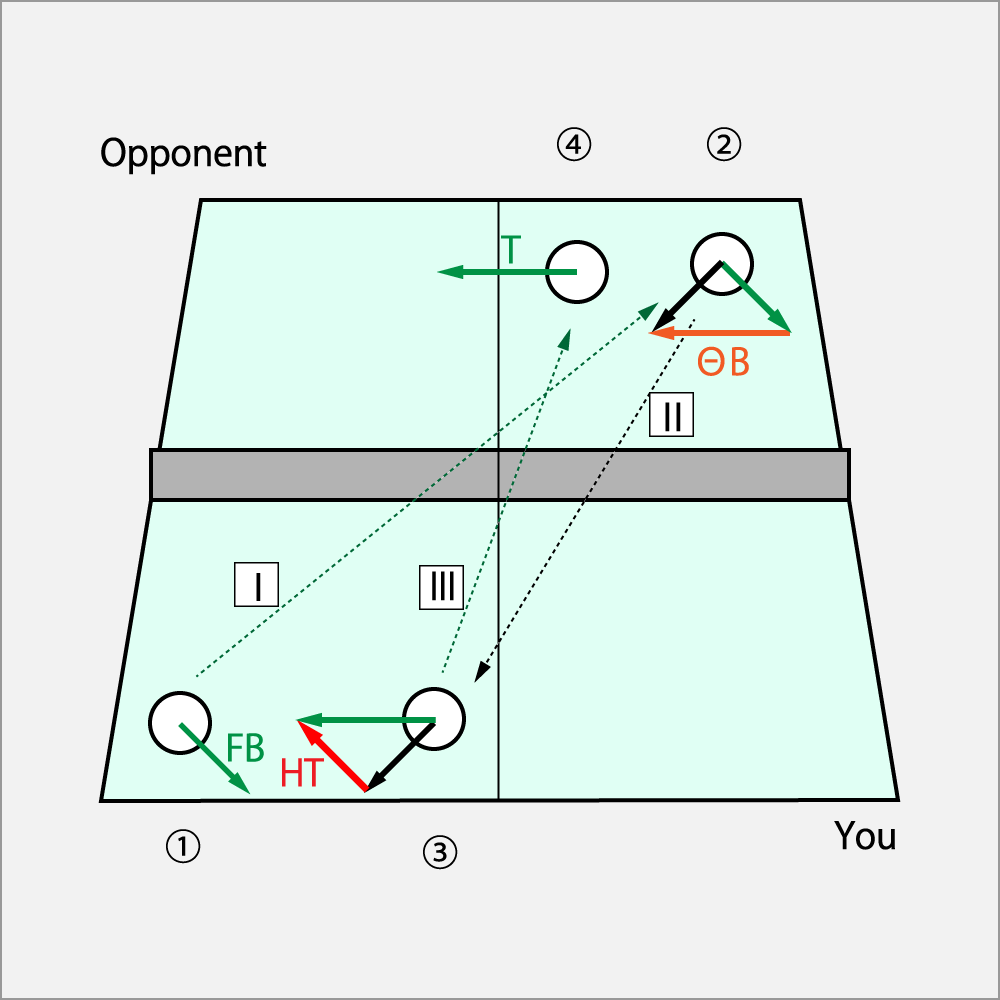
① 自分がⅠのFコーク・カット(FB)でサーブを相手のバックへ出す。
② 相手はⅠの回転をΘカット(B)で受ける。その結果ⅡのFコーク・ドライブ(FT)で返球される。
③ 返球されたⅡのFコーク・ドライブ(FT)に対し、Hコーク・ドライブ(HT)を加えて、Ⅲのドライブ(T)として送球する。
方程式は以下の通りとなる。Θカットはドライブなので、
Fコーク・ドライブ = Fコーク・カット + Θカット
ドライブ = Fコーク・ドライブ + Hコーク・ドライブ
話を要約すると、Fコーク・カットでサーブし、Hコーク・ドライブで仕留める。
右サイドに向かってHコークさせる振りは、頭で分かっていても体はその様には動いてくれない。
最初はなかなか出来ないかもしれない。その内に、コツをつかめるようになる。
また、新しい振りを覚えたことになる。
2.9.6 3球目攻撃の第二法則
相手がサーブをΘカットで受けることが予測出来れば、あるいはΘカットで受けるように仕向ければ、
実は様々な3球目攻撃を作ることが出来る。
前述の2.9.4では、①Hコーク・カットのサービスを②Θカットで受けさせ③Fコーク・ドライブで3球目攻撃
前述の2.9.5では、①Fコーク・カットのサービスを②Θカットで受けさせ③Hコーク・ドライブで3球目攻撃
こられのことから分かることだが、自分が与える①と③の回転は、実は、①の回転を③の回転で相殺しているのだ。
そしてその結果として、相手が加えた②Θカットの回転が④ドライブとして残っていることが分かる。
だから、次の組合せも成り立つ。
カーブ・ドライブ = カーブ・カット + Θカット
ドライブ = カーブ・ドライブ + シュート・ドライブ
あるいは、
シュート・ドライブ = シュート・カット + Θカット
ドライブ = シュート・ドライブ + カーブ・ドライブ
あるいは、
カーブ・ドライブ = カーブ + Θカット
ドライブ = カーブ・ドライブ + シュート
あるいは、
シュート・ドライブ = シュート + Θカット
ドライブ = シュート・ドライブ + カーブ
したがって、以下の法則が成り立つ。
<3球目攻撃の第二法則>
相手がサーブをカットで受けるのであれば、自分からのサーブ回転を3球目攻撃で相殺する回転を加えれば、どんな回転でもドライブとして相手に戻る。
要は、サーブの回転を巻き戻す様に3球目で回転を加えれば良いのだ。