1.11 方程式からみた球とラケットの回転速度
1.6 節「球とラケットの回転速度」の関係について、この節では角運動方程式から、少し厳密に表現している。
微分方程式が出てくるが、各ケースについて、その結果を説明しているで、図と併せてみれば理解できると思う。
ニュートンの運動の第一法則を回転運動に広げて述べると、
回転を変化させるとき、そこには力のモーメントが働いている。
力のモーメントが働いてないと、現状の回転を続けるか、無回転であれば無回転であり続ける。
そのことが、球の角運動方程式で表現されているのだ。
座標と拘束条件
- ここで扱う回転は一次元座標とする。
- ラケットのラバーの摩擦が大きく滑りが無いものとする。
- ボールに比べラケットの質量は十分大きく、ボールはラケットを動かすことが出来ない。
球の角運動方程式
卓球ボールの角運動方程式は
Iω’(t) = N
tで積分すると、
Iω(t) = N(t-t0) + Iω0
以降で扱う変数は、I:慣性モーメント、ω:角速度、ω0:初期角速度、N:加える力のモーメント、t:時間 t0:基準時間、R:反力による角運動量、v0:初期飛行速度、v:飛行速度、r:半径、m:質量
1.11.1 初速ω0より速い角速度ω(t)で順回転方向へ擦った場合
ラケットによる擦りの条件
ω(t) > ω0
加えた角運動量
N(t-t0) = Iω(t) - Iω0
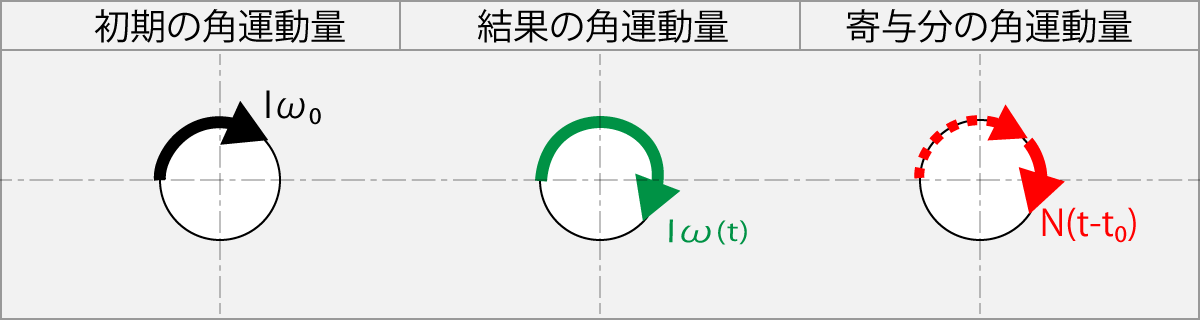
この式は、球の初期角速度ω0より速い角速度ω(t)のラケットで順回転方向へ擦った場合、
初期回転速度ω0からω(t)の差分に対して、トルクN(t-t0)が働いたことを示している。
以下の図はその関係を示しており、左に初期の角運動量、中央には結果の角運動量、右に寄与した角運動量を示す。
Fig-1.11.1
1.11.2 初速ω0と同じ速さの角速度ω(t)で順回転方向へ擦った場合
ラケットによる擦りの条件
ω(t) = ω0
加えた角運動量
N(t-t0) = Iω(t) - Iω0
=0
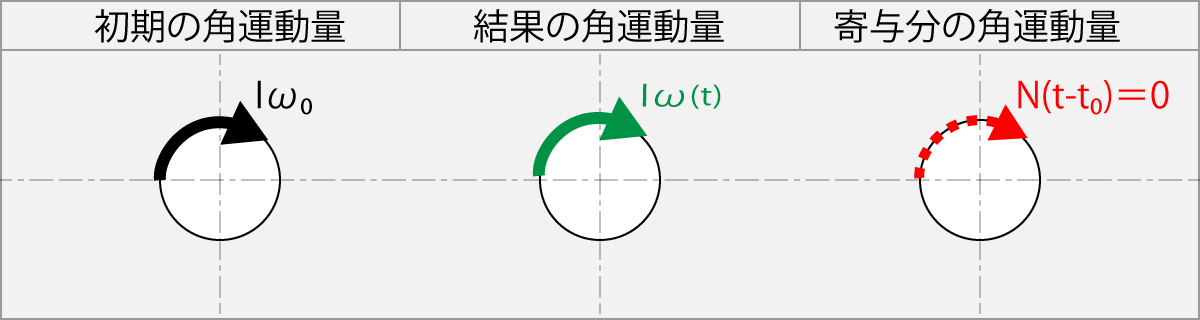
この式は、球の初期角速度ω0と同じ速さの角速度ω(t)のラケットで順回転方向へ擦った場合には、トルクが寄与しないことを示している。
Fig-1.11.2
1.11.3 初速ω0より遅い角速度ω(t)で順回転方向へ擦った場合
ラケットによる擦りの条件
|-ω(t)| < ω0
ラバーからの反作用による飛行速度へ変換
R =Iω(t) - Iω0
m(v0-v(t))r = Iω(t)-Iω0
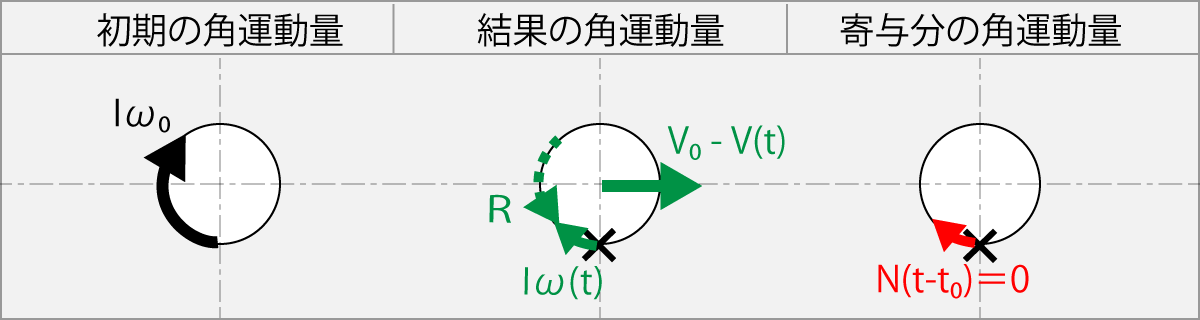
この式は、球の初期角速度ω0より遅い角速度ω(t)のラケットで順回転方向へ擦った場合、 もし、ラバーが滑るものであれば、角運動量の差Iω0 -Iω(t)は球に残る。
しかし、ラバーに滑りが無いとω0とは逆の方向にブレーキRがかかる。 球の軸は固定されていないので球がラケットを回転させることが出来ない、だから慣性力により回転の角運動量の差分が球の飛行速度v0-v(t)に変わる。
実際のラバーはこれらの中間にある。
図の×はボール上のラケットの擦る場所を示している。
ラバーが滑らない時
Fig-1.11.3
1.11.4 初速ω0を回転を与えないでラケットに当てた場合
ラケットによる擦りの条件
ω(t) = 0
ラバーからの反作用による飛行速度へ変換
R = Iω(t) - Iω0
R =0 - Iω0
m v0 r =-Iω0
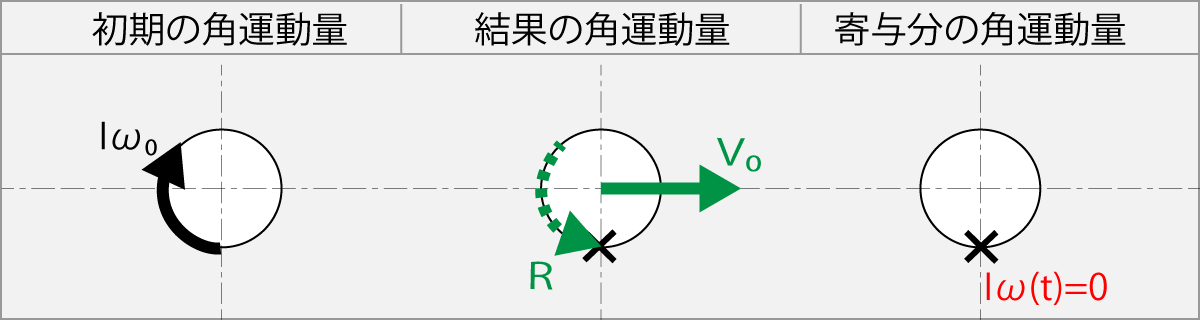
この式は、ボールに回転を与えないでラケットを当てた場合を示している。
球の軸は固定されていないので、球がラケットを回転させることが出来ないので、ラバーからの反作用により初期の運動量が慣性力により回転から球の飛行に変わる。 ×点でラケットに擦るものとしている。
図の×はボール上のラケットの擦る場所を示している。
Fig-1.11.4
1.11.5 初速ω0より遅い角速度ω(t)で逆回転方向へ擦った場合
ラケットの擦り条件
|-ω(t)| < ω0
ラバーからの反力による飛行速度への変換
Iω(t) = R + Iω0
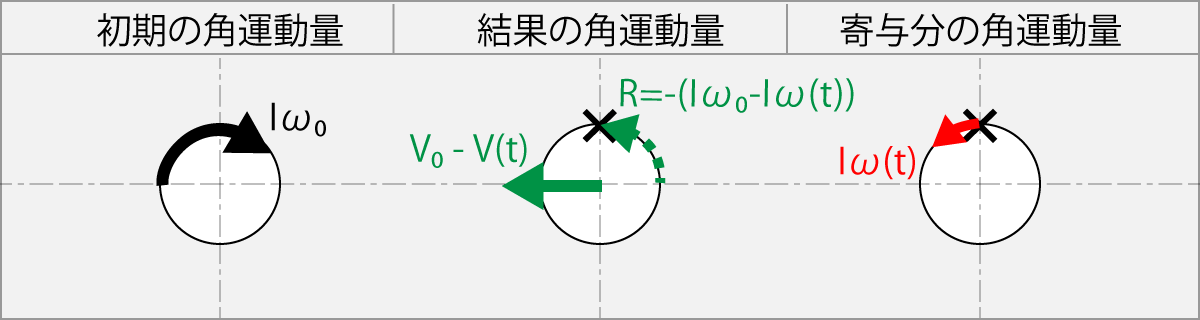
R = -(Iω0 -Iω(t))
m(v(t) - v0)r = -(Iω0 -Iω(t))
この式は、球の初期角速度ω0より遅い角速度ω(t)のラケットで逆回転方向へ擦った場合を示している。 もし、ラバーが滑るものであれば、角運動量の差Iω0 -Iω(t)は球に残る。
しかし、ラバーが滑らないのであれば、
球の軸は固定されていないので球がラケットを回転させることが出来ないので、だから慣性力により回転の角運動量の差分が球の飛行速度v(t) – v0に変わる。
実際のラバーの滑りはこれらの中間にある。
図の×はボール上のラケットの擦る場所を示している。
ラバーが滑らない時
Fig-1.11.5a
ラバーが滑る時
Fig-1.11.5b
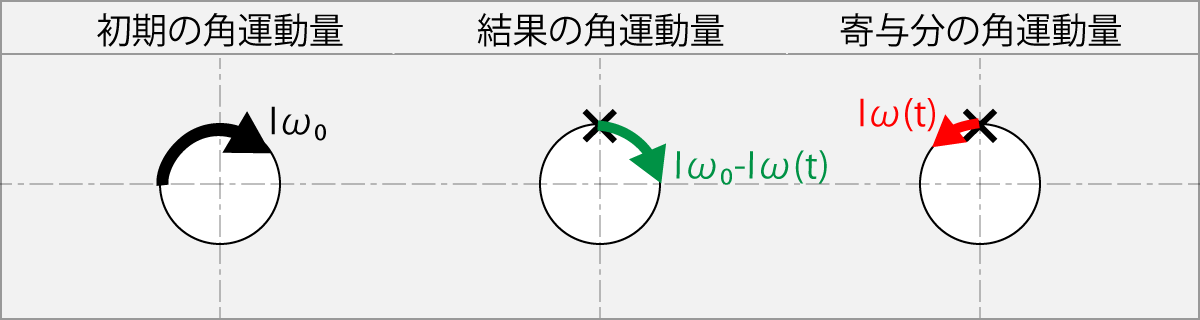
1.11.6 初速度ω0と同等な角速度ω(t)の逆回転方向へ擦った場合
ラケットの擦り条件
N(t - t0) = -Iω 0
結果の角運動量
Iω(t) = N(t-t0) + Iω0
Iω(t) = -Iω0 + Iω0
Iω(t) = 0
この式は、球の初期角速度ω0と同等な角速度ω0のラケットで逆回転方向へ擦った場合は、球は回転を止めることを示している。
Fig-1.11.6
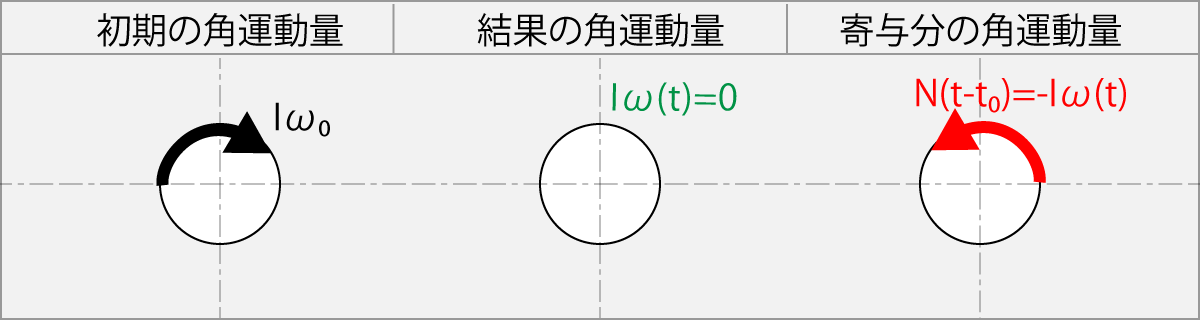
1.11.7 初速ω0より2倍速い角速度ω(t)で逆回転方向へ擦った場合
ラケットの擦り条件
N(t - t0) = -2Iω 0
結果の角運動量
Iω(t) = N(t-t0) + Iω0
Iω(t) = -2Iω0 + Iω0
Iω(t) = -Iω0
この式は、球の初期角速度ω0より2倍の角速度2ω0 のラケットで逆回転方向へ擦った場合は、球はω0と逆回転を始めることを示している。
Fig-1.11.7
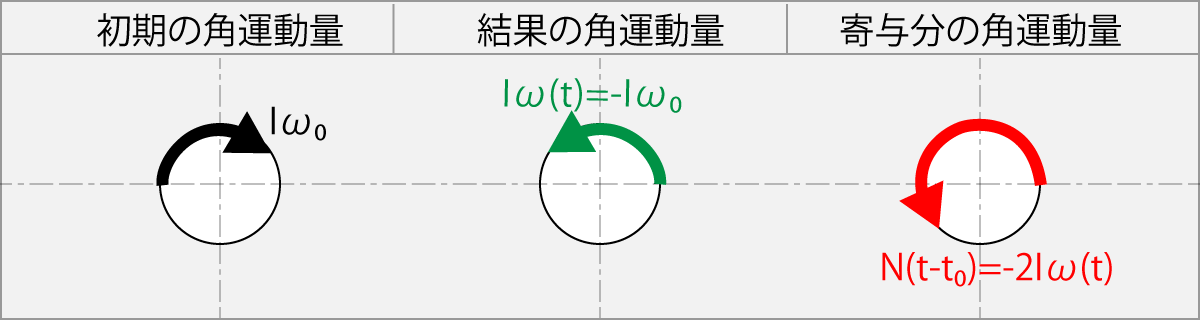
Ntを2倍にするのに、Nt=Frtであるので、Fを2倍にしてもいいし、tを2倍にしてもいい即ち接触時間を2倍にすることでもいいのだ。
1.11.8 初速角速度ω0= 0、初期速度V0に対して、水平にラケットを当てた場合
ラケットの擦り条件
ω(t) = 0
飛行停止による角運動量への変換
m(V0 - v(t)) r = Iω(t) - Iω0
m(V0 - 0) r = Iω(t) - 0
Iω(t) = mv0r
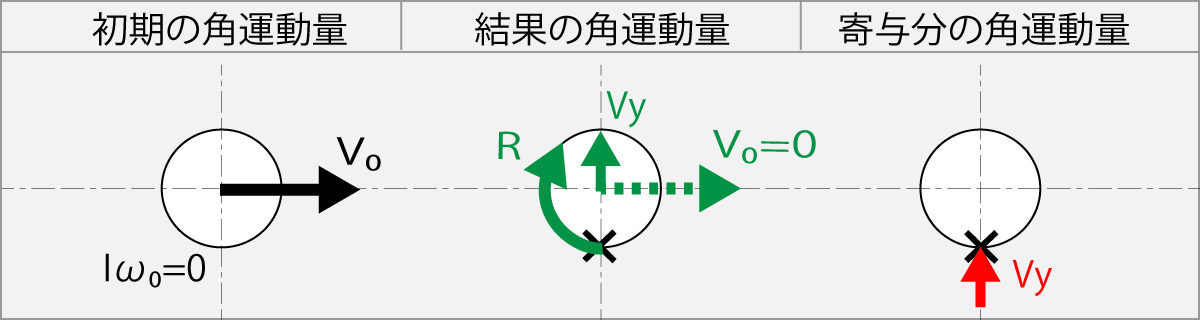
この式は、v0で飛行しているボールに摩擦係数の大きいラケットを直角方向に任意の速度Vyで当てた場合を示している。
球の飛行方向と垂直方向にラケットを移動させて接触させることにより、球はラケット面の抵抗によって飛行を止めるが、球の軸は固定されていないので、ラケットを離れた時に球の飛行は回転に変わる。この図では×点でラケット面に垂直に当てるものとしている。
Fig-1.11.8
1.11.9 順回転方向と逆回転方向の擦りの重要な違い
順回転と逆回転方向の擦りの違いは上記だけではない。重要な違いがいある。逆回転の擦りは、球とラケットのエネルギー交換は一瞬に行われるが、順回転の擦りのエネルギー交換は接触時間が長いので、 1.9.1節 「ラケットの振りと飛距離との関係」で示した様に、球を遠くへ飛ばす顕著な効果がある。これは卓球の戦術を考える上で重要なので確認しておく。