2.13. The Basics of Drive Spin Rallies

Here I will explain the basic rallies of Drive swing. I wanted to explain this section in a much earlier but I avoided. In order to explain this, it needs to explain the vector diagram which is reflected an invalid vector in spin compositions, which makes the story to be more complicated. But now the invalid vector is explained at the section 7.2 Consideration of the spin composition and vector notation. you can reffer it if you want to know.

Through the rallies in your warm-up, maybe you would have some experiences that the rallies could be stable with experienced players, but, could not be stable with inexperienced ones.
Experienced players, they know the reason from their experiences and are able to adapt opponents.
If you could understand this page you will be advantageous in a variety of rallies.

Explain why this is so.
Because the basic rally is the swings which transcribed opponent's swings into a mirror.
When opponent's swing was ΘCurve⋅Drive, and your swing is Shoot⋅Drive, the spin will become Shoot⋅Drive.
When opponent's swing was ΘShoot⋅Drive, and your swing is Curve⋅Drive, the spin will become Curve⋅Drive.
Because their spins belong to the Drive family and can get the ball into the opponent's court easily, and draws a stable orbit.

However, when your swing is Curve⋅Drive against ΘCurve⋅Drive from the opponent, the spin becomes Curve but not Curve⋅Drive you intend. The ball will fly over unexpectedly because it is Curve, and it will jump over the coat.

Notes in the under figures.

1. The number in a circle indicates the order in which the ball was hit, and the number in a square box indicates the flight order of the ball.
2. The spin vector is written on the ball.
3. The red vectors show the vector you add, and the orange vectors show the vector your opponent adds. Also, the green vectors show the spin vector of the ball heading from you to the opponent, and the black vectors show the spin vector of the ball heading from you to your opponent.
4. a dashed red vector indicate the invalid portion of a red vector, and a dashed orange vector indicate the invalid portion of a orange vector.

2.13.1. Stable Drive Spin Rallies

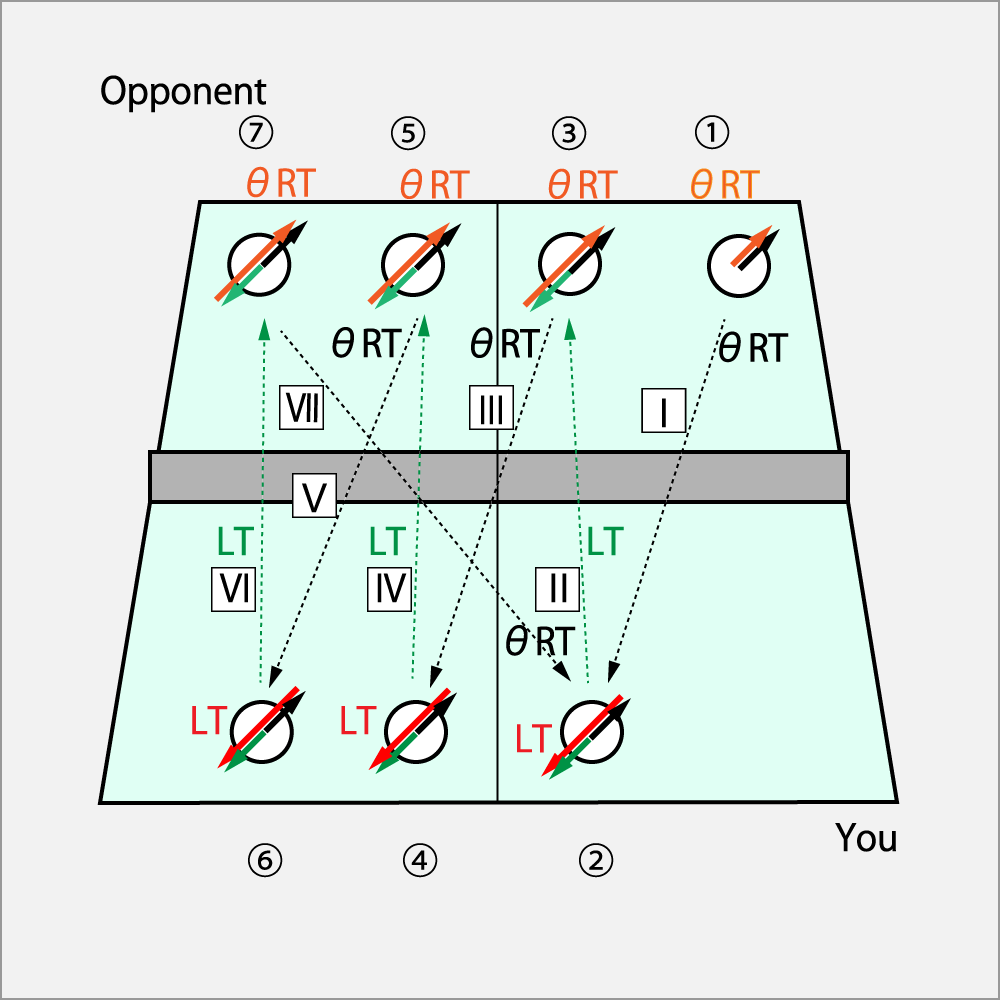
This figure shows the transition of your opponent's swing and ball rotation during a stable rally.

The opponent started the rally with the swing of ΘCurve Drive at ①, and have the same sing through ③, ⑤, ⑦.

On the other hand, you respond to the ball returned from the opponent by swinging (Shoot⋅Drive) on the mirror surface through ②, ④, ⑥.

Ⅱ, Ⅳ and Ⅵ are spins to the opponent's court.
Ⅰ, Ⅲ, Ⅴ and Ⅶ are spins coming to your own court.

The feature of this rally

1. The rotation given to you by your opponent and yourself is the same as the rotation of the flying ball. Your intention and the actual rotation of the ball is match.
2. The rotation of the ball is the rotation of the Drive system from the beginning to the end of the rally, so it remains easy to enter the court.

Return

2.13.2. Unstable Drive Spin Rallies

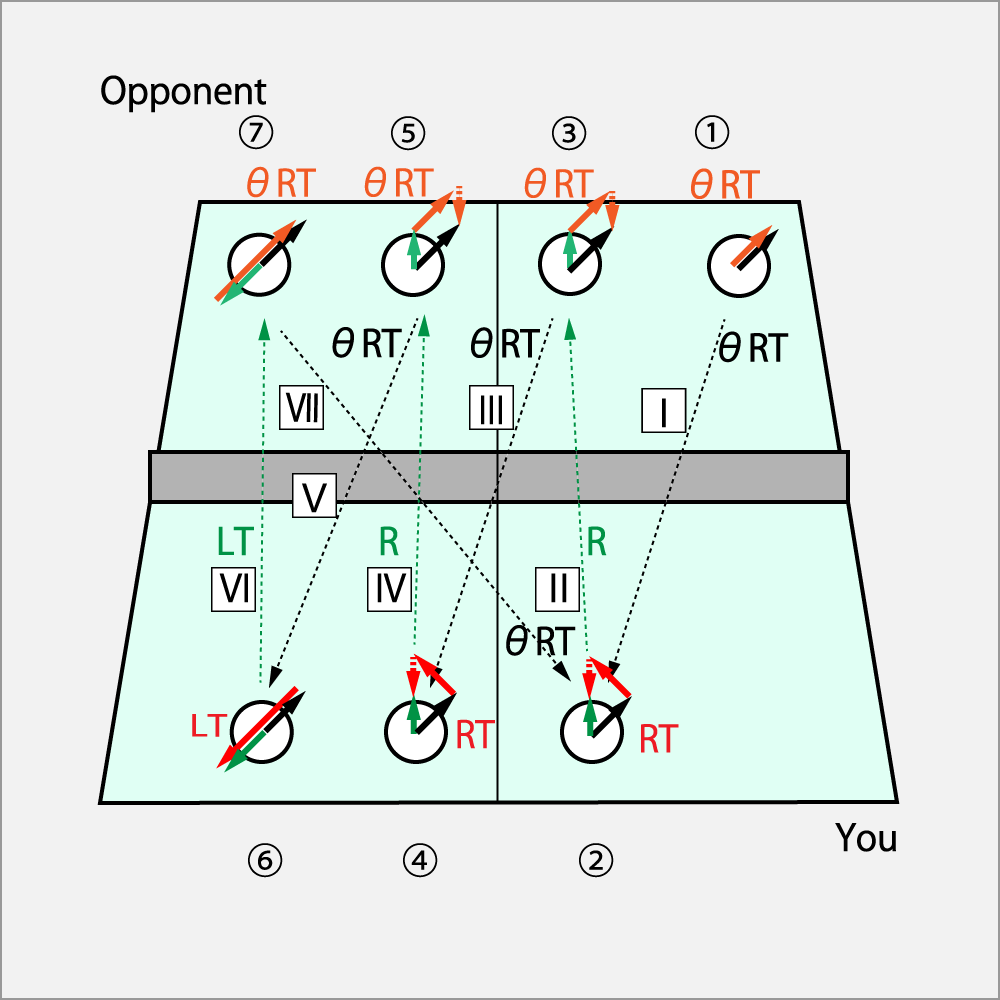
This figure shows the transition of your opponent's swing and ball rotation during an unstable rally.

The opponent started the rally with a swing of ΘCurve⋅Dirve (ΘRT) at ① and have the same swing through ③, ⑤, ⑦.

On the other hand, you respond to the return ball from the opponent with Curv⋅Dirve (RT) at ② and ④ like the opponent, and you return to a stable rally with the swing of the mirror surface: Shoot⋅Drive (LT) against the opponent's swing at ⑥.

Ⅱ, Ⅳ and Ⅵ are spins to the opponent's court.
Ⅰ, Ⅲ, Ⅴ and Ⅶ are spins coming to your own court.

The feature of this rally

1. For the opponent starting with a service, the rotation given by the swing and the direction of rotation of the ball is match.
2. For youself starting with receive, at ② and ④, the rotation of the swing is Curve⋅Drive(RT), but the spin of the ball becomes Curve(R). Your intention does not match the actual rotation of the ball.
3. On the trajectory Ⅱ and Ⅳ, the axis of the ball's rotation stands up, the flight distance is long and the giving force must be adjusted, which is unstable.
4. Therefore, your mirror swing against the opponent's swing at ⑥ is to return the flight with stability.

Return

Return