Part 4. Tactics against Various Rubberers (Service)
4.8 Backspin Service Lunch Angle
You might think that you should simply rub the bottom of the ball quickly on extension of the way you swing the drive when you give a strong back spin service.
In order to make the falling ball the fastest back spin, it is important to have a long contact time with the ball, minimize the slip between the racket and the ball, and roll with maximun acceleration.
You can make the fastest back spin service if the swing satisfies the following three conditions.
The details are explained in Section 4.9.1 and 4.9.2, if you feel it difficult, you can skip it and check Section 4.9.3.
4.8.1 Bachspin service lunch angle
I thought how to shake logically and reasonably to increase the back spin rate at making service.
It can be evaluated by the amount of energy given to the ball with the racket.
The answer is the product of the vertical stress N on the racket surface caused by the dropping ball, the friction coefficient μ and the distance of ∫vθ dt rubbed with the racket.
In the following figures, the area size of N × vθ dt indicates the amount of spin energy.
Calculation Model
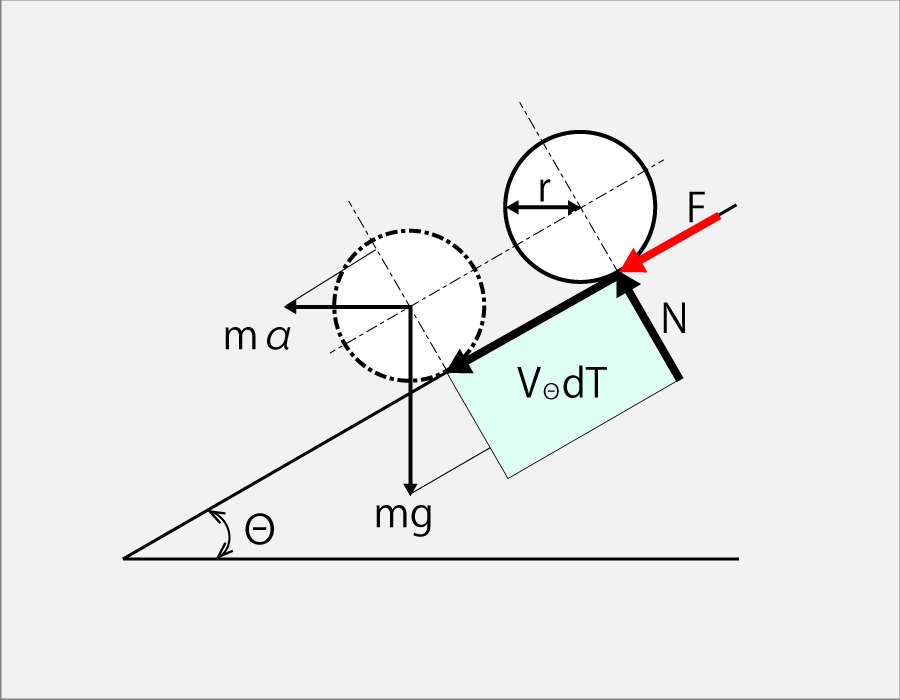
The equation of the angular momentum is
Iω’(t) = N
N = r F
F = μ m (g cos Θ + α sin Θ)
The normal stress N applied to the racket includes mg and mα.
mg is the force due to the gravity drop of the ball,
mα is defined as the horizontal force applied by the rotation of your waist,
The sum of a normal stress N is
N = r μ m ( g cos θ + α sin θ)
So, the equation of a angular momentum is,
I ω’(t) = r μ m (g cos θ + α sin θ)
When integrating with the rubbed distance,
∫I ω’r ω dt = N ∫ vθ dt
Here, μ: srip coefficient of rubber
∫I ω’ r ω dt = r μ m (g cos θ + α sin θ) ∫vθ dt
I/2 ω2 = μ m (g cos θ + α sin θ) ∫vθ dt
v θ is defined as the synchronous speed for the hitting the racket on the ball,
When a ball falling at a falling speed vg is hit by swinging down the racket at a swing speed vΘ, the size of the space in the vertical direction in which the ball is hit by the racket is proportional to the swing angle sin Θ. Of course, if the space is wide, the racket speed can be increased to make a large swing, and if the space is narrow, the racket speed can be decreased to make a small swing.
From this, it is considered that the swinging speed vΘ of the racket is obtained by multiplying the falling speed vg of the ball by k sin Θ.
The k is the ratio of the swing speed to the falling speed, and the force of the swing is adjusted.
vθ = k sin θ vg
So, if you think about k = 1 here,
I/2 ω2 = μ m (g cosθ + α sin θ) sin θ vg t
With, K = I/2 ω2
Kθ = μ m (g cosθ + α sin θ) sin θ vg t
Hereinafter, the ratio of each racket angle to the rotation speed ratio will be compared with the angle of the racket angle of 45 ° as a reference “1”. For example, at θ30 °, the speed ratio is Kθ30 ° / Kθ45 °.
(A). When only the vertical force is applied to the normal stress
The blue graph is the case where only the vertical force m g cosθ is applied on the normal stress N.
When the shaking angle is small, that is, when the racket is leveled, the vertical stress is maximized, and the synchronization speed is minimized.
Also, when the racket is vertical, the vertical stress is minimized and, conversely, the synchronization speed is maximized.
The shaking angle is θ45 ° and the amount of energy takes the maximum value, and the following graph is obtained.
I would like you to check the top professional shake. When they want to give out a strong bottom spin, they are shaking the racket about 45° downward as rubbing the ball according to "How to shaking down the racket" shown below.
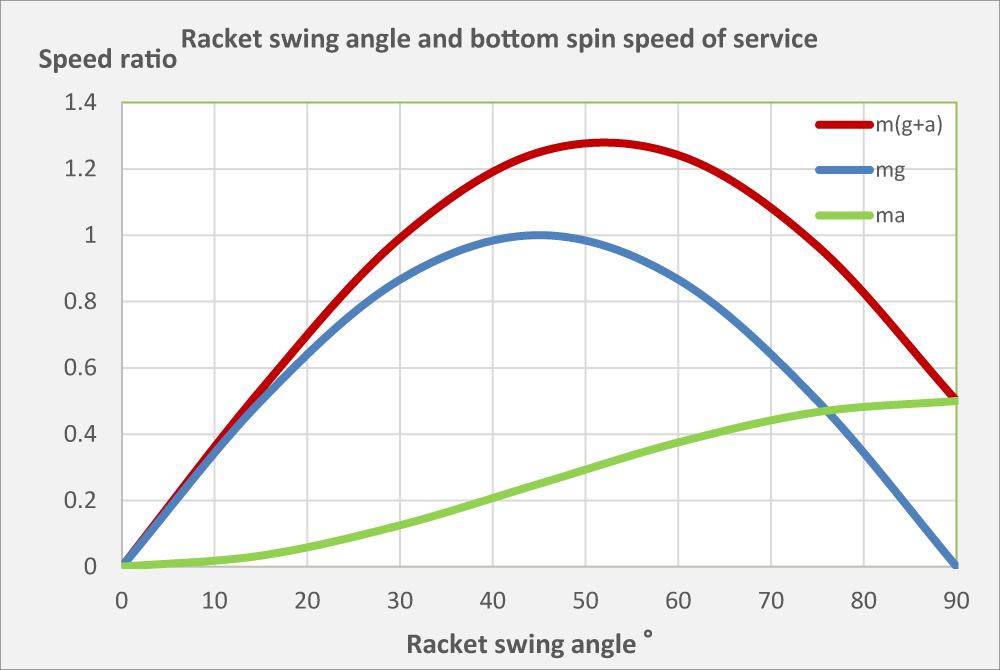
(B). When only the horizontal force is imposed to the normal stress
The yellow-green graph is the case where only the horizontal force m α sin θ is applied on the vertical stress N.
Here, the racket was set up vertically and only the waist was rotated, and α was taking 0.25g. Why is it 0.25g, because of that as rotating the waist, the racket is shaken down strongly at the 45 degrees, the distance from the beginning of the shake to the end of the shake takes 1, the distance of the rotating part of the waist is about 1/4.
(C). When the vertical and horizotal forces are imposed to the normal stress
The red graph is the case where the vertical force m g cos θ and the horizontal force m α sin θ are imposed on the normal stress N. That is, this corresponds to a case where the racket is strongly shaken down while applying pressure to the ball while rotating with the waist.
The maximum shake-down angle θ is slightly higher than 45 ° compared to when the waist is not rotated, but it takes the maximum at approximately 40-60 °, rather than simply shaking down at 45 ° It can give 1.25 times rotation.
4.8.2 Ball spin speed
The amount of energy was used to evaluate the swing angle, but what is actually needed for the serve is to increase the spin speed when the ball leaves the racket.
The equation of motion was as follows.
I ω’(t) = N
I ω’(t) = r μ m (g cos Θ + α sin Θ) vΘ'
Integrating with the rubbing time,
∫I ω' dt = r μ m (g cos Θ + α sin Θ)∫t 0 vΘ' dt
I ω = r μ m (g cos Θ + α sin Θ) (vΘ(t) - v0)
if v0 = 0 、
I ω = r μ m (g cos Θ + α sin Θ) vΘ(t)
The equation of motion says that the area obtained by adding acceleration over time is velocity. Therefore, in order to increase the spin speed, it is important to keep the acceleration vΘ' while not swinging the speed constant while rubbing the ball with the racket.
4.8.3 How to shake down the racket
When applying a strong back spin in the serve, grip the racket grip firmly so that there is no play. Keep accelerating and swinging the ball at an angle of about 45° so that the ball is rolled from the base to the tip of the grip of the racket so as to maximize the distance rubbed with the racket.Then, swing it out as if applying pressure to the ball by rotating the waist.
Grabing racket foreside

Grabing raket backside
