4.8 下回転サービスの振り抜き角度

4.8.1 振り抜き角度

下回転サービスの回転スピードと振り抜き角度との関係について考えてみた。
球がラケット面をバウンドする短い間で、 ボールに与えるエネルギー量で評価してみよう。 投げ上げたボールがラケット面に働く垂直応力Nと、摩擦係数μと、ラケットで擦った距離∫v_Θ dtの積がその答えであるから、 運動方程式をラケットで擦った距離で積分すればいい。 以下の図ではＮ v_Θ dtの面積の大きさがスピンエネルギー量を示している。

計算モデル

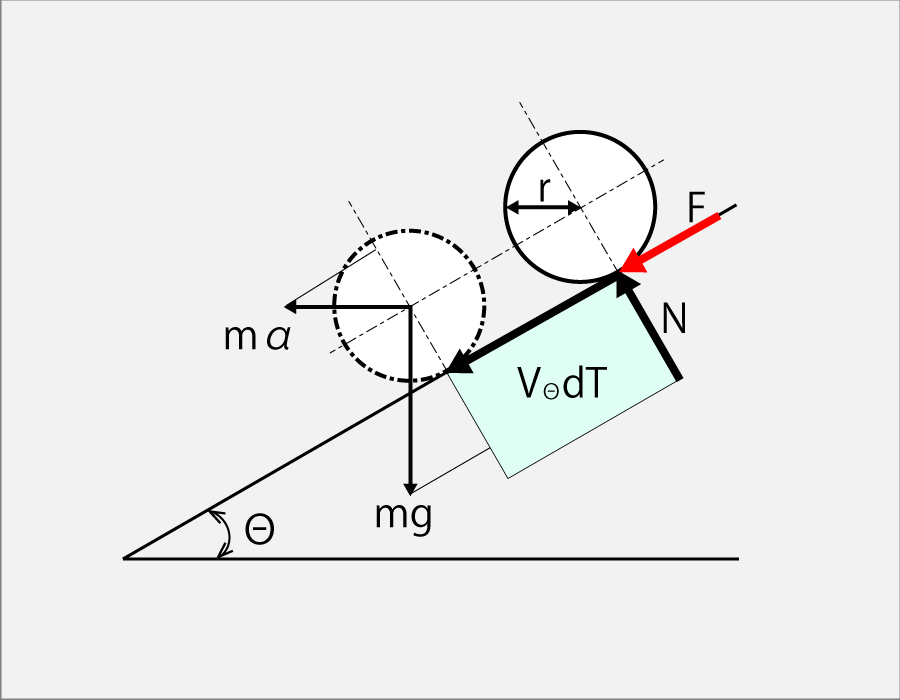
卓球ボールの角運動方程式は
I ω’(t) = N
N = r F
F = μ m (g cos Θ + α sin Θ)

ラケットに掛かる垂直応力 N には、m g と m αとがある。
m g は、球の重力落下による力であり、
m α は、腰の回転で加える水平方向の力加減と定義すると、
垂直応力の合計は、
N = r  μ m ( g cos Θ + α sin Θ)

よって、角運動方程式は、
I ω’(t) = r μ m (g cos Θ + α sin Θ)

擦った距離で積分すると、
∫I ω' r ω dt = N ∫v_Θ dt

ここに、μ ラバーの滑り係数
∫I ω’ r ω dt = r μ m (g cos Θ + α sin Θ) ∫v_Θ dt
I/2 ω² = μ m (g cos Θ + α sin Θ) v_Θ t

v_Θは、ラケットを球に当てる為の同期速度として定義するもので、
落下速度v_gで落下してくる球を、ラケットを振り抜き速度v_Θ振り下ろして当てる時、球をラケットで当てる垂直方向の空間の広さは、振り抜き角度のsinΘに比例する。当然、空間の広くなればラケット速度を上げるて大きくスイング出来るし、空間が狭ければラケット速度を下げて当てる様に小さくスイングする。
このことからラケットの振り抜き速度v_Θは球の落下速度v_gにk sinΘを乗じたものと考える。
kはスイング速度と落下速度との比でスイングの力加減とし、

v_Θ　= k sin Θ v_g
なので、ここではk = 1と考えると、

I/2 ω² = μ m (g cos Θ + α sin Θ) sin Θ v_g t

K_Θ = I/2 ω²と置くと
K_Θ = μ m (g cosΘ + α sin Θ) sin Θ v_g t

以下に、ラケット角度の振り抜き角度　Θ45°を基準 "1" として、各角度との比を回転速度比率として比較する。
例えば、Θ30°では、速度比率はK_Θ30°/ K_Θ45°となる。

(A) 鉛直力のみを垂直応力に課した場合

鉛直力 m g cos Θ のみを垂直応力N に課した場合を青色のグラフで示した。
振り抜き角度が小さい時、すなわち、ラケットを水平にする時、垂直応力は最大となり、反対に同期速度は最小になる。
また、ラケットを垂直にする時、垂直応力は最小になり、反対に同期速度は最大になる。
振り抜き角度はΘ45°でエネルギー量は最大値をとり、以下のグラフとなる。

一流のプロのスイングを確認して欲しい。彼らは、強い下回転スピンを出す時、次に述べる「ラケットの掴み方」で大体45°でラケットを振り下ろして球を擦っている。

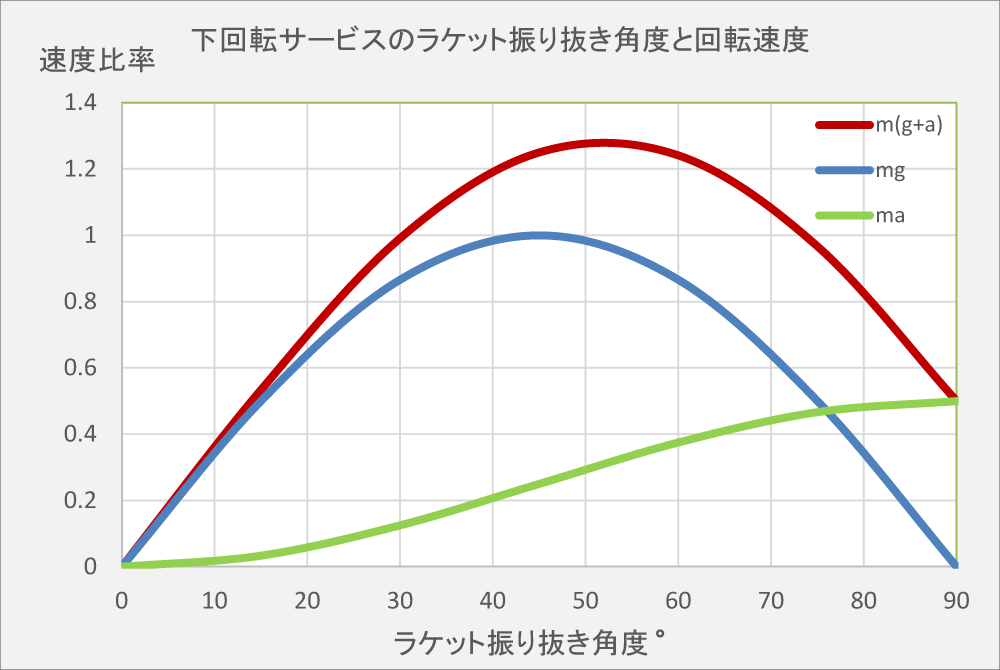
(B) 水平力のみを垂直応力に課した場合

水平力 m α sin Θ のみを垂直応力N に課した場合を黄緑色のグラフで示した。
ここでは、ラケットを垂直にして腰のみの回転で、αは0.25gとして振った時だ。何故、0.25gか、それは45°に強くラケットを振り下ろし、そして腰を回転させる時、スイングの振り始めから振り終わりまでの距離を１とした時に、腰の回転部分の距離は1/4程度となるからだ。

(C) 鉛直力と水平力とを垂直応力として課した場合

鉛直力 m g cos Θ と水平力 m α sin Θ とを垂直応力 N に課した場合を赤色のグラフで示した。すなわち、腰で回転させなが球に圧力を加えながらラケットを強く振り下ろした時に該当する。
振り抜き角度Θの最大値は、腰を回転しない時と比べ、４５°よりも若干立てることになるが、大よそ４０～６０°で最大ををとり、単に４５°の角度で振り下ろすよりも1.25倍の回転を与えることが出来る。

もどる

4.8.2 球の回転速度

振り抜き角度の評価にエネルギー量を用いたが、実際にサーブで必要なのは、球がラケットから離れる際の回転速度を速めることだ。

運動方程式は以下の通りだった。
I ω’(t) = N
I ω’(t) = r μ m (g cos Θ + α sin Θ) v_Θ'

擦った時間で積分すると、
∫I ω' dt = r μ m (g cos Θ + α sin Θ)∫^t ₀ v_Θ' dt
I ω = r μ m (g cos Θ + α sin Θ) (v_Θ(t) - v₀)

v₀ = 0 とすると、
I ω = r μ m (g cos Θ + α sin Θ) v_Θ(t)

運動方程式は加速を時間で足し合した面積が速度だと言っている。だから、回転速度を上げる為には、球をラケットで擦る間は速度を一定に振り抜くのではなくて、加速度 v_Θ' を保ち続けることが大切なのだ。

もどる

4.8.3 ラケットの振り方

サーブにおいて、下回転を強く掛ける時は、ラケットのグリップは遊びが無いようにシッカリと握る。球を、ラケットで擦る距離を最大になるようにラケットのグリップの根元から先端まで球を転がす様に45°程度の角度を保ち加速し続けて振り抜く。そして腰の回転で球に圧力を掛ける様に振り抜く。

フォア面の掴み

バック面の掴み

もどる