2.12 左利きへの対策
左利きは日本人の人口の10パーセント位らしい。右利きにとっては殆どが右利きの相手だ、だから、10人の内の1人の対策は後回しになる。 しかし左利きにとっては10人の内の9人は日常に違いない。彼らは右利きに慣れているのだ。 したがって、右利きにとって、左利きに対して無防備に戦ったのでは圧倒的に不利なのだ。そこで考える。
左利きの相手は通常、自分から見て左側のコーナー近くで構える。
左利きと対峙する時、自分の立ち位置は相手とはネットに対して線対照の位置で構えるのが良い。これは自分をポジショニングで相手と対等に置くためだ。 あとは知識の差で勝ちにいく。
左利きに対して非日常な回転とは何か。
サーブの回転で言えば、
左利きへ繰り出される日常のサーブ回転はカーブ・ドライブなのだ。
それはシュート・ドライブが非日常のサーブなのだ。だから、その効果が大きい。
ラリーで言えば、右利きのフォアスイングの回転はカーブ・ドライブなので、
それに対するレシーブはシュート・ドライブがドライブ返球となる。
しかし、左利きのフォアスイングの回転はシュート・ドライブ回転なので、
それに対するレシーブはカーブ・ドライブがドライブ返球となる。
試して見るとよい。今まで苦労していた左利きに対して互角に戦えるようになるだろう。
ここでは、相手のスイングと同方向の回転を混ぜてサーブすることから、ベクトル表記では無効な回転(オレンジ色の破線)で、相手のスイングからマイナスしている。詳細は7.2節「スピン合成とベクトル表記の考察」を詳しく書いている。まだ、読んでない人は先に読んでおく必要がある。
2.12.1 左利きへのサーブ
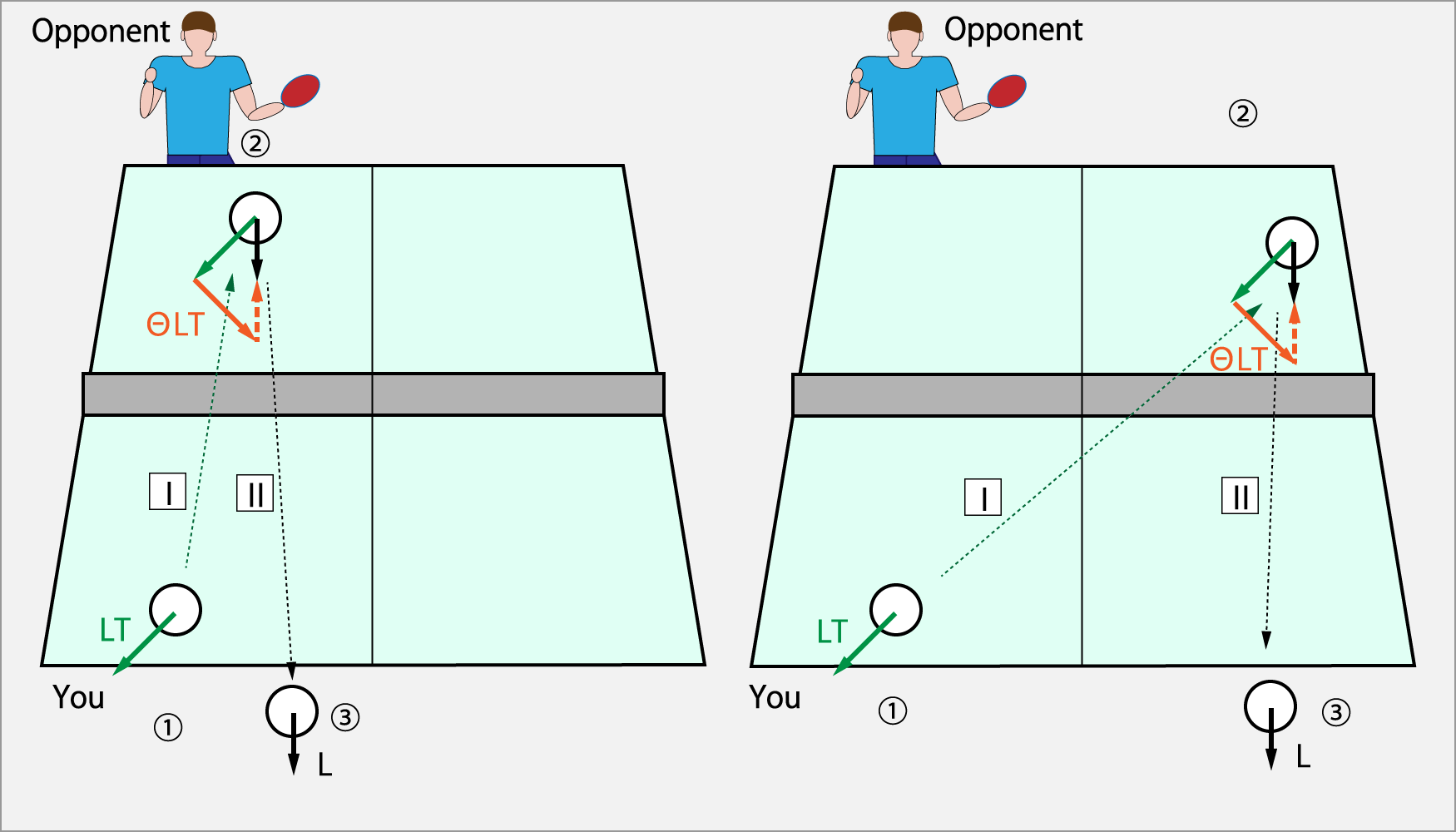
相手のミドルフォアへのサービス(左図)
① 相手のミドルフォアにシュート・ドライブ(LT)のサーブをする。
② 通常、左利きの相手は、Ⅰの回転をΘシュート・ドライブ(ΘLT)で受ける。
③ その結果、Ⅱのシュート(L)となってテーブルアウトする。
相手のフォアーへのサービス(右図)
① 相手のフォアにシュート・ドライブ(LT)のサーブをする。
② 通常、左利きの相手は、Ⅰの回転をΘシュート・ドライブ(ΘLT)で受ける。
③ その結果、Ⅱのシュート(L)となってテーブルアウトする。
方程式は以下の通りとなる。
シュート = Θシュート・ドライブ + シュート・ドライブ + カーブ
→ テーブルアウト
英語の頭文字で表記すると,
L = ΘLT + LT + R
2.12.2 左利きとラリー
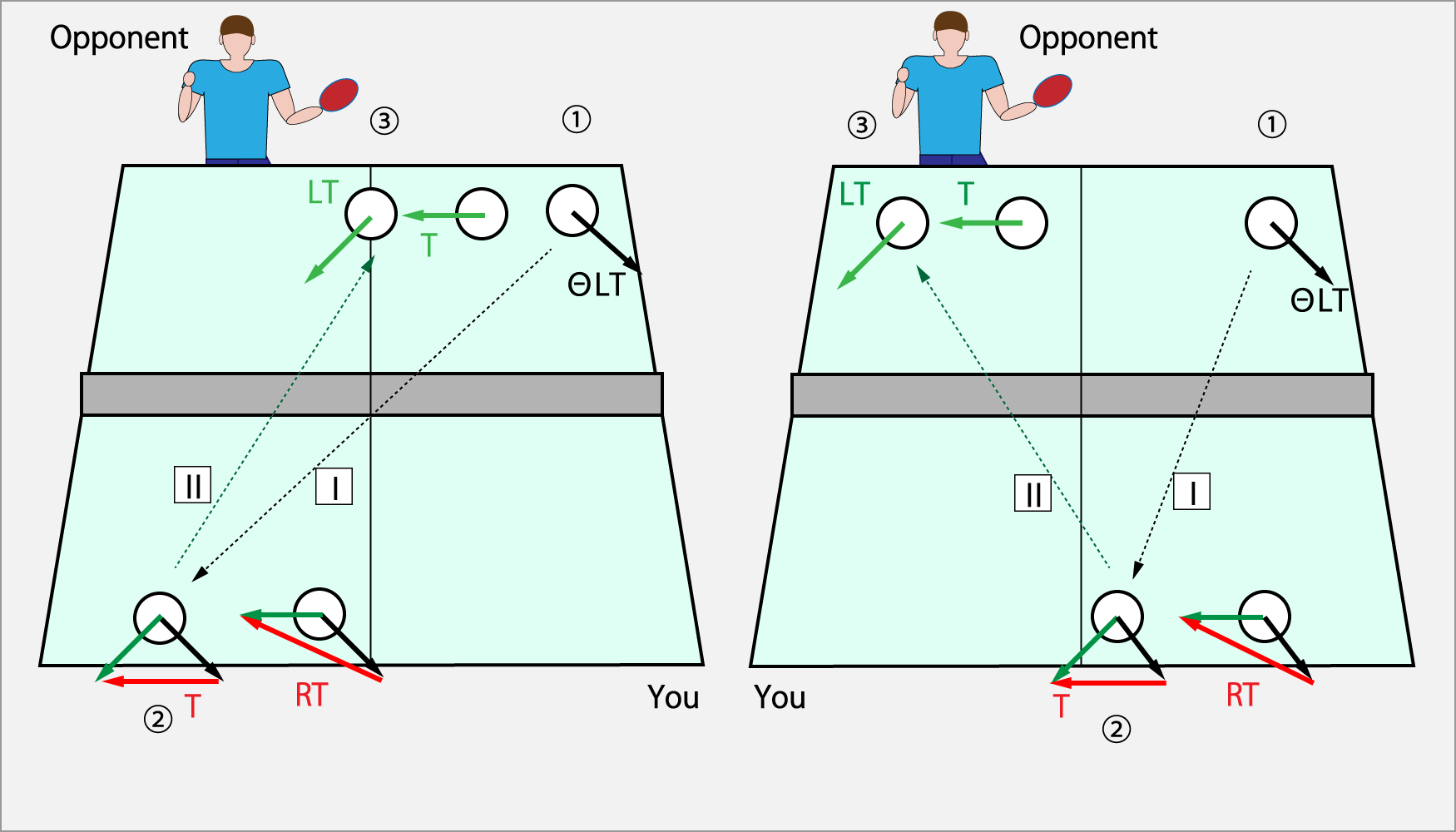
相手のフォア側へレシーブ(左図)
① 相手が無意識でフォアスイングするとΘシュート・ドライブ(ΘLT)で返球される。
② Ⅰの回転に対して、ドライブ(T)もしくはカーブ・ドライブ(RT)を加える。
③ その結果、Ⅱのシュート・ドライブ(LT)もしくはドライブ(T)となって送球される。
相手のバック側へレシーブ(右図)
① 相手が無意識でフォアスイングするとΘシュート・ドライブ(ΘLT)で返球される。
② Ⅰの回転に対して、ドライブ(T)もしくはカーブ・ドライブ(RT)を加える。
③ その結果、Ⅱのドライブ(T)もしくはシュート・ドライブ(LT)となって送球される。
方程式は以下の通りとなる。
シュート・ドライブ = Θシュート・ドライブ + ドライブ
英語の頭文字で表記すると,
LT = ΘLT + T
もしくは、
ドライブ = Θシュート・ドライブ + カーブ・ドライブ
英語の頭文字で表記すると,
T = ΘLT + RT