4.4 テーブルアウトを狙うサーブ

テーブルアウトを狙うサービスの回転には二通りある。

相手の振りによって球の回転軸を立てて横回転となるようサーブ回転を与えて打球の飛距離を伸ばす方法。

相手の振りと同方向の回転を与え、球の回転への力の寄与をなくし、その力で球の飛距離を伸ばしてしまう方法。

そして、相手のラケットヘッドの方向が下向きなのか上向きなのかで、長いサーブに対する相手のレシーブ回転の方向を予測することは容易だ。
ここでは相手の振りによって球の回転軸を立てて横回転としてしまう方法について説明しよう。

ベクトル表記では無効な回転(オレンジ色の破線)で、相手のスイングからマイナスしている。詳細は7.2節「スピン合成とベクトル表記の考察」を詳しく書いている。まだ、読んでない人は先に読んでおく必要がある。

4.4.1 ラケットヘッドを下げて振る相手へのサーブ

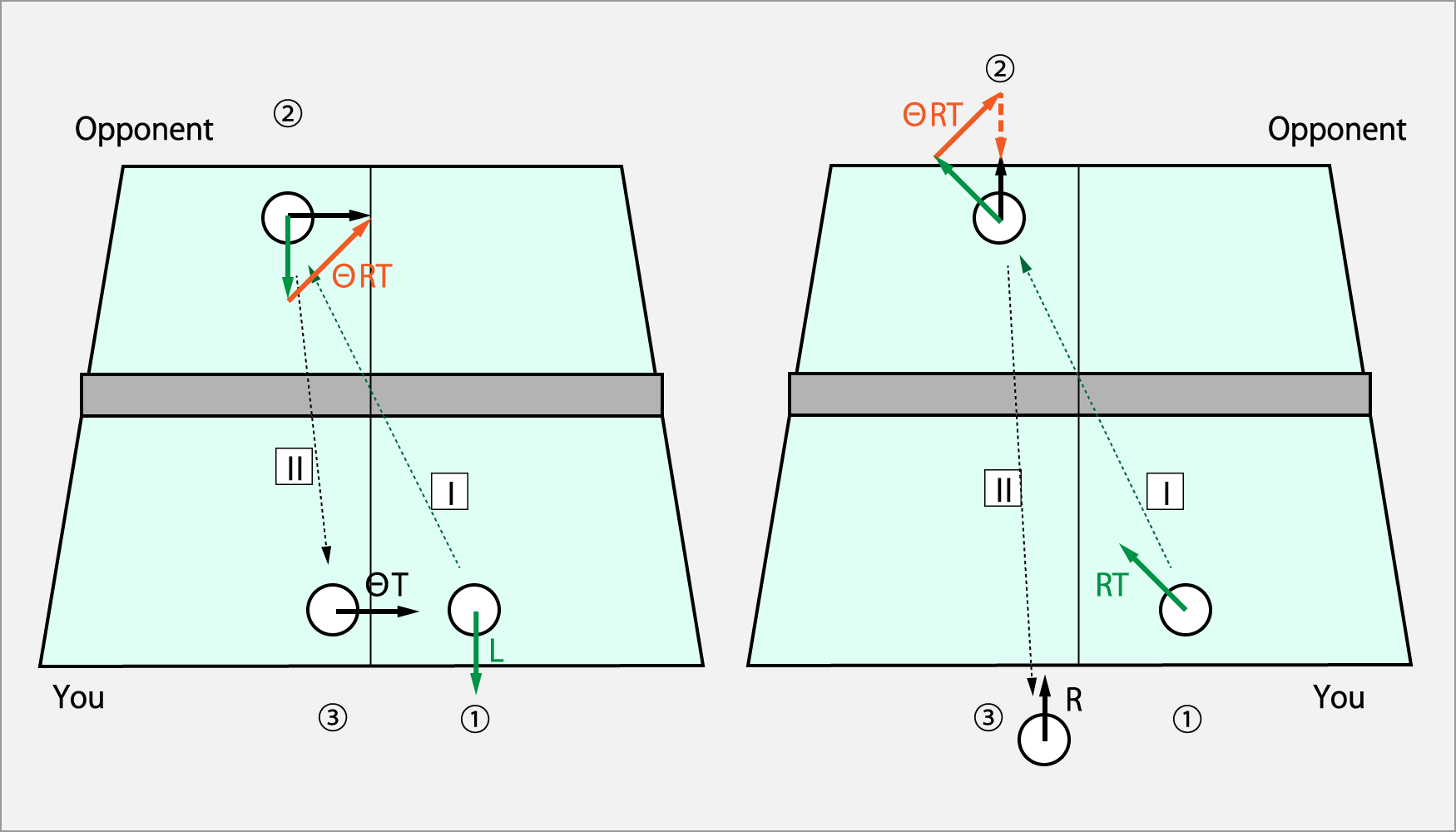
この図は、ラケットヘッドを下げて振リ始める相手(例えば、ラケットがペンフォルダーの相手とか、シェイクのドライブを得意な相手)に対して、君が繰り出すサーブを二つの回転方向を対比させ説明している。

左図は、シュート回転のサーブだ。
この回転の場合、ドライブとなって打ちこまれてしまう。

ラケットヘッドを下げての振りはΘカーブ・ドライブ(ΘRT)なのだ。

方程式は以下の通りとなる。
シュート　＋　Θカーブ・ドライブ　＝　Θドライブ　→　打ちこまれる

右図は、カーブ回転のサーブだ。
この回転の場合、球はフリスビーの様な回転で落ちることなくテーブルアウトになる。

方程式は以下の通りとなる。
カーブ・ドライブ　＋　　Θカーブ・ドライブ　－　シュート　＝　カーブ　→　フリスビー回転

テーブルアウトになってしまうことを知っている相手の場合は、つなぐレシーブをすることになるので、相手のレシーブをドライブで攻める。2.2 横回転をドライブで返球で攻める。

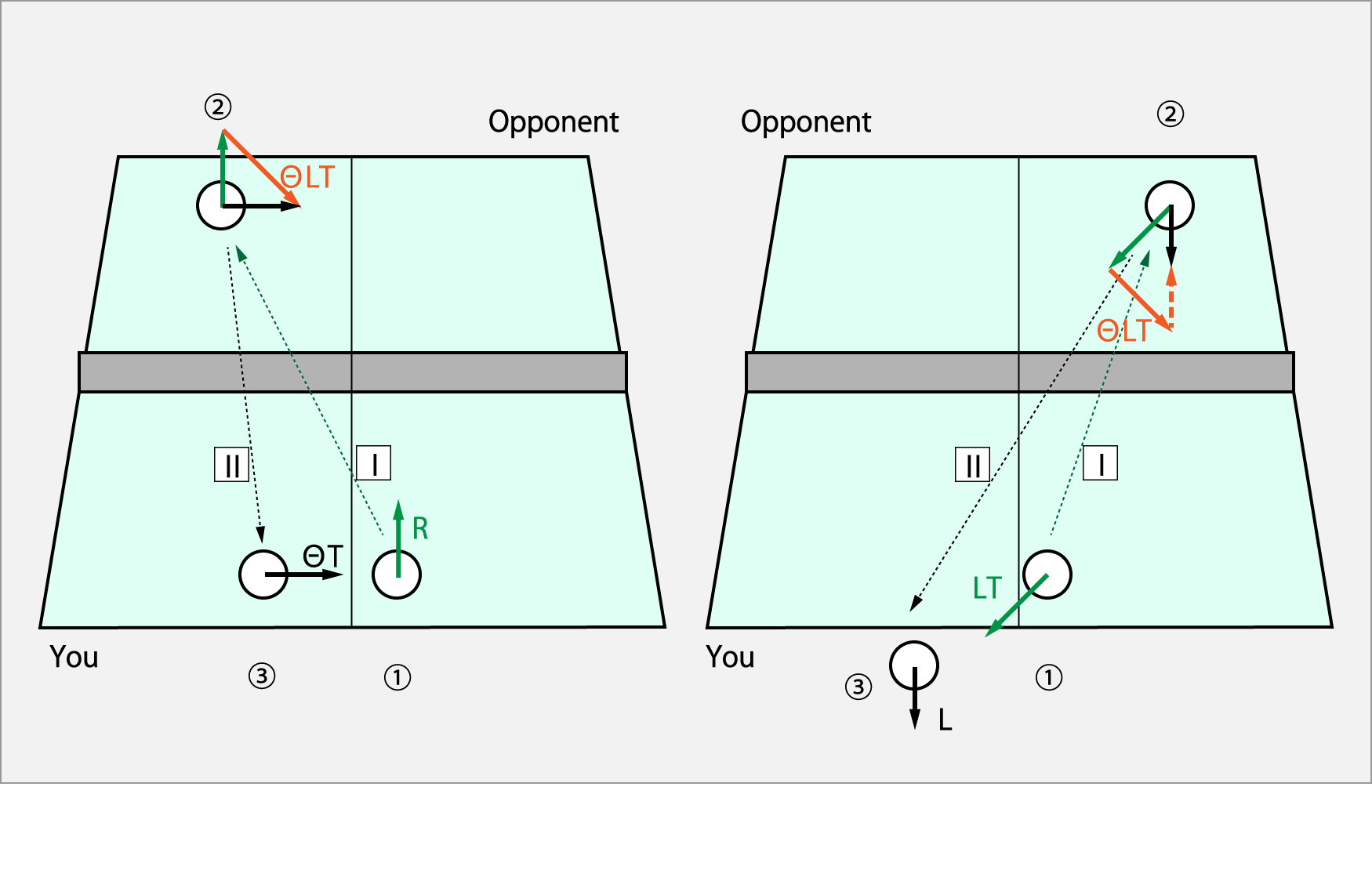
この図は、ラケットヘッドを上げて振リ始める相手に対して、君が繰り出すサーブを二つの回転方向を対比させ説明している。

左図は、カーブ回転(R)のサーブだ。
この回転の場合、ドライブとなって打ちこまれてしまう。

ラケットヘッドを上げての振りはΘシュート・ドライブ回転(ΘLT)なのだ。

方程式は以下の通りとなる。
カーブ　＋　Θシュート・ドライブ　＝　ドライブ　→　打ちこまれる

右図は、シュート回転(LT)のサーブだ。
この回転の場合、球はフリスビーの様な回転で落ちることなくテーブルアウトにすることが出来る。

シュート・ドライブ　＋　Θシュート・ドライブ－　カーブ　＝　シュート　→　フリスビー回転